CSC/ECE 506 Spring 2010/10 DJ
MEMORY CONSISTENCY MODELS
The interface[1] for memory in a shared memory multiprocessor is called a memory consistency model. The memory consistency model of a shared-memory multiprocessor provides a formal specification[3] of how the memory system will appear to the programmer, eliminating the gap between the behavior expected by the programmer and the actual behavior supported by a system.
SEQUENTIAL CONSISTENCY
Lamport[1] defined a multiprocessor to be Sequentially consistent [SC] if:
the result of any execution is the same as if the operations of all the processors were executed in some sequential order and the operations of each individual processor appear in this sequence in the order specified by the program.
The main advantage of selecting SC as the interface to shared memory hardware is that it is programmer’s intuition. SC permits coherence caching, prefetching and multithreading and yet keeps the software simple. In particular, SC enables middleware authors to use the same target as a multiprogrammed uniprocessor. Thus, SC should be a preferable choice for hardware architects.
Limitations of SC

Under SC, 1a -> 1b and 2a -> 2b. [2] So, in the above example A= 0 and B=0 never possible under SC.
1. A processor [3] must ensure that its previous memory operation is complete before proceeding with its next memory operation in program order. This requirement is called the program order requirement.
2. Determining [3] the completion of a write requires an explicit acknowledgement message from memory. Additionally, in a cache-based system, a write must generate invalidate or update messages for all cached copies.
3, SC makes it hard to use write buffers [1],because write buffers cause operations to be presented to the cache coherence protocol out of program order.
4. Some processors are precluded from overlapping multiple reads and writes in the memory system. This restriction is crippling in systems without caches.
5. Out of order execution [4] and instruction level parallelism can’t be used under SC.
6. Bypassing [4] a store to a younger load value is not allowed under SC since it violates atomicity.
7. Also, non blocking caches are not allowed.
8. For compilers [3], an analog of the program order requirement applies to straightforward implementations.
INTUITION behind relaxed memory-consistency models
After observing the limitations of SC, we conclude that the performance suffers greatly. The key idea will be to make execution of memory accesses faster and allow overlapping.
One possible solution is prefetching [4] When the older (previous) load/store is completed the load which has already issued a prefetch can access the cache and complete sooner because of cache hit. Also, when a store’s address is generated, a prefetch exclusive can be issued even though there are older pending load/stores. When these older loads/stores complete, the store can access the cache and complete without going to the bus.
After a block is been prefetched into the cache, it can be invalidated or after a block is prefetched in exclusive state, another processor may read, downgrading state to shared.
So, prefetches are useless because the load will suffer a cache miss and store with still need to go the bus. They also incur unnecessary traffic. hence, it is not a perfect solution.
Next possible solution is speculation[4] With speculation, a younger (later) load is allowed to access the cache, but marked as speculative. If, by the time the first load completes and the block read by the second load has not been invalidated or naturally evicted, then the value obtained by the second load would be same, if it had to wait for the first load to be executed atomically. So, speculation is successful, if it fails, cancel the younger load and re execute it. Also, a younger load can be speculative to an older pending store.
However, applying it to store is harder since it cannot be cancelled easily.
Both these techniques have been used in MIPS R10000 and Intel Pentium architecture.
Still, the compiler cannot re order memory accesses when compiling the program. Welcome relaxed memory consistency models.
RELAXED CONSISTENCY MODELS
Relaxed memory consistency models[3] can be categorized based on three key characteristics: (1) how they relax the program order requirement, i.e.: whether they relax the order from a write to a following read, between two writes, and finally from a read to a following read or write and (2) how they relax the write atomicity requirement, i.e: whether they allow a read to return the value of another processor’s write before the write is made visible to all other processors.(3) A relaxation to both program order and write atomicity, where a processor is allowed to read the value of its own previous write before the write is made visible to other processors. In a cache-based system, this relaxation allows the read to return the value of the write before the write is serialized with respect to other writes to the same location and before the invalidations/updates of the write reach any other processor.
| Relaxation | Commercial Systems Providing the Relaxation |
| W -> R Order | AlphaServer 8200/8400, Cray T3D, Sequent Balance, SparcCenter1000/2000 |
| W -> W Order | AlphaServer 8200/8400, Cray T3D |
| R -> RW Order | AlphaServer 8200/8400, Cray T3D |
| Read Others’ Write Early | Cray T3D |
| Read Own Write Early | AlphaServer 8200/8400, Cray T3D, SparcCenter1000/2000 |
Relaxing the WRITE to READ Program Order
Here, the program orders are relaxed for a write followed by a read to a different location. These models [3] include the IBM370model, the SPARC V8 TSO and the processor consistency model (PC) .These models allow a read to be reordered with respect to previous writes from the same processor.
IBM 370
It is the strictest because it does not allow a read from returning the value of a write before the write is made visible to all processors. Therefore, even if a processor issues a read to the same address as a previous pending write from itself, the read must be delayed until the write is made visible to all processors.
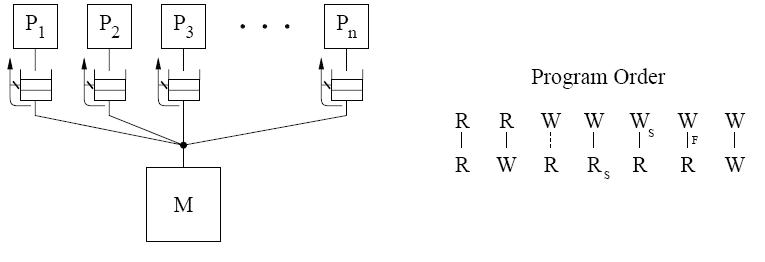
Here, Rs & Ws mean read and write generated by serialization instructions.
Dashed lines indicate in program order.
To ensure the program order constraint, it provides special serialization instructions that may be placed between the two operations. eg. compare&swap.

Placing a serialization instruction after the write on each processor provides sequentially consistent results.
It does not need a safety net to ensure atomicity since it does not relax atomicity.
TSO model
The total store ordering (TSO) model is one of the models proposed for the SPARC V8 architecture [SFC91,SUN91].
It allows a read to return the value of its own processor’s write even before the write is serialized with respect to other writes to the same location.
It requires that no other writes to any location appear to occur between the read and the write of the read-modify-write.
It does not provide explicit safety nets.
The atomicity can be achieved by ensuring program order from the write to the read using read-modify-writes.
The disadvantages to rely on a read-modify write as a safety net:
A system may not implement a general read-modify-write that can be used to appropriately replace any read or write and replacing a read by a read-modify-write needs invalidating other copies of the line.
PC model
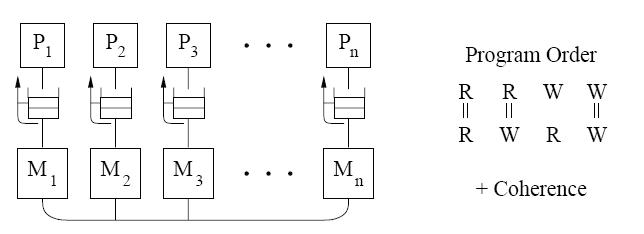
Double lines[6] between reads/writes denote the fact that operations may no longer be atomic and that all sub-operations of the first operation must complete before any sub-operations of the second operation.
PC relaxes both constraints, such that a read can return the value of any write before the write is serialized or made visible to other processors.
It requires that no other writes to the same location appear to occur between the read and the write of the read-modify-write.
The program order between a write and a following read appears to be maintained if the read is replaced by or is already part of a read-modify-write.
They do not provide explicit safety nets.
A write is guaranteed to appear atomic if every read that may return the value of the write is part of, or replaced with, a read-modify-write.
However, it has the same disadvantage of TSO for relying on read-modify-write.

PC is less useful than the others, because it does not guarantee a property called causality. Causality requires that all other processors see the effect of a processor’s operation when any other processor sees it. Without causality, processor consistency can fail to look like SC in important cases involving three or more processors.
Relaxing the WRITE to READ and WRITE to WRITE Program Orders
The partial store ordering model (PSO)[3] is an extension of the TSO model and is the second model provided by the SPARC V8 architecture.
As far as atomicity is concerned, it is same as TSO.
PSO provides an explicit STBAR instruction for imposing program order between two writes.
However, PSO is still not good enough to be useful to a compiler.
Relaxing all program orders
The program order [3] between all operations to different locations is relaxed. Thus, a read or write operation may be reordered with respect to a following read or write to a different location.
Examples of such models are: weak ordering(WO) model, release consistency models (RCsc/RCpc), and three models proposed for commercial architectures: the Digital Alpha, SPARC V9 relaxed memory order (RMO), and IBM PowerPC models.
All the above models allow memory operations following a read operation to be overlapped or reordered with respect to the read operation.In hardware, this flexibility provides the possibility of hiding the latency of read operations.
All of the models in this group allow a processor to read its own write early.
RCpc and PowerPC are the only models whose straightforward implementations allow a read to return the value of another processor’s write early.Except for Alpha, all the above models allow the reordering of two reads to the same location.
Complex implementations of RCsc can potentially violate atomicity such that it can affect the result of a program.
The WO, RCsc, and RCpc models distinguish memory operations based on their type, and provide stricter ordering constraints for some types of operations. On the other hand, the Alpha, RMO, and PowerPC models provide explicit fence instructions for imposing program orders between various memory operations.
WEAK ORDERING
The weak ordering model (also known as weak consistency) was proposed by Dubois et al. [DSB86][6] and relies on maintaining program order only at the synchronization points in the program.
Many programs use synchronization to make sure data is up-to-date and programs to do not exhibit nondeterministic behavior. The synchronization primitive will ensure that all previous instructions before the synchronization primitive have executed and committed to memory before the current instruction is executed.

Rs and Ws denote read and write identified as synchronization.
Triple lines denotes that the read sub-operation and the sub-operations of the write (possibly from a different processor) whose value is returned by the read should complete before any of the sub-operations of the operation that follows the read in program order.
The weak ordering model assumes that 1) programs are properly synchronized and that 2) synchronization is supported by the hardware.
Also, assumptions about the synchronization primitives are that 1) before synchronization, all prior loads, stores, and synchronizations must have been completed and 2) all loads, stores, synchronizations following must not have been issued yet.
With these assumptions, the weak ordering model can be used. The weak ordering model allows memory accesses between synchronization points to be reordered.
The following illustration shows how this model is used.
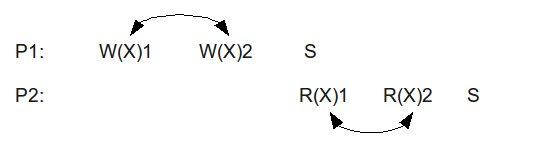
With weak ordering memory operations between synchronization points can be reordered. This means that W(X)1 and W(X)2 can be reordered before the synchronization point. In fact, W(X)1 and W(X)2 may not even have been fully committed to memory prior to the synchronization point. As long as all of the operations executed and commit to memory before the synchronization, weak ordering is satisfied. Similarly, the read operations of P2 can also be reordered. Weak ordering, however, does not allow reordering to occur across synchronization points, as illustrated in the figure below.
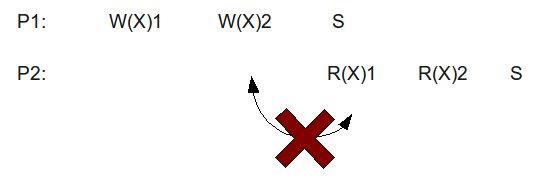
The R(X)1 and W(X)2 across synchronization points cannot be reordered, otherwise it would violate weak ordering and would lead to non-deterministic results.
Several synchronization[4] mechanisms can be used including barriers, fences, fetch-and-op, test-and-set, load linked and store conditional, and so on. The synchronization mechanisms must ensure that instructions stall until all prior loads and stores complete and propagate.Compared to SC, WO provides better performance since memory operations can be reordered between synchronization points. Compared to PC, WO typically gives better performance. However, when there are several synchronization points, limiting reordering potential, PC may achieve better performance.
RELEASE CONSISTENCY
Release consistency is similar to weak ordering, but it can relax the model even further by distinguishing between the two types of synchronization: acquisition and release. In programs, some thread will produce some data, and another thread will consume it. The consuming thread cannot run before the producing thread. Looking at the same code from before, it is clear that P0 is the producer and P1 is the consumer.
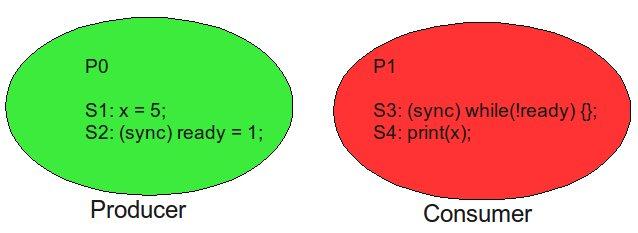
From the weak ordering model, when we encounter an 'S' instruction, or synchronization point, here is what happens.
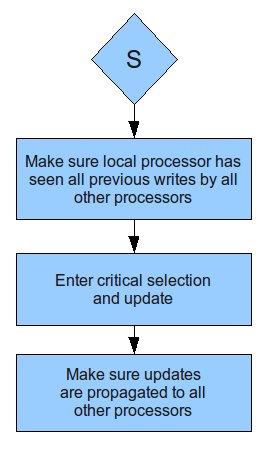
Looking at the code above the producer P0 upon encountering the synchronization instruction will make sure to see previous writes by other processors, enter critical selection and update ready, then propagate to other processors.The consumer P1, upon encountering the synchronization point will make sure to see previous by other processors, enter critical selection and read ready, then propagate to other processors.
Notice that both the consumer and producer perform redundant operations. The producer does not need to see previous writes from other processors because it doesn't read any values! Similarly, the consumer does not need to propagate updates to other processors because it never made any updates.
The release consistency model addresses this problem by distinguishing synchronization points for both producer and consumer. The producer synchronization is called a release and the consumer synchronization is called an acquisition.
Here are the procedures for release and acquisition
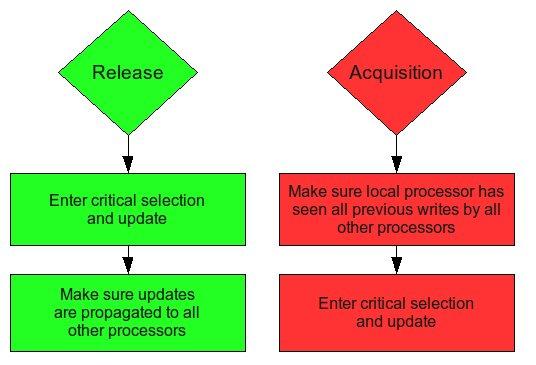
By definition of release consistency, an acquisition must ensure that following load and stores must not executed until acquisition is complete. Also, a release must ensure that previous load and stores must complete before release. The following diagram shows release consistency in action.

There are two flavors[6] of release consistency that differ in the order that is maintained among synchronization operations. The first flavor maintains sequential consistency among synchronization operations and is referred to RCsc, while the second flavor maintains processor consistency among such operations and is called RCpc. Except for the program order requirements, these two models are identical.

Similar to WO, RC requires that programs are synchronized correctly. In addition, the synchronizations must be labeled as either an acquisition or release. This obviously increases programming complexity. By reducing redundant operations, the performance of release is better than WO. This performance increase, however, may be overshadowed by the additional cost of programming complexity in identifying which synchronizations are release or acquisition.
Comparing RC and WO
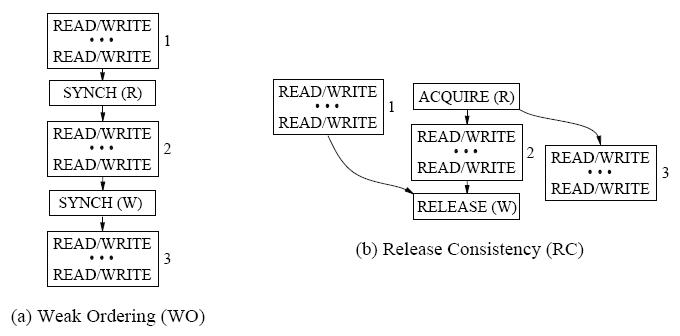
RC allows for extra reordering and overlap of memory operations across acquires and releases.
Alpha, RMO, and PowerPC
The Alpha, RMO, and PowerPC models all provide explicit fence instructions as their safety nets.[3]
Alpha model
The Alpha model provides two different fence instructions, the memory barrier (MB) and the write memory barrier (WMB). The MB instruction can be used to maintain program order from any memory operations before the MB to any memory operations after the MB. The WMB instruction provides this guarantee only among write operations.

An MB imposes program order between all read and write operations, while the WMB only imposes program order between writes. Finally, memory operations to the same location, including reads to the same location, are required to complete in program order.
SC can be guaranteed[6] by naively placing a fence instruction between any pair of memory operations. Similarly, we can preserve the requirements for WO by placing a fence instruction before and after every memory operation identified as a synchronization.
SPARC V9 Relaxed Memory Order (RMO)
The relaxed memory order (RMO)[6] model is an extension of the TSO and PSO models and was adopted for the SPARC V9 architecture [WG94]. RMO extends the PSO model to allow a read to complete out of program order with respect to following read and write operations.

RMO provides four types of fences that allow program order to be selectively maintained between any two types of operations. A single fence instruction can specify a combination of the above fence types by setting the appropriate bits in a four-bit opcode.
A MEMBAR[3] instruction can be customized to order a combination of previous read and write operations with respect to future read and write operations. The fact that a MEMBAR can be used to order a write with respect to a following read alleviates the need for using read-modify-writes to achieve this order, as is required in the SPARC V8 TSO or PSO models.
IBM PowerPC model

The IBM PowerPC model exposes the multiple-copy semantics[6] of memory to the programmer. PowerPC provides a single fence instruction, called a SYNC, that may be used to impose program orders. For imposing program order[3], the SYNC instruction behaves similar to the MB instruction of the Alpha model with the exception that even if a SYNC is placed between two reads to the same location, it is possible for the second read to return the value of an older write than the first read; i.e., the reads appear to occur out of program order. This can create subtle correctness problems in programs, and may require the use of read-modify-write operations.(analogous to their use for PC and RCpc) to enforce program order between two reads to the same location. PowerPC allows a write to be seen early by another processor’s read; therefore, read-modify-write operations may need to be used to make a write appear atomic. Read forwarding from the buffer are actually safe.
Here is a summary of relaxed models
| Relaxation | W-> R order | W -> W order | R -> RW order | Read Others Write Early Order | Read Own Write Early Order | Safety net |
| SC | Y | |||||
| IBM 370 | Y | serialization instructions | ||||
| Total Store Ordering | Y | Y | RMW | |||
| PC | Y | Y | Y | RMW | ||
| PSO | Y | Y | Y | RMW, STBAR | ||
| WO | Y | Y | Y | Y | synchronization | |
| RCsc | Y | Y | Y | Y | release, acquire, nsync, RMW | |
| RCpc | Y | Y | Y | Y | Y | release, acquire, nsync, RMW |
| Alpha | Y | Y | Y | Y | MB, WMB | |
| RMO | Y | Y | Y | Y | MEMBARs | |
| PowerPC | Y | Y | Y | Y | Y | Sync |
Y: corresponding relaxation is allowed by straightforward implementations of the corresponding model & can be detected by the programmer
LAZY Consistency
Further optimizations to the RC model are possible. When an A(L) or acquisition instruction is encountered we don't need the updated values from other processors immediately until sometime after the A(L) instruction. This allows the release to be delayed or "lazy." The release values are also clumped together so all of the modified values needed are sent in one pack. The following is illustrated below.
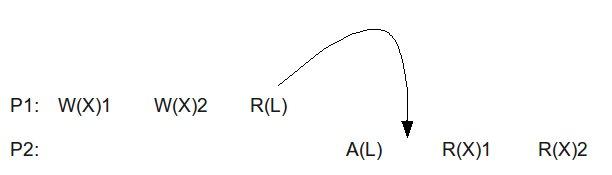
Instead of acquiring at the A(L) instruction, it is delayed until after. Also, changes to memory addresses 1 and 2 are sent together. This model allows more time for release and reduces memory traffic by propagating changes together in one group. Changes in RC model to support delaying the release are necessary. LRC is not employed in hardware supported cache coherent systems.
Delaying the release and grouping the releases together may cause additional latency on the subsequent acquire. However, with lazy consistency the number of writes is reduced and performance may improve on systems that high memory overheads.
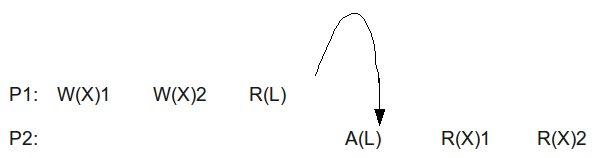
EAGER Consistency
The difference between eager release and lazy release, is that eager release performs updates immediately upon release. Unlike lazy consistency, which delays updates until after subsequent acquire, the eager release will perform updates immediately. The following illustrates the procedure.
Performance of Eager v/s Lazy Consistency
Lazy consistency bundles memory operations together after release, so that unnecessary memory operations such as invalidations can be avoided. This can improve the performance of a program by reducing the memory contention and number of transactions. On the other hand, by delaying the release, the latency of the synchronization may increase. Eager release consistency performs the synchronization immediately, reducing the synchronization delay time. However, eager release may cause higher memory contention. The following graph depicts an experiment run by Kontothanassis et. al. at the University of Rochester, where the performance of eager and lazy consistencies were compared on different sets of data.
The results show that lazy release consistency has better performance in nearly all of the tests. The advantage of the lazy protocol here stems from the reduction of memory contention and the elimination of redundant memory hops, which leads to overall better performance.
Compiler Optimizations
In WO, RCsc and RCpc models, the compiler[3] has the flexibility to reorder memory operations between two consecutive synchronization or special operations. Similarly, in the Alpha, RMO, and PowerPC models, the compiler has full flexibility to reorder operations between consecutive fence instructions. Since most programs use these operations or instructions infrequently, the compiler gets large regions of code where virtually all optimizations that are used for uniprocessor programs can be safely applied.
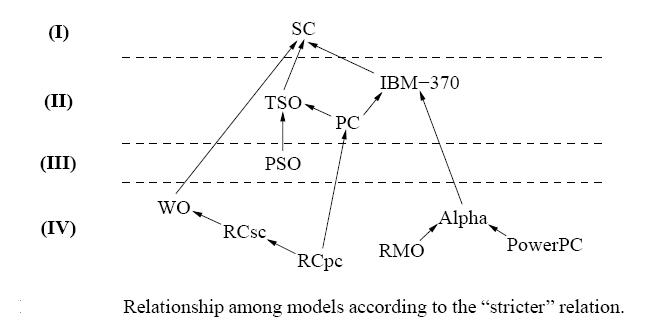
Below is the comparison of the relaxed consistency models. Level I being the strictest and Level IV being the most relaxed