CSC/ECE 506 Spring 2010/12 EC: Difference between revisions

From Expertiza_Wiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 24: Line 24:
'''Linear Array'''
'''Linear Array'''
<p>
<p>
<pic top_linear>
[[Image:Top_linear.jpg]]
<br>
<br>
The nodes are connected linearly as in an array. This type of topology is simple, however, it does not scale well. The longest distance between two nodes, or the '''diameter''', is equivalent to the number of nodes.  
The nodes are connected linearly as in an array. This type of topology is simple, however, it does not scale well. The longest distance between two nodes, or the '''diameter''', is equivalent to the number of nodes.  
</p>
</p>
Line 31: Line 33:
'''Ring'''
'''Ring'''
<p>
<p>
<pic top_ring>
[[Image:Top_ring.jpg]]
<br>
<br>
Similar structure as the linear array, except, the ending nodes connect to each other, establishing a circular structure. The longest distance between two nodes is cut in half.
Similar structure as the linear array, except, the ending nodes connect to each other, establishing a circular structure. The longest distance between two nodes is cut in half.
</p>
</p>
Line 38: Line 42:
'''2-D Mesh'''
'''2-D Mesh'''
<p>
<p>
<pic top_2Dmesh>
[[Image:Top_2Dmesh.jpg]]
<br>
<br>
The 2-D mesh can be thought of as several linear arrays put together to form a 2-dimensional structure. Nodes that are not on the edge have 4 input or output links, or a '''degree''' of 4.
The 2-D mesh can be thought of as several linear arrays put together to form a 2-dimensional structure. Nodes that are not on the edge have 4 input or output links, or a '''degree''' of 4.
</p>
</p>
Line 45: Line 51:
'''2-D Torus'''
'''2-D Torus'''
<p>
<p>
<pic top_2Dtorus>
[[Image:Top_2DTorus.jpg]]
<br>
<br>
The 2-D torus takes the structure of the 2-D mesh and connects the nodes on the edges. This decreases the diameter, but the number of links is higher.  
The 2-D torus takes the structure of the 2-D mesh and connects the nodes on the edges. This decreases the diameter, but the number of links is higher.  
</p>
</p>
Line 52: Line 60:
'''Cube'''
'''Cube'''
<p>
<p>
<pic top_cube>
[[Image:Top_cube.jpg]]
<br>
<br>
The cube can be thought of as a three-dimensional mesh.
The cube can be thought of as a three-dimensional mesh.
</p>
</p>
Line 59: Line 69:
'''Hypercube'''
'''Hypercube'''
<p>
<p>
<pic top_hypercube>
[[Image:Top_hypercube.jpg]]
<br>
<br>
The hypercube is essentially multiple cubes put together.
The hypercube is essentially multiple cubes put together.
</p>
</p>
Line 66: Line 78:
'''Tree'''
'''Tree'''
<p>
<p>
<pic top_tree>
[[Image:Top_tree.jpg]]
<br>
<br>
The tree is a hierarchical structure nodes on the bottom and switching nodes at the upper levels. The tree experiences high traffic at the upper levels.  
The tree is a hierarchical structure nodes on the bottom and switching nodes at the upper levels. The tree experiences high traffic at the upper levels.  
</p>
</p>
Line 73: Line 87:
'''Fat Tree'''
'''Fat Tree'''
<p>
<p>
<pic top_fat_tree>
[[Image:Top_fat_tree.jpg]]
<br>
<br>
The fat tree alleviates the traffic at upper levels by "fattening" up the links at the upper levels.  
The fat tree alleviates the traffic at upper levels by "fattening" up the links at the upper levels.  
</p>
</p>
Line 80: Line 96:
'''Butterfly'''
'''Butterfly'''
<p>
<p>
<pic top_butterfly>
[[Image:Top_butterfly.jpg]]
<br>
<br>
The butterfly structure is similar to the tree structure, but it replicates the switching node structure of the tree topology and connects them together so that there are equal links and routers at all levels.
The butterfly structure is similar to the tree structure, but it replicates the switching node structure of the tree topology and connects them together so that there are equal links and routers at all levels.
</p>
</p>
Line 102: Line 120:
<p>
<p>
The overall structure of the network is shown below. Note that this structure is very susceptible to failure and congestion.
The overall structure of the network is shown below. Note that this structure is very susceptible to failure and congestion.
 
<br>
<pic disknet_network>
[[Image:Disknet_network.jpg]]
<br>
</p>
</p>


Line 117: Line 136:
<p>
<p>
In high performance applications, the butterfly structure is a good choice. The butterfly topology uses fewer links than other topologies, however, each link carries traffic from the entire layer. Fault tolerance is poor. There exists only a single path between pairs of nodes. Should the link break, data cannot be re-routed, and communication is broken<sup>2</sup>.
In high performance applications, the butterfly structure is a good choice. The butterfly topology uses fewer links than other topologies, however, each link carries traffic from the entire layer. Fault tolerance is poor. There exists only a single path between pairs of nodes. Should the link break, data cannot be re-routed, and communication is broken<sup>2</sup>.
 
<br>
<pic disknet_butterfly>
[[Image:Disknet_butterfly.jpg]]
</p>
</p>
<br>
<br>
Line 125: Line 144:
<p>
<p>
The mesh and torus structure used in this application would require a large number of links and total aggregate of several thousands of ports. However, since there are so many links, the mesh and torus structures provide alternates paths in case of failures<sup>2</sup>.  
The mesh and torus structure used in this application would require a large number of links and total aggregate of several thousands of ports. However, since there are so many links, the mesh and torus structures provide alternates paths in case of failures<sup>2</sup>.  
 
<br>
<pic disknet_mesh>
[[Image:Disknet_mesh.jpg]]
<pic disknet_torus>
<br>
[[Image:Disknet_torus.jpg]]
</p>
</p>
<br>
<br>
Line 134: Line 154:
<p>
<p>
Similar to the torii structures, the hypercube requires larger number of links. However, the bandwidth scales better than mesh and torii structures.  
Similar to the torii structures, the hypercube requires larger number of links. However, the bandwidth scales better than mesh and torii structures.  
 
<br>
<pic disknet_hypercube>
[[Image:Disknet_hypercube.jpg]]
</p>
</p>
<br>
<br>

Revision as of 19:07, 22 April 2010

Interconnection Network Architecture

Introduction

In a multi-processor system, processors need to communicate with each other and access each other's resources. In order to route data and messages between processors, an interconnection architecture is needed.


Typically, in a multiprocessor system, message passed between processors are frequent and short1. Therefore, the interconnection network architecture must handle messages quickly by having low latency, and must handle several messages at a time and have high bandwidth.


In a network, a processor along with its cache and memory is considered a node. The physical wires that connect between them is called a link. The device that routes messages between nodes is called a router. The shape of the network, such as the number of links and routers, is called the network topology.


Types of Network Topologies

Linear Array



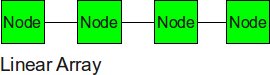
The nodes are connected linearly as in an array. This type of topology is simple, however, it does not scale well. The longest distance between two nodes, or the diameter, is equivalent to the number of nodes.


Ring



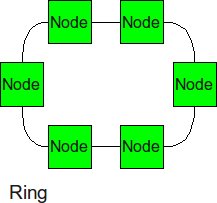
Similar structure as the linear array, except, the ending nodes connect to each other, establishing a circular structure. The longest distance between two nodes is cut in half.


2-D Mesh



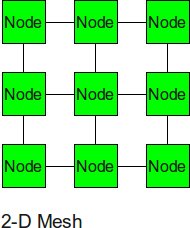
The 2-D mesh can be thought of as several linear arrays put together to form a 2-dimensional structure. Nodes that are not on the edge have 4 input or output links, or a degree of 4.


2-D Torus

File:Top 2DTorus.jpg

The 2-D torus takes the structure of the 2-D mesh and connects the nodes on the edges. This decreases the diameter, but the number of links is higher.


Cube



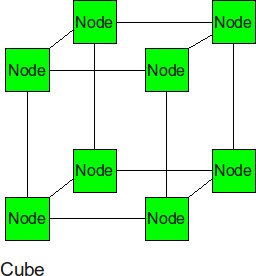
The cube can be thought of as a three-dimensional mesh.


Hypercube



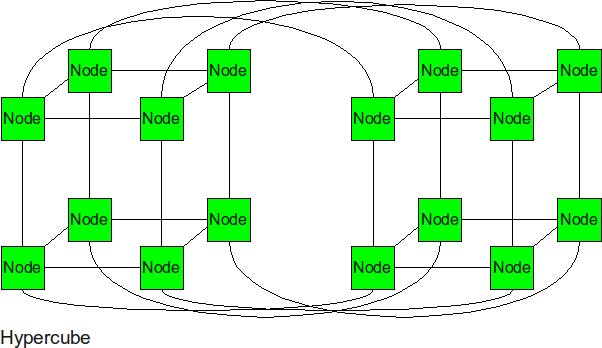
The hypercube is essentially multiple cubes put together.


Tree



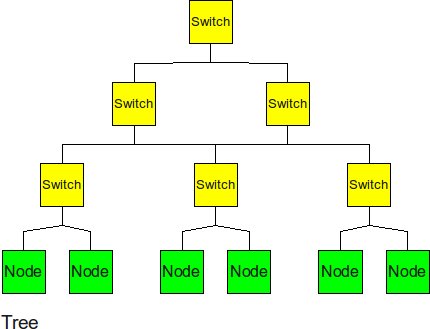
The tree is a hierarchical structure nodes on the bottom and switching nodes at the upper levels. The tree experiences high traffic at the upper levels.


Fat Tree



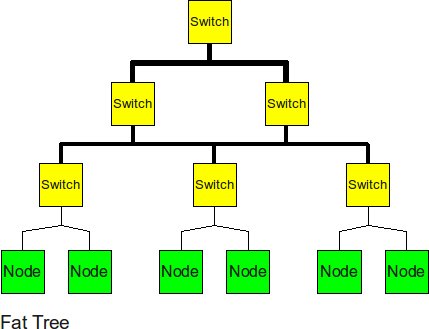
The fat tree alleviates the traffic at upper levels by "fattening" up the links at the upper levels.


Butterfly



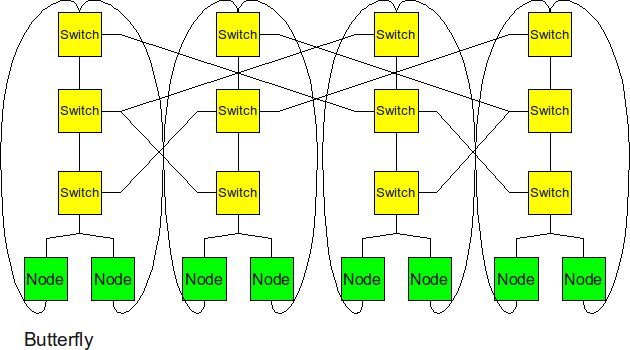
The butterfly structure is similar to the tree structure, but it replicates the switching node structure of the tree topology and connects them together so that there are equal links and routers at all levels.



Real-World Implementation of Network Topologies

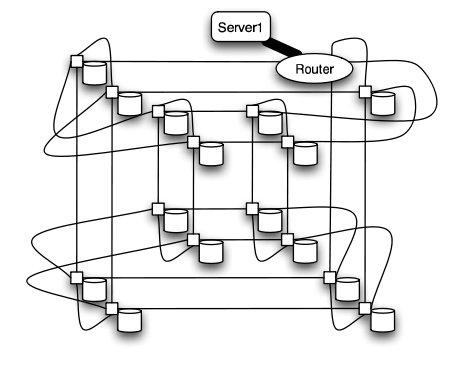
In a research study by Andy Hospodor and Ethan Miller, several network topologies were investigated in a high-performance, high-traffic network2. Several topologies were investigated including the fat tree, butterfly, mesh, torii, and hypercube structures. Advantages and disadvantages including cost, performance, and reliability were discussed.


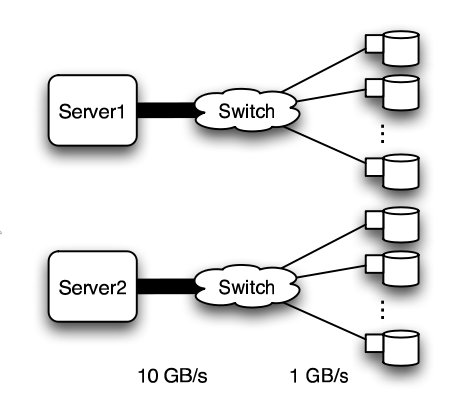
In this experiment, a petabyte-scale network with over 100 GB/s total aggregate bandwidth was investigated. The network consisted of 4096 disks with large servers with routers and switches in between2.


The overall structure of the network is shown below. Note that this structure is very susceptible to failure and congestion.


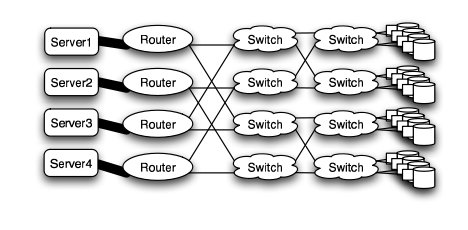
Fat Tree

In large scale, high performance applications, fat tree can be a choice. However, in order to "fatten" up the links, redundant connections must be used. Instead of using one link between switching nodes, several must be used. The problem with this is that with more input and output links, one would need routers with more input and output ports. Router with excess of 100 ports are difficult to build and expensive, so multiple routers would have to be stacked together. Still, the routers would be expensive and would require several of them2.


Butterfly

In high performance applications, the butterfly structure is a good choice. The butterfly topology uses fewer links than other topologies, however, each link carries traffic from the entire layer. Fault tolerance is poor. There exists only a single path between pairs of nodes. Should the link break, data cannot be re-routed, and communication is broken2.


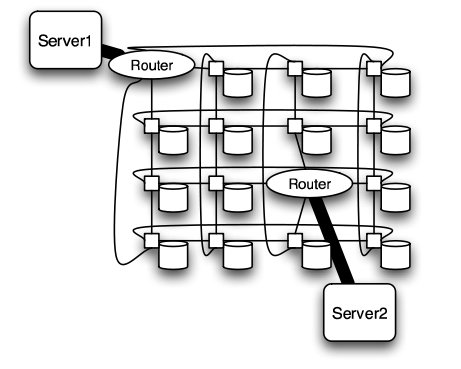
Meshes and Torii

The mesh and torus structure used in this application would require a large number of links and total aggregate of several thousands of ports. However, since there are so many links, the mesh and torus structures provide alternates paths in case of failures2.


Hypercube

Similar to the torii structures, the hypercube requires larger number of links. However, the bandwidth scales better than mesh and torii structures.


Retrieved from "https://wiki.expertiza.ncsu.edu/index.php?title=CSC/ECE_506_Spring_2010/12_EC&oldid=32208"