Chapter 4a: Brandon Chisholm, Chris Barile
Automatic Parallelism is the process of automatically converting sequential code into code that will make use of multiple processors. One main reason for implementing automatic parallelism is to save time and energy compared to converting the code manually.<ref name="wiki" /> There are several techniques that have been created for parallelizing code, but each has limitations.
Techniques
Profile-Driven Parallelism
This technique involves running the program while recording each memory access in detail. The memory accesses are then looked at to determine what code can be parallelized. This technique is simple, but does not cover all the possible input combinations. These may lead to false positives in which code segments can be labelled as parallelizeable when they actually aren't.<ref name="chia" />
Polyhedral Transformation
Polyhedral transformation involves representing loop iterations from the source code as lattice points in something called a polytope. This polytope is then transformed into a more optimized form. This approach is limited when pointers are found inside loops. The following pictures represent a polytope before and after the transformation.<ref name="chia" />
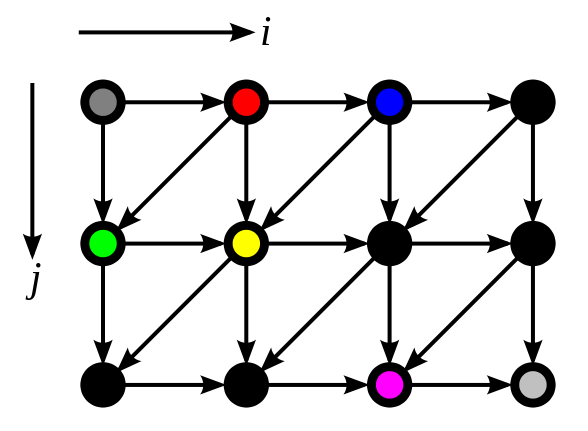
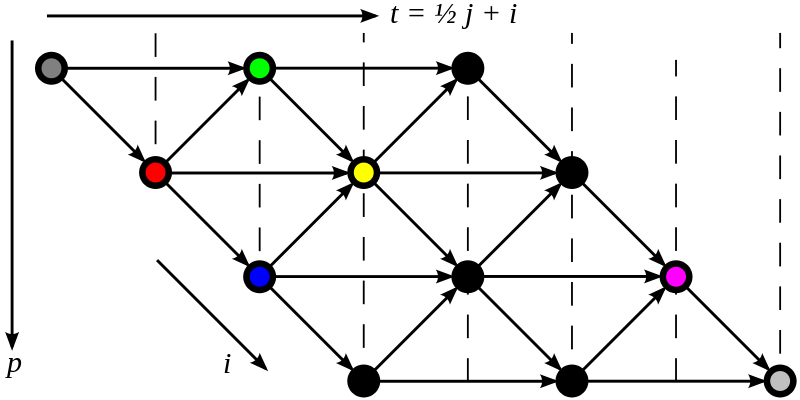
Automatic Program Exploration
Also known as "concolic execution", "mixed concrete and symbolic execution", or "symbolic execution", automatic program exploration is originally a bug finding technique that provides full coverage of the program. The first step in this approach is to symbolically represent the inputs to the program. Then, each statement that has a symbolic variable is executed by symbolic manipulation. If a branch condition is found with a symbolic variable, then both paths are conceptually taken. The last step is using the path constraints to find the concrete values that allow the program to go down both paths. This is done until there are no more possible inputs. <ref name="chia" />
Scalar and Array Analysis
Scalar and Array Analysis are actually two different forms of analysis that are often used together. Scalar Analysis checks for dependencies between scalar variables in code. A dependency can be defined as "when a memory location written on one iteration of a loop is accessed (read or write) on a different iteration."<ref name="dipa" />
Array Analysis is then used on code that could not be parallelized using Scalar Analysis. Array Analysis looks for arrays that can be privatized.<ref name="dipa" /> Privatization means to allow each thread its own private copy of the array in question, in whole or in part. This is only possible if there are no dependencies in the array.<ref name="dipa" />
Commutativity Analysis
One problem in parallelizing code is that synchronization may be required in some programs to prevent errors in computation. Commutativity Analysis is used to determine which operations can be performed out of order without affecting the results of the code. It is based on the mathematical concept of commutativity, where if the result of running two operations is the same, regardless of which order they are performed in.<ref name="dipa" />
Low Level Virtual Machine
LLVM works by taking C/C++ code and compiling it into LLVM IR bytecode. Optimizations are done at the IR level and then a code generator brings it back into native code to be executed.<ref name="chia"/>
Limitations
One of the major limitations of automatic parallelization is that a computer lacks the insight into the overall intention of a program that a human would have. The programmer understands what the program must do, and can use that to determine if there are alternate approaches or algorithms for parallelizing the code. Even when parallelizing manually, a programmer may not have enough insight into parallel programming, and will need the assistance of an expert to improve code performance.<ref name="ncsa" />
References
<references> <ref name="chia">http://www.eecs.berkeley.edu/%7Echiayuan/cs262a/cs262a_parallel.pdf</ref> <ref name="dipa">http://www.csc.villanova.edu/%7Etway/publications/DiPasquale_Masplas05_Paper5.pdf</ref> <ref name="wiki">http://en.wikipedia.org/wiki/Automatic_parallelization</ref> <ref name="ncsa">http://www.ncsa.illinois.edu/extremeideas/site/on_the_limits_of_automatic_parallelization</ref> <ref name="polytope">http://en.wikipedia.org/wiki/Polytope_model</ref> </references>