CSC/ECE 506 Spring 2012/4b rs
The limits to speedup
Introduction <ref>http://en.wikipedia.org/wiki/Amdahl%27s_law</ref>
In parallel computing, speedup refers to how much a parallel algorithm is faster than a corresponding sequential algorithm. Parallel computing gains very high importance in scientific computations because of its good speedup. More so in those computations that involve large-scaled data. As far as the need for parallel computing goes, one claim is that we can always double the speed of a chip every 18 months according to Moore’s Law. This means there is no need to develop parallel computation. This claim however, has been proved to be wrong.
According to Amdahl's law the speedup of a program using multiple processors in parallel computing is limited by the time needed for the sequential fraction of the program. But this solves a fixed problem in the shortest possible period of time, rather than solving the largest possible problem (e.g., the most accurate possible approximation) in a fixed "reasonable" amount of time. To overcome these shortcomings, John L. Gustafson and his colleague Edwin H. Barsis described Gustafson's Law, which provides a counterpoint to Amdahl's law, which describes a limit on the speed-up that parallelization can provide, given a fixed data set size.
Scaled speedup
Scaled speedup is the speedup that can be achieved by increasing the data size. This increase in data size is done to solve a given problem on multiple parallel processors. In other words, with larger number of parallel processors at our disposal, we can increase the data size of the same problem and achieve higher speedup. This is what is referred to as scaled speedup. Means of achieving this speedup are exploited by Gustafson's Law.
Gustafson's Law <ref>http://en.wikipedia.org/wiki/Gustafson%27s_Law</ref>
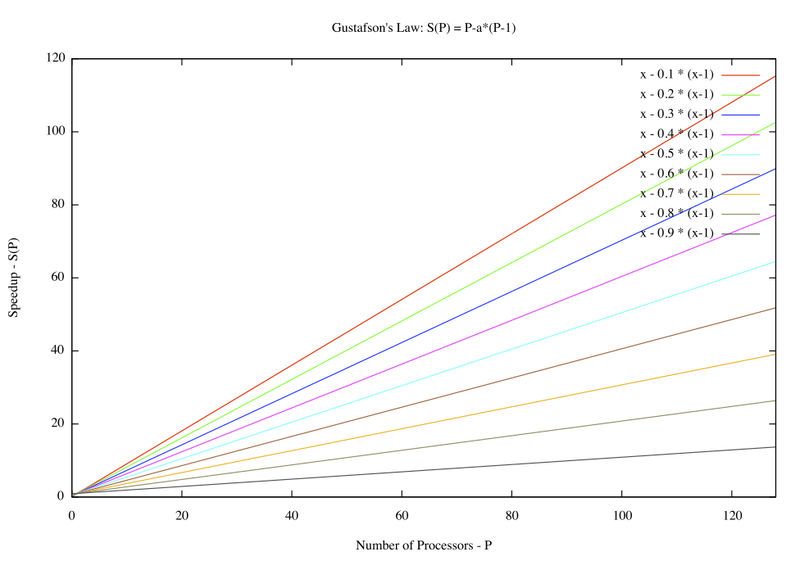
Gustafson's Law says that it is possible to parallelize computations when they involve significantly large data sets. It says that there is skepticism regarding the viability of massive parallelism. This skepticism is largely due to Amdahl's law, which says that the maximum speedup that can be achieved in a given problem with serial fraction of work s, is 1/s, even when the number of processors increases to an infinite number. For example, if 5% of computation in a problem is serial, then the maximum achievable speedup is 20 regardless of the number of processors. This is not a very encouraging result.
Amdahl's law does not fully exploit the computing power that becomes available as the number of machines increases. Gustafson's law addresses
this limitation. It considers the effect of increasing the problem size. Gustafson reasoned that when a problem is ported onto a multiprocessor system, it is possible to consider larger problem sizes. In other words, the same problem with a larger number of data values takes the same time. The law proposes that programmers tend to set the size of problems to use the available equipment to solve problems within a
practical fixed time. Larger problems can be solved in the same time if faster, i.e. more parallel equipment is available. Therfore, it should be possible to achieve high speedup if we scale the problem size.
Example:
s (serial fraction of work) = 5% p (number of processors) = 20 speedup (Amdahl's Law) = 10.26 scaled speedup (Gustafson's Law) = 19.05
Derivation of Gustafson's Law<ref>http://www.johngustafson.net/pubs/pub13/amdahl.pdf</ref><ref>http://en.wikipedia.org/wiki/Gustafson%27s_Law#Derivation_of_Gustafson.27s_Law</ref>
If p is the number of processors, s is the amount of time spent (by a serial processor) on serial parts of a program and 1-s is the amount of time spent (by a serial processor) on parts of the program that can be done in parallel, then Amdahl's law says that speedup is given by:
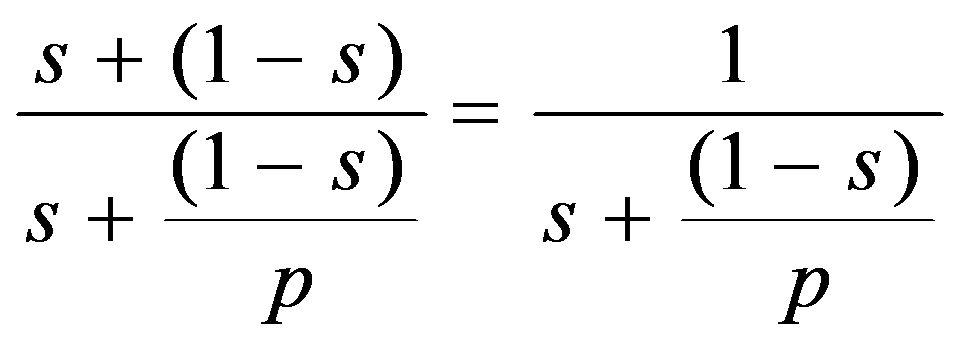
Let us consider a bigger problem size of measure n.
The execution of the program on a parallel computer is decomposed into:
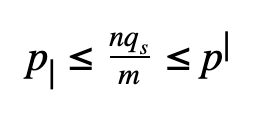
where a is the sequential fraction, 1-s is the parallel fraction, ignoring overhead for now, and p is the number of processors working in parallel during the parallel stage.
The relative time for sequential processing would be s + p (1 - s), where p is the number of processors in the parallel case.
Speedup is therefore:
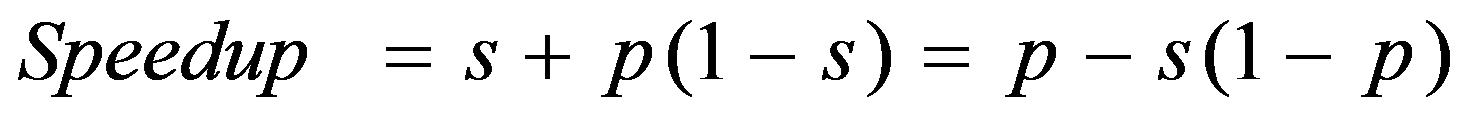
where s: = s(n) is the sequential fraction.
Assuming the sequential fraction s(n) diminishes with problem size n, then speedup approaches p as n approaches infinity, as desired. Thus Gustafson's law seems to rescue parallel processing from Amdahl's law.
Amdahl's law argues that even using massively parallel computer systems cannot influence the sequential part of a fixed workload. Since this part is irreducible, the sequential fraction of the fixed workload is a function of p that approaches 1 for large p. In comparison to that, Gustafson's law is based on the idea that the importance of the sequential part diminishes with a growing workload; and if n is allowed to grow along with p, the sequential fraction will not ultimately dominate.
In contrast with Amdahl's Law, this function is simply a line, and one with much more moderate slope: 1 – p.
It is thus much easier to achieve efficient parallel performance than is implied by Amdahl’s paradigm. The two approaches, fixed-sized and scaled-sized, are contrasted and summarized in Figure 2a and b.
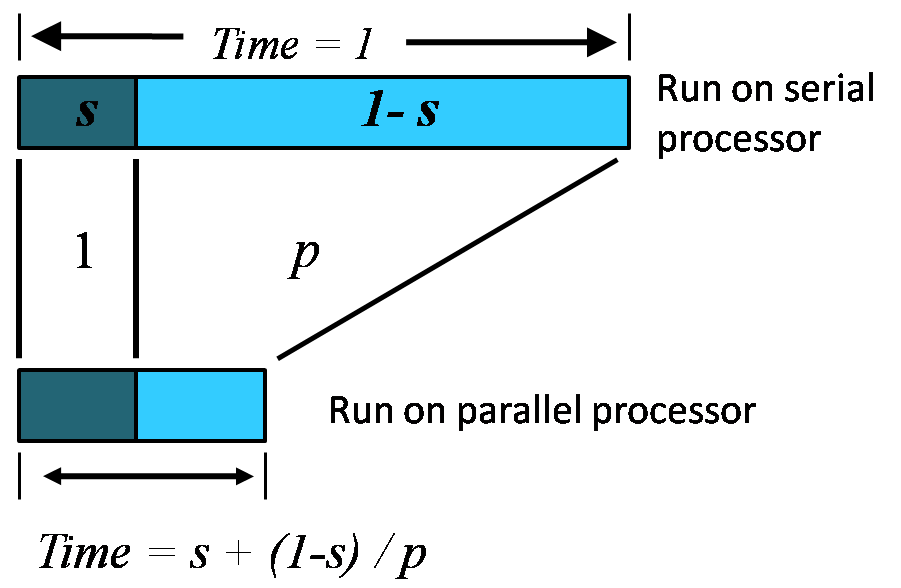

A Construction Metaphor
Amdahl's Law approximately suggests:
Suppose a 60 feet building is under construction, and 100 workers have spent 10 days to construct 30 feet at the rate of 3 feet / day. No matter how fast they construct the last 30 feet, it is impossible to achieve average rate of construction as 9 feet / day before completion of the building. Since they had already taken 10 days and there are only 60 feet in total; constructing infinitely fast you would only achieve a rate of 6 feet / day.
Gustafson's Law approximately states:
Suppose 100 workers are constructing a building at the rate of less than 9 feet / day. Given enough workers and height of building to construct, the average rate of construction can always eventually reach 9 feet / day, no matter how slow the construction had been. For example, 100 workers have spent 10 days to construct 30 feet at the rate of 3 feet / day, they could achieve this by more workers at the rate of 12 feet / day, for 20 additional days, or at the rate of 15 feet / day, for 10 additional days, and so on.
Gordon Bell prize <ref>http://techresearch.intel.com/ResearcherDetails.aspx?Id=182</ref> <ref>http://en.wikipedia.org/wiki/Gordon_Bell_Prize</ref>

The Gordon Bell Prizes are a set of awards awarded by the Association for Computing Machinery in conjunction with the Institute of Electrical and Electronics Engineers each year at the Supercomputing Conference to recognize outstanding achievement in high-performance computing applications. The main purpose of the award is to acknowledge, reward, and thereby assess the progress of parallel computing. The awards were established in 1987.
The Prizes were preceded by a similar much smaller prize (nominal: $100) by Alan Karp, a numerical analyst (then of IBM; won by Gustafson and Montry) challenging claims of MIMD performance improvements proposed in the Letters to the Editor section of the Communications of the ACM who went on to be one of the first Bell Prize judges. Cash prizes accompany these recognitions and are funded by the award founder, Gordon Bell, a pioneer in high-performance and parallel computing.
Dr. John L. Gustafson introduced the first commercial cluster system in 1985 and having first demonstrated 1000x, scalable parallel performance on real applications in 1988, for which he won the inaugural Gordon Bell Award. That demonstration broke the “Karp Challenge” that claimed speedup of more than 200x was a practical impossibility; it created a watershed that led to the widespread manufacture and use of highly parallel computers.
Superlinear speedup <ref>http://www.ccs.neu.edu/course/com3620/projects/scalable/jshan/final1.pdf</ref>
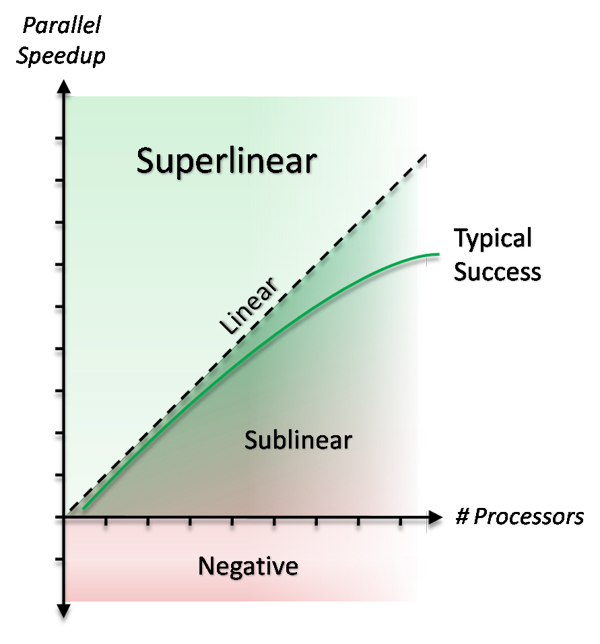
Not too long ago, the parallel time to solve a given problem using p processors was believed to be no greater than p. However, people then observed that in some computations the speedup was greater than p. When the speedup is higher than p, it is called super-linear speedup. One thing that could hinder the chances of achieving super-linear speedup is the cost involved in inter-process communication during parallel computation. This is not a concern in serial computation. However, super-linear speedup can be achieved by utilizing the resources very efficiently.
Controversy
Talk of super-linear speedup always sparks some controversy. Since super-linear speedup is not possible in theory, some non-orthodox practices could be thought of being the cause for achieving super-linear speedup. This is true especially with regard to the traditional research community. Hence, reporting super-linear speedup is controversial.
Reasons for super-linear speedup
Let us look at the reasons for super-linear speedup. The data set of a given problem could be much larger than the cache size when the problem is executed serially. In parallel computation, however, the data set has enough space in each cache that is available. In problems that involve searching a data structure, multiple searches can be executed at the same time. This reduces the termination time. Another reason is the efficient utilization of resources by multiprocessors.
Reasons for the discrepancy in the 'Parallel Search' <ref>http://stackoverflow.com/questions/4332967/where-does-super-linear-speedup-come-from</ref>
When search is being performed in parallel on multiple processors, the amount of work being done is lesser than the amount of work being done serially. Let us see why this is so:
- The parallel algorithm uses some search like a random walk, the more processors that are walking, the less distance has to be walked in total before you reach what you are looking for.
- Modern processors have faster and slower memories. The processor will try to keep the data we are using in the fast memory. The amount of our data is most likely larger than the amount of fast memory. If we use n processors we have n times the amount of faster memory. More data fits in the fast memory which makes it possible to take less time, and hence amount of work to do the same task.
- The original sequential algorithm was really bad
- There are multiple processors at our disposal and hence much more cache is available when compared to serial computation on a single processor. The serial algorithm always runs out of cache space when the data set is very large.
- Getting a serial algorithm to do this parallel work and get better results wouldn't be feasible because the serial algorithm will not utilize the resources efficiently like a parallel algorithm would.
Super-linearity on a large machine <ref>http://drdobbs.com/article/print?articleId=206903306&siteSectionName=</ref>
So far we have looked at leveraging the super-linearity that can arise naturally in parallel computation. Now let us think how else we could achieve super-linear speedup. We could use more parallelism on the same machine. To speed up computational work we can increase the number of cores that we use. However, using more cores will only give us linear speedup.
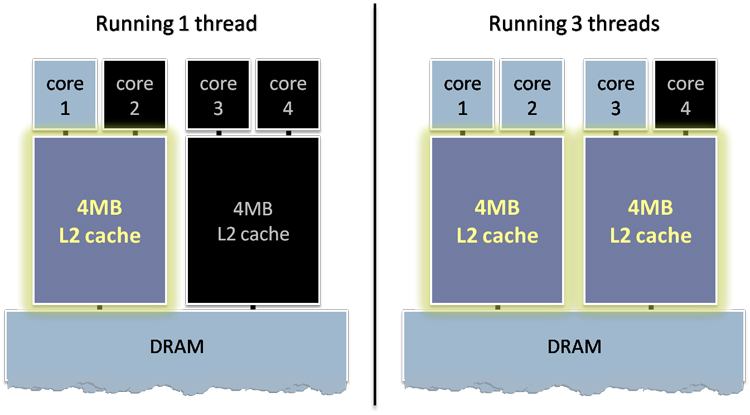
When you run a program with less parallelism and another with more parallelism on the same modern desktop or server hardware, the one with more parallelism literally runs on a bigger machine — a disproportionately larger share of the available hardware. This happens because the one with more parallelism can use not only additional cores, but additional hardware resources attached to those cores that would not otherwise be available to the program. In particular, using more cores also means getting access to more cache and/or more memory.
Let us take a look at Figure 4 to see why this is so. This figure shows a simplified block diagram of the cores and caches on two modern commodity CPUs: the current Intel "Kentsfield" processor, and the upcoming AMD "Barcelona" processor, respectively. The interesting feature in both chips is that each core has access to cache memory that is not available to some or all of the other cores. In the Kentsfield processor, each pair of cores shares a private L2 cache; in the Barcelona chip, each core has its own private L2 cache. In both cases, no core by itself has access to all the available L2 cache, and that means that code running on just one core is limited, not only to the one core, but also to just a fraction of the available cache. For code whose performance is memory bound, the amount of available cache can make a significant difference.
Example:
Suppose we have an 8 processor machine, each processor has a 1MB cache and each computation uses 6MB of data. On a single processor the computation will be doing a lot of data movement between CPU, cache and RAM. On 8 processors the computation will only have to move data between CPU and cache. This way super-linear speedup can be achieved.
Conclusion
Scaled speedup <ref>http://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&sqi=2&ved=0CCkQFjAB&url=http%3A%2F%2Fcoitweb.uncc.edu%2F~abw%2FITCS4145F10%2Fslides1a.ppt&ei=rq05T_zOOpKutwe635jRAg&usg=AFQjCNFMNTKEQ2P9G4zV3fGWyaMbmYtsMQ</ref><ref>http://spartan.cis.temple.edu/shi/public_html/docs/amdahl/amdahl.html</ref>
Using Amdahl's Law as an argument against massively parallel processing is not valid. This is because serial parts of a program can be very close to zero for many practical applications. Thus very high speedups are possible using massively many processors. Gustafson's experiments are just examples of these applications.
Gustafson's formulation gives an illusion that as if number of processors can increase indefinitely. A closer look finds that the increase in serial parts of a program is affecting speedup negatively. The rate of speedup decrease as number of processors approaches infinity, if we translate the scaled-percentage to a non-scaled percentage. We cannot observe the speedup impact by number of processors using Gustafson's formulation directly since it contains a number of processors dependent variable serial parts of a program.
Even though Amdahl's law is theoretically correct, the serial percentage is not practically obtainable. For example, if the serial percentage is to be derived from computational experiments, i.e. recording the total parallel elapsed time and the parallel-only elapsed time, then it can contain all overheads, such as communication, synchronization, input/output and memory access. The law offers no help to separate these factors. On the other hand, if we obtain the serial percentage by counting the number of total serial and parallel instructions in a program, then all other overheads are excluded. However, in this case the predicted speedup may never agree with the experiments.
Conclusion drawn from Gustafson’s law is that it should be possible to get high speedup if we scale up the problem size.
Super-linear speedup
Even though in theory the maximum possible speedup is equal to the number of parallel processors, in practice we do see speedups higher than the number of processors, or in other words, super-linear speedup. It is considered controversial by purists because of the skepticism regarding the means of achieving this high speedup. If super-linear speedup is achievable, it gives an extremely high degree of parallelism and also provides maximum utilization of resources.
External links
2. Figure 1 - Plot of speedup vs processors - Gustafson's Law
3. Figure 3 - Superlinear speedup
5. Controversy
6. Figure 4 - Intel Kentsfield core and cache utilization: 1 thread versus 3 threads.
8. Intel "Kentsfield" processor
References
<references/>