CSC/ECE 506 Spring 2012/3a df
Patterns of Parallel Programming
Introduction
Computer programming has gone through several paradigm shifts in regards to how software is design and constructed. In more recent years with the advent of object-oriented programming, an effort was made by the "Gang of Four" to categorize different arrangements and relationships between programming objects in terms of commonly used design patterns. In a similar vein, with recent advances in parallel programming and availability of hardware, there are several common designs that can be drawn from the vast amount of literature available. Although there exists no canonical text for parallel programing as there exists for object oriented programming, there is substantial overlap, which is presented here.
Overall, programming patterns can be split into three categories of similar abstraction: intuitive, common, and complex, with each having involvement with architecture, design, and idioms.<ref name="ortega">Ortega-Arjona, Jorge Luis. Patterns for Parallel Software Design. Hoboken, NJ: John Wiley, 2010</ref> An architectural pattern defines software organization, a design pattern is a refinement of an architectural pattern in regards to solving a particular pattern, and an idiom is a particular implementation of a design pattern in a programming language or framework. This chapter will focus on architectural and design patterns.
Intuitive Patterns
Intuitive patterns are termed as such because even those with basic knowledge of parallel processes could create their design. They are obvious, straight-forward applications of parallel computing tasks, and their implementation and use are easily implemented even without specialized software packages or advanced algorithm development.
"Embarrassingly" Parallel
Embarrassingly parallel patterns<ref name="kim_ppp_ppt">Parallel Programming Patterns by Eun-Gyu Kim</ref> are those in which the tasks to be performed are completely disparate. Specifically, these operations occur when the datasets of concern are able to be abstracted to a point where the resources are not in contention. Examples abound of this behavior in productivity programs like Microsoft Word or Outlook, when a spell-check or auto-archive operation is in progress.
Replicable
Description
The Replicable pattern comes from the fact that data available to all processes needs to be duplicated for use in other processes<ref name="kim_ppp_ppt"/>. This necessitates a reduction step where the results from all of the tasks is analyzed for the total final result. An application of this pattern could be in certain kinds of encryption algorithms where a set of data can be broken into "chunks" of a particular size, decrypted seperately, and joined back together at the end.
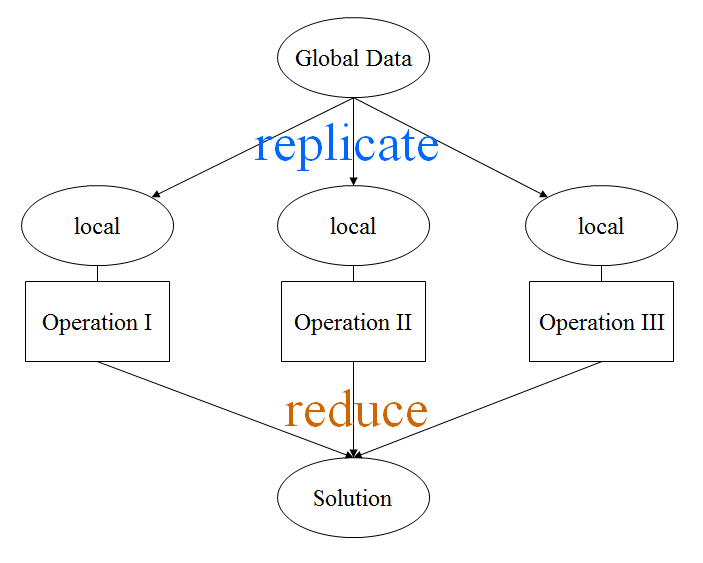
Example
Because the Replicable pattern is so important to subsequent patterns, a fully developed example using C and OpenMP (mentioned later in this chapter) is provided below.
Code Listing
// This code example for the Replicable pattern spawns four threads which copy
// the data and proceed to reverse it and place it back into a global results
// array. Tested in Microsoft Visual Studio 2010 with /openmp and /TC compile options
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
#include <omp.h>
#define CHUNK_SIZE 4
void OutputData(char *pArray, int size);
int main()
{
int i, j;
char temp;
char *localData;
const char globalData[] =
{ 3, 2, 1, 0,
7, 6, 5, 4,
11, 10, 9, 8,
15, 14, 13, 12 };
char globalResult[CHUNK_SIZE*CHUNK_SIZE];
// Setup and report
omp_set_nested(1);
omp_set_num_threads(4);
printf("Data set: "); OutputData(globalData, CHUNK_SIZE*CHUNK_SIZE); printf("\n");
printf("Running Replicable parallel section...\n");
#pragma omp parallel for private(i,j,localData) schedule(static)
for(i = 0; i < CHUNK_SIZE; i++)
{
// Replicate data for local use
localData = (char *)malloc(sizeof(char)*CHUNK_SIZE);
memcpy(localData, (char *)(globalData+i*CHUNK_SIZE), sizeof(char)*CHUNK_SIZE);
// Reverse the chunk
for(j = 0; j < CHUNK_SIZE/2; j++)
{
temp = localData[CHUNK_SIZE - j - 1];
localData[CHUNK_SIZE - j - 1] = localData[j];
localData[j] = temp;
}
// Merge the results back into the global result and clean up
memcpy((char *)(globalResult+i*CHUNK_SIZE), localData, sizeof(char)*CHUNK_SIZE);
free(localData);
printf("-> Merged result in thread %d/%d\n", omp_get_thread_num()+1, omp_get_num_threads());
}
// Output the results of the parallel section
printf("Results: "); OutputData(globalResult, CHUNK_SIZE*CHUNK_SIZE); printf("\n");
system("pause");
return 0;
}
// Convenience method for reporting the results
void OutputData(const char *pArray, int size)
{
int i;
for(i = 0; i < size; i++) printf("%d,", pArray[i]);
printf("\b ");
}
Results
Execution of this compiled program in the Microsoft Windows 7 operating system yielded the following output. Notice how the threads actually executed out of order, and that the final output is still correct as the ordered list of numbers.
Data set: 3,2,1,0,7,6,5,4,11,10,9,8,15,14,13,12 Running Replicable parallel section... -> Merged result in thread 1/4 -> Merged result in thread 2/4 -> Merged result in thread 4/4 -> Merged result in thread 3/4 Results: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 Press any key to continue . . .
Repository
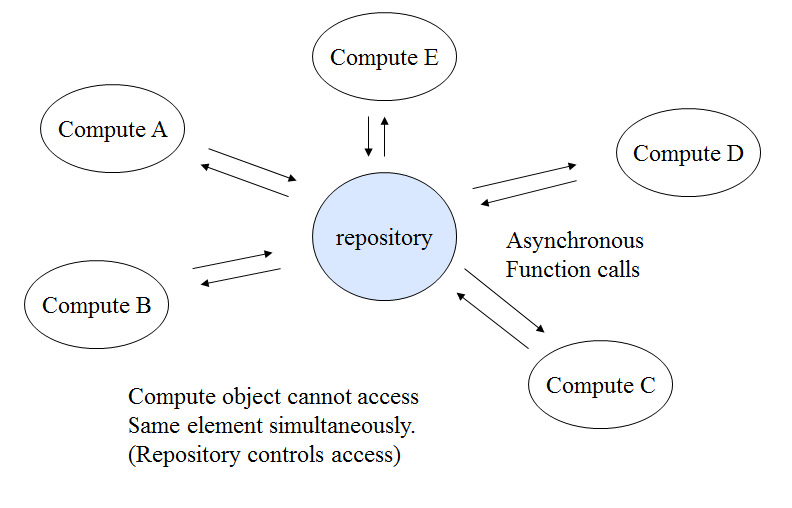
The Repository pattern is related to the Replicable pattern in that they both act on a set of data and rely on the result<ref name="kim_ppp_ppt"/>. However, in the Repository pattern all data remains centralized while the computations themselves are performed remotely. In essence, the Repository pattern could be thought of as a continuous Replicable pattern where the global data set is much larger than can be simultaneously replicated. An excellent (simplified) example of this pattern would be distributed computing applications like Folding@Home or SETI@Home, where a central server coordinates the calculations between all available processing units.
Divide and Conquer
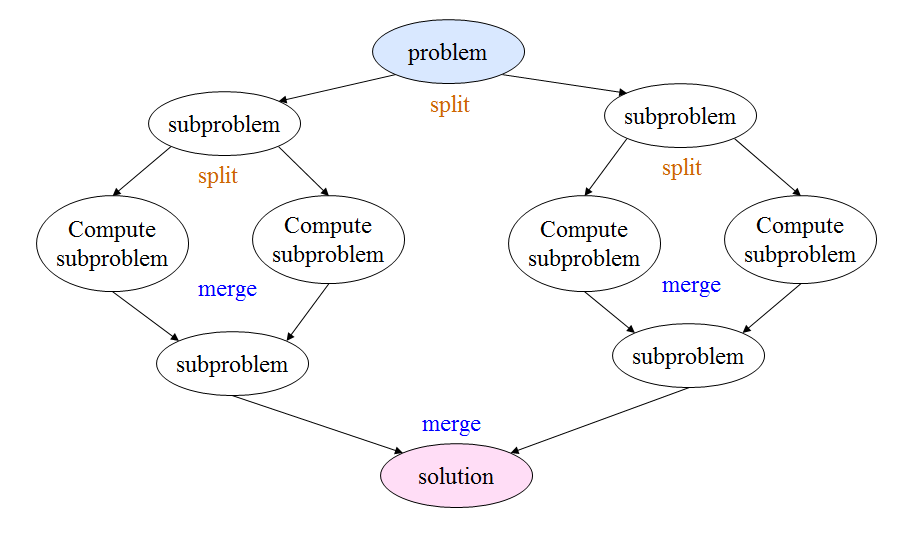
The Divide and Conquer pattern is very similar to the Replicable pattern<ref name="kim_ppp_ppt"/>. It involves taking a problem or task and splitting it into subproblems whereupon the required calculations are performed in parallel. A merging action still needs to occur to arrive at the solution, but the advantage of Divide and Conquer over Replicable is that the entire data set does not have to be communicated between the processing units -- only the required data for the computation does. Also, due to the degree of separation of computation and data, there is a non-negligible amount of overhead associated with determining the proper points at which the problems should be split and the overall allocation of resources.
Common Patterns
Common patterns solve parallel design tasks that are readily understood and frequently encountered, but whose implementation could benefit from a more formalized and structured approach. Generally, common parallel patterns can be implemented manually or with a framework with a moderate degree of difficulty depending on the programmer's skill level.
Pipeline
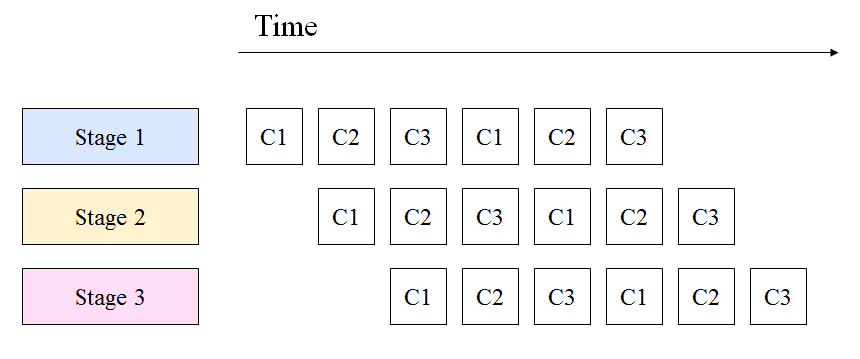
The Pipeline pattern<ref name="kim_ppp_ppt"/> is a hybrid of the “Embarrassingly” Parallel pattern as well as the Replicable pattern. The best way to think of the Pipeline pattern is as an assembly line <ref name=”pipeline_wiki”>Pipeline (computing) on Wikipedia</ref>. Suppose there are three steps in assembling a computer: un-packaging the internals, installing the internals, and performing a first-boot diagnostic, all of which take 15 minutes each. In a serial pattern, the entire process takes 45 minutes for one assembled computer, and it takes 45 more minutes for another computer to be assembled. In a Pipeline pattern, however, that same process would still have the same latency (since it takes 45 minutes for a particular computer to be built), but the overall throughput is increased because a computer in general is completed every 15 minutes after the first one.
Pipelining differs from the Replicable pattern because in Pipeline only one copy of the resources is available. Referring back to the assembly line example, there is only one station for un-packaging, one station for installation, and one station for diagnostics. In a Replicable pattern, however, each work stream would have its own copy of the resources, so that the same steps could occur simultaneously. To be sure, this does nothing for latency, but has the capability to increase throughput dramatically.
Recursive Data
The Recursive Data pattern<ref name="kim_ppp_ppt"/> presents an interesting problem for parallel algorithms; while the need is common, its solution can be very complex depending on the data structure. In general, when working with recursive data structures, it is desired for any and all commonalities and reductions to be established in order to minimize the operations required to traverse the structure. Once the structure is mapped (or its behavior analyzed), other parallel patterns can be employed. One possible example is that of an electric utility’s mesh network of smart meters. Hub (head-end) units where data is aggregated need to employ parallel processing in order to efficiently collect usage data. For smaller hubs, it might be beneficial to communicate directly with the meters, whereas for larger hubs it may be more prudent to communicate with smaller hubs. In such a case, Recursive Data can be paired with Divide & Conquer to come to a solution much faster than its serial or naively parallel alternatives.
Geometric

The Geometric pattern<ref name="kim_ppp_ppt"/> is a specialized implementation of the Divide & Conquer pattern. It differs in that there is sharing of data on boundaries of the problem, be that the first and last elements of different sets (1D), perimeters (2D), or faces (3D). The significant difference between the Geometric and Divide & Conquer patterns is that in the Geometric pattern, there is ideally no sub-problem step, as the inter-process communication that might occur is used in the current process’ calculation and does not have to subsequently be calculated. A great example of the Geometric pattern is a fluid simulation, where a matrix (or higher dimension such as cubic or quartic) data set must be analyzed for changes in motion.
Irregular Mesh

The Irregular Mesh pattern<ref name="kim_ppp_ppt"/> is a hybrid of the Geometric and Recursive Data patterns (and sub-patterns implied); Geometric because of the boundaries involved with splitting up the shape, and Recursive Data due to the varying hierarchies that might be involved. An example of this kind of operation would be a skeletal/bone structure system for three-dimensional computer models. A difficult task for even serial computation, the Irregular Mesh pattern is difficult to implement in an optimal manner without careful consideration to the algorithm and having insight as to what kind of structure is being analyzed.
Inseparable
The Inseparable pattern<ref name="kim_ppp_ppt"/> is more of an anti-pattern in that it is a problem which needs a parallel solution, but whose solution does not seem to fit any of the aforementioned patterns. Frequently, but not always, the Inseparable pattern will utilize the parallel primitives in complex and non-deterministic ways, and may actually be representative of programming errors or a lack of organization. There does not always have to be a negative connotation, however, as a problem may be so complex as to not fit into any of the above patterns.
Complex Patterns
Complex patterns involve the interplay between two or more parallel patterns, or are a single pattern that greatly deviates from a common implementation itself. Such algorithms require moderate to advanced programmer skill, and are almost always accompanied by a framework or involve a significant amount of custom "infrastructural" code to accomodate the needs of the architecture.
- Multi-grid<ref>Multigrid Pattern at UIUC Computer Science Department</ref> - Multiple geometric grids are employed with an iterative solver in order to determine efficient grid granularity
- Multi-domain<ref>Multi-domain Pattern at UIUC Computer Science Department</ref> - Leverage different mathematical domains (spatial, frequency; Fourier, Laplace) to come to a solution more quickly
- Odd-Even Communication Group<ref>Odd-Even Communication Group at UIUC Computer Science Department</ref> - Recursive data structure that allows for more efficient operations on nodes
- Loosely Synchronous<ref>Loosely Synchronous Model As Parallel Structure at UIUC Computer Science Department</ref> - Use of phases to simplify the assumptions on parallel processes
- Event Driven<ref>Event-Driven Pattern at UIUC Computer Science Department</ref> - Allow implicated processes to alert each other to re-commence calculation
Formalization
Formalization describes the efforts of the programming community to devise tools which can aid programmers in designing software which follows standardized (whether international/documented or by practice) procedures, methods, and templates for performing parallel operations. These tools may be purely documentation pieces, frameworks, examples, academic papers, etc.
Design Languages
Design languages allow programmers to define problems in terms of a common vocabulary so that solutions to problems can be readily identified and efficiently shared.<ref name="ortega"/> A brief survey of some current pattern language efforts follows.
ParLab
The Pattern Language for Parallel Programming at Berkeley’s ParLab<ref name=”parlab”>[ http://parlab.eecs.berkeley.edu/wiki/patterns/patterns A Pattern Language for Parallel Programming] at Berkely ParLab</ref> describes five major categories of patterns. These patterns are described through a somewhat disparate documentation set and articles:
- Structural Patterns - Concerned with the arrangement of different processes that can run in parallel
- Computation Patterns - Concerned with the way parallel processes handle data
- Parallel Algorithm Strategy Patterns - Descriptions on how different end results can be achieved by using parallel algorithms
- Implementation Strategy Patterns - Descriptions on the mechanisms that can be used to implement parallel algorithms
- Concurrent Execution Patterns - Concerned with how parallel processes should be managed
University of Florida PLPP
The development efforts of a pattern language for parallel patterns undertaken at the University of Florida resulted in the development of a published text<ref name=”ufl”>Mattson, Timothy G., Beverly A. Sanders, and Berna Massingill. Patterns for Parallel Programming. Boston: Addison-Wesley, 2005. Homepage</ref>. This book catalogs the major “design spaces,” or “solution to a problem in context,” which are<ref name=”ufl_toc”>Mattson, Timothy G., Beverly A. Sanders, and Berna Massingill. Patterns for Parallel Programming. Boston: Addison-Wesley, 2005. Table of Contents</ref>:
- Finding Concurrency - How a problem can be parallelized in the first place
- Algorithm Structure - How the processes can be arranged (see Intuitive and Common patterns earlier in this chapter)
- Supporting Structures - Primitives and data structures useful in managing parallel tasks
- Implementation Mechanisms - Architecture and resource-specific details on creating parallel solutions
Frameworks
Frameworks are any piece of code for a particular programming language which can help a programmer in creating a program which takes advantage of parallel algorithms. A discussion of the frameworks is outside the scope of this chapter, but the interested reader is suggested to investigate the following resources:
- Parallel Patterns Library - Programming library for parallel processes in Microsoft's .NET Framework
- OpenMP - Application programminf interface for parallel processes in the C/C++ and Fortran programming languages
- SWARM - Application programming interface based on POSIX Threads that implements several parallel primitives
Summary
In conclusion, there are currently many initiatives to standardize the programmer’s experience when designing and maintaining parallel software systems. Through the survey above, it can be noted that there are four key factors in determining which parallel pattern to use:
- Physical resources available - The amount of processing units, memory, communication bandwidth, etc.
- Algorithm data parallelism - How well the algorithm’s data can be split up to be used in independent calculations
- Algorithm computation parallelism - How much each processor must rely on another for its intermediate calculations
- Framework/programming language - What limiting factors might exist for implementing the desired pattern in the programming language or framework of choice.
Indeed, there is a pattern for nearly every occasion, and the patterns presented above are just the "key" patterns. However, without careful consideration of the above points, the programmer will find difficulty in optimally implementing his or her software.
See Also
- Resources on Parallel Patterns at the UIUC Computer Science Department
References
<references></references>