CSC/ECE 506 Spring 2011/ch2 cl

From Expertiza_Wiki
Jump to navigation Jump to search

Supplement to Chapter 2: The Data Parallel Programming Model

Chapter 2 of Solihin (2008) covers the shared memory and message passing parallel programming models. However, it does not address the data parallel model, another commonly recognized parallel programming model covered in other treatments like Foster (1995) and Culler (1999). Whereas the shared memory and message passing models are often present as competing models, the data parallel model addresses fundamentally different programming concerns and can therefore be used in conjunction with either. The goal of this supplement is to provide a treatment of the data parallel model which complements Chapter 2 of Solihin (2008). The task parallel model will also be introduced as a point of contrast.

Overview

Whereas the shared memory and message passing models focus on how parallel tasks access common data, the data parallel model focuses on how to divide up work into parallel tasks. Data parallel algorithms exploit parallelism by dividing a problem into a number of identical tasks which execute on different subsets of common data. Hillis (1986) points out that a major benefit of data parallel algorithms is that they easily scale to take advantage of additional processing elements simply by dividing the data into smaller chunks. Haveraaen (2000) also notes that data parallel codes typically bear a strong resemblance to sequential codes, making them easier to read and write.

Example of Data Parallel Programing Model

This section shows a simple example adapted from Solihin textbook (pp. 24 - 27) that illustrates the data-parallel programming model. Each of the codes below are written in pseudo-code style.


Suppose we want to perform the following task on an array a: updating each element of a by the product of itself and its index, and adding together the elements of a into the variable sum. The corresponding code is shown below. 


// simple sequential task
sum = 0;
for (i = 0; i < a.length; i++)
{
   a[i] = a[i] * i;
   sum = sum + a[i];
}


When we orchestrate the task using the data-parallel programming model, the program can be divided into two parts. The first part performs the same operations on separate elements of the array for each processing element (sometimes referred to as PE or pe), and the second part reorganizes data among all processing elements (In our example data reorganization is summing up values across different processing elements). Since data-parallel programming model only defines the overall effects of parallel steps, the second part can be accomplished either through shared memory or message passing. The three code fragments below are examples for the first part of the program, shared-memory version of the second part, and message passing for the second part, respectively. 


// data parallel programming: let each PE perform the same task on different pieces of distributed data
pe_id = getid();
my_sum = 0;
for_all (i = pe_id; i < a.length; i += number_of_pe)         //separate elements of the array are assigned to each PE 
{
   a[i] = a[i] * i;
   my_sum = my_sum + a[i];                               //all PEs accumulate elements assigned to them into local variable my_sum
}


In the above code, data parallelism is achieved by letting each processing element perform actions on array's separate elements, which are identified using the PE's id. For instance, if three processing elements are used then one processing element would start at i = 0, one would start at i = 1, and the last would start at i = 2. Since there are three processing elements then the index of the array for each will increase by three on each iteration until the task is complete (note that in our example elements assigned to each PE are interleaved instead of continuous). If the length of the array is a multiple of three then each processing element takes the same amount of time to execute its portion of the task.


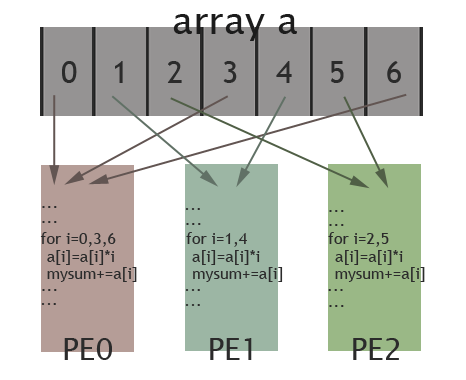
The picture below illustrates how elements of the array are assigned among different PEs for the specific case: length of the array is 7 and there are 3 PEs available. Elements in the array are marked by their indexes (0 to 6). As shown in the picture, PE0 will work on elements with index 0, 3, 6; PE1 is in charge of elements with index 1, 4; and elements with index 2, 5 are assigned to PE2. In this way, these 3 PEs work collectively on the array, while each PE works on different elements. Thus, data parallelism is achieved.

Illustration of data parallel programming(adapted from Introduction to Parallel Computing)

Task Parallel Overview

The logical opposite of data parallel is task parallel, in which a number of distinct tasks operate on common data.

Example of Task Parallel Programming Model

An example of a task parallel code which is functionally equivalent to the sequential and data parallel codes given above follows below. 

// Task parallel code.

int id = getmyid(); // assume id = 0 for thread 0, id = 1 for thread 1

if (id == 0)
{
    for (i = 0; i < 8; i++)
    {
        a[i] = b[i] + c[i];
        send_msg(P1, a[i]);
    }
}
else
{
    sum = 0;
    for (i = 0; i < 8; i++)
    {
        recv_msg(P0, a[i]);
        if (a[i] > 0)
            sum = sum + a[i];
    }
    Print sum;
}

In the code above, work is divided into two parallel tasks. The first performs the element-wise addition of arrays b and c and stores the result in a. The other sums the elements of a. These tasks both operate on all elements of a (rather than on separate chunks), and the code executed by each thread is different (rather than identical).

Since each parallel task is unique, a major limitation of task parallel algorithms is that the maximum degree of parallelism attainable is limited to the number of tasks that have been formulated. This is in contrast to data parallel algorithms, which can be scaled easily to take advantage of an arbitrary number of processing elements. In addition, unique tasks are likely to have significantly different run times, making it more challenging to balance load across processors. Haveraaen (2000) also notes that task parallel algorithms are inherently more complex, requiring a greater degree of communication and synchronization. In the task parallel code above, after thread 0 computes an element of a it must send it to thread 1. To support this, sends and receives occur every iteration of the two loops, resulting in a total of 8 messages being sent between the threads. In contrast, the data parallel code sends only 2 messages, one at the beginning and one at the end.


Comparison between Data and Task Parallel Programming Models

Comparison between data parallel and task parallel programming models.
Aspects Data Parallel Task Parallel
Decomposition Partition data into subsets Partition program into subtasks
Parallel tasks Identical Unique
Degree of parallelism Scales easily Fixed
Load balancing Easier Harder
Communication overhead Lower Higher

Synchronous vs Asynchronous

While the lockstep imposed by data parallelism on all data streams ensures synchronous computation (all PEs perform their tasks at the exact same pace), every processor in task parallelism performs its task at their own pace, which we call asynchronous computation. Thus, at a certain point of a task parallel program's execution, communication and synchronization primitives are needed to allow different instruction streams to coordinate their efforts, and that is where variable-sharing and message-passing come into play.

Determinism vs. Non-Determinism

Data parallelism's synchronous nature and task parallelism's asynchronism give rise to another pair of features that add to the difference between these two models: determinism versus non-determinism. Data parallelism is deterministic, i.e. computing with the same input will always yield the same result, since its synchronism ensures that issues like relative timing between PEs will not arise. In contrast, task parallelism's asynchronous updates of common data can give rise to non-determinism, i.e, the same input won't always yield the same computation result (the result of a computation will depend also on factors outside the program control, such as scheduling and timing of other PEs). Obviously, non-determinism makes it harder to write and maintain correct programs. This partially explains the advantage of data parallel programming model over data parallelism in terms of development effort (also discussed in section 4.2).

Comparison Diagram

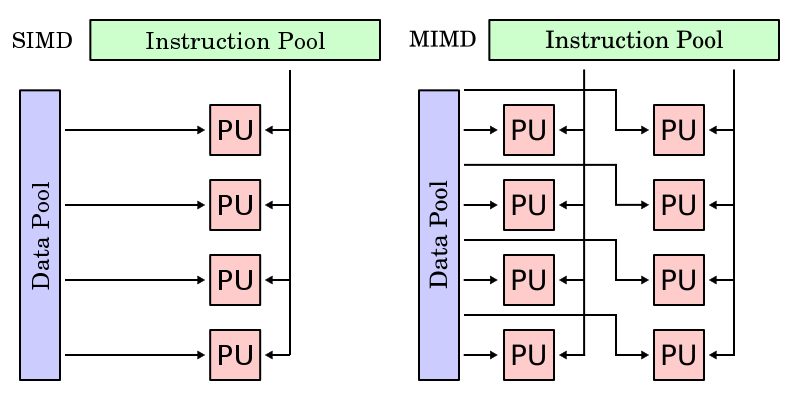
The following diagram may be of use conceptually distinguishing between data parallelism (SIMD: Single Instruction, Multiple Data) and task parallelism (MIMD: Multiple Instruction, Multiple Data). In the SIMD, it is observed that a single instruction runs to multiple processors which then access multiple connections to the data. In contrast, the MIMD has multiple instruction streams (evidenced by two groups of processors) which interact, again, with multiple connections to the data

contrast between data parallelism and task parallelism (PU (Processing Unit) and PE (processing Element) are synonymous

History of Parallel Programming Models

Interesting Dates in Parallel Computing History (with a focus on IBM, Cray, and ILLIAC)

1950's

  • 1955
    • IBM introduces the 704. Principal architect is Gene Amdahl; it is the first commercial machine with floating-point hardware, and is capable of approximately 5 kFLOPS.
  • 1956
    • IBM starts 7030 project (known as STRETCH) to produce supercomputer for Los Alamos National Laboratory (LANL). Its goal is to produce a machine with 100 times the performance of any available at the time.
  • 1958
    • Bull of France announces the Gamma 60 with multiple functional units and fork & join operations in its instruction set. 19 are later built.
    • John Cocke and Daniel Slotnick discuss use of parallelism in numerical calculations in an IBM research memo. Slotnick later proposes SOLOMON, a SIMD machine with 1024 1-bit PEs, each with memory for 128 32-bit values. The machine is never built, but the design is the starting point for much later work.

1960's

  • 1960
    • Atlas computer becomes operational. It is the first machine to use virtual memory and paging; its instruction execution is pipelined, and it contains separate fixed- and floating-point arithmetic units, capable of approximately 200 kFLOPS.
    • Burroughs introduces the D825 symmetrical MIMD multiprocessor. 1 to 4 CPUs access 1 to 16 memory modules using a crossbar switch. The CPUs are similar to the later B5000; the operating system is symmetrical, with a shared ready queue.
  • 1964
    • Daniel Slotnick proposes building a massively-parallel machine for the Lawrence Livermore National Laboratory (LLNL); the Atomic Energy Commission gives the contract to CDC instead, who build the STAR-100 to fulfil it. Slotnick's design funded by the Air Force, and evolves into the ILLIAC-IV. The machine is built at the University of Illinois, with Burroughs and Texas Instruments as primary subcontractors. Texas Instruments' Advanced Scientific Computer (ASC) also grows out of this initiative.
  • 1966
    • Michael Flynn publishes a paper describing the architectural taxonomy which bears his name.
  • 1967
    • IBM produces the 360/91 (later model 95) with dynamic instruction reordering. 20 of these are produced over the next several years; the line is eventually supplanted by the slower Model
    • Gene Amdahl and Daniel Slotnick have published debate at AFIPS Conference about the feasibility of parallel processing. Amdahl's argument about limits to parallelism becomes known as "Amdahl's Law"; he also propounds a corollary about system balance (sometimes called "Amdahl's Other Law"), which states that a balanced machine has the same number of MIPS, Mbytes, and Mbit/s of I/O bandwidth.
  • 1968
    • IBM 2938 Array Processor delivered to Western Geophysical (who promptly paint racing stripes on it). First commercial machine to sustain 10 MFLOPS on 32-bit floating-point operations. A programmable digital signal processor, it proves very popular in the petroleum industry.
    • Edsger Dijkstra describes semaphores, and introduces the dining philosophers problem, which later becomes a standard example in concurrency theory.
  • 1969
    • George Paul, M. Wayne Wilson, and Charles Cree begin work at IBM on VECTRAN, an extension to FORTRAN 66 with array-valued operators, functions, and I/O facilities.
    • Work begins at Compass Inc. on a parallelizing FORTRAN compiler for the ILLIAC-IV called IVTRAN.

1970's

  • 1971
    • Intel produces the world's first single-chip CPU, the 4004 microprocessor.
  • 1972
    • Seymour Cray leaves Control Data Corporation to found Cray Research Inc. CDC cancels the 8600 project, a follow-on to the 7600.
    • Quarter-sized (64 PEs) ILLIAC-IV installed at NASA Ames. Each processor has a peak speed of 4 MFLOPS; the machine's I/O system is capable of 500 Mbit/s.
    • Paper studies of massive bit-level parallelism done by Stewart Reddaway at ICL. These later lead to development of ICL DAP.
  • 1974
    • Leslie Lamport's paper "Parallel Execution of Do-Loops" lays the theoretical foundation for most later research on automatic vectorization and shared-memory parallelization. Much of the work was done in 1971-2 while Lamport was at Compass Inc.
    • IBM delivers the first 3838 array processor, a general-purpose digital signal processor.
  • 1975
    • ILLIAC-IV becomes operational at NASA Ames after concerted check-out effort.
  • 1976
    • Cray Research delivers the first Freon-cooled CRAY-1 to Los Alamos National Laboratory.
  • 1979
    • IBM's John Cocke designs the 801, the first of what are later called RISC architectures.

1980's

  • 1980
    • PFC (Parallel FORTRAN Compiler) developed at Rice University under the direction of Ken Kennedy.
    • David Padua and David Kuck at the University of Illinois develop the DOACROSS parallel construct to be used as a target in program transformation. The name DOACROSS is due to Robert Kuhn.
  • 1982
    • Steve Chen's group at Cray Research produces the first X-MP, containing two pipelined processors compatible with the CRAY-1 and shared memory.
    • ILLIAC-IV decommissioned.
  • 1983
    • J. R. Allen's Ph.D. thesis at Rice University introduces the concepts of loop-carried and loop-independent dependencies, and formalizes the process of vectorization.
    • Scientific Computer Systems founded to design and market Cray-compatible minisupercomputers.
    • CRAY-1 with 1 processor achieves 12.5 MFLOPS on the 100x100 LINPACK benchmark.
  • 1984
    • The CRAY X-MP family is expanded to include 1- and 4-processor machines. A CRAY X-MP running CX-OS, the first Unix-like operating system for supercomputers, is delivered to NASA Ames.
    • CRAY X-MP with 1 processor achieves 21 MFLOPS on 100x100 LINPACK.
  • 1985
    • Cray Research produces the CRAY-2, with four background processors, a single foreground processor, a 4.1 nsec clock cycle, and 256 Mword memory. The machine is cooled by an inert fluorocarbon previously used as a blood substitute.
  • 1986
    • CRAY X-MP with 4 processors achieves 713 MFLOPS (against a peak of 840) on 1000x1000 LINPACK.
    • Alan Karp offers $100 prize to first person to demonstrate speedup of 200 or more on general purpose parallel processor. Benner, Gustafson, and Montry begin work to win it, and are later awarded the Gordon Bell Prize.
  • 1987
    • The first Gordon Bell Prizes for parallel performance is awarded. The recipients are Brenner, Gustafson, and Montry, for a speedup of 400-600 on variety of applications running on a 1024-node nCUBE, and Chen, De Benedictis, Fox, Li, and Walker, for speedups of 39-458 on various hypercubes.
  • 1988
    • John Gustafson and Gary Montry argue that Amdahl's Law can be invalidated by increasing problem size.
    • CRAY Y-MP with 1 processor achieves 74 MFLOPS on 100x100 LINPACK; the same machine with 8 processors achieves 2.1 GFLOPS (against a peak of 2.6) on 1000x1000 LINPACK.
  • 1989
    • CRAY Y-MP with 8 processors achieves 275 MFLOPS on 100x100 LINPACK, and 2.1 GFLOPS (against a peak of 2.6) on 1000x1000 LINPACK.
    • Gordon Bell Prize for absolute performance awarded to a team from Mobil and Thinking Machines Corporation, who achieve 6 GFLOPS on a CM-2 Connection Machine; prize in price/performance category awarded to Emeagwali, who achieves 400 MFLOPS per million dollars on the same platform.
    • Seymour Cray leaves Cray Research to found Cray Computer Corporation.

1990's

  • 1990
    • Cray Research, Inc., purchases Supertek Computers Inc., makers of the S-1, a minisupercomputer compatible with the CRAY X-MP.
    • Gordon Bell Prize in price/performance category awarded to Geist, Stocks, Ginatempo, and Shelton, who achieves 800 MFLOPS per million dollars in a high-temperature superconductivity program on a 128-node Intel iPSC/860. The prize in the compiler parallelization category is awarded to Sabot, Tennies, and Vasilevsky, who achieve 1.5 GFLOPS on a CM-2 Connection Machine with FORTRAN 90 code derived from FORTRAN 77.
    • National Energy Research Supercomputer Center (NERSC) at LLNL places order with Cray Computer Corporation for CRAY-3 supercomputer. The order includes a unique 8-processor CRAY-2 computer system that is installed in April.
  • 1991
    • CRAY Y-MP C90 with 16 processors achieves 403 MFLOPS on 100x100 LINPACK; a Fujitsu VP-2600 with 1 processor achieves 4 GFLOPS (against a peak of 5 GFLOPS) on 1000x1000 LINPACK.
  • 1993
    • Cray Research delivers a Y-MP M90 with 32 Gbyte of memory to the U.S. Government, after delivering a similar machine with 8 Gbyte of memory in the previous year to the Minnesota Supercomputer Center.

References

http://ei.cs.vt.edu/~history/Parallel.html

Vector Machines

First appearing in the 1970s, vector machines were able to apply a single instruction to multiple data values. This type of operation is used frequently in scientific fields or in multimedia.

The Solomon project at Westinghouse was one of the first machines to use vector operations. Its CPU had a large number of ALUs that would each be fed different data each cycle. Solomon was unsuccessful and was cancelled, eventually to be reborn as the ILLIAC IV at the University of Illinois. The ILLIAC IV showed great success at solving data-intensive problems, peaking at 150 MFLOPS under the right conditions.

An innovation came with the Cray-1 supercomputer in 1976. It was realized that the large data sets are often manipulated by several instructions back-to-back, such as an addition followed by a multiplication. In the ILLIAC, up to 64 data points were loaded from memory with every instruction, but had to be stored back to manipulate the rest of the vector. The Cray computer was only able to load 12 data points, but by completing multiple instructions before continuing the total number of memory accesses decreased. The Cray-1 could perform at 240 MFLOPS.

References for this section

Comparing the Data Parallel Model with the Shared Memory and Message Passing Models

Although the shared memory and message passing models may be combined into hybrid approaches, the two models are fundamentally different ways of addressing the same problem (of access control to common data). In contrast, the data parallel model is concerned with a fundamentally different problem (how to divide work into parallel tasks). As such, the data parallel model may be used in conjunction with either the shared memory or the message passing model without conflict. In fact, Klaiber (1994) compares the performance of a number of data parallel programs implemented with both shared memory and message passing models.

As discussed in the previous section, one of the major advantages of combining the data parallel and message passing models is a reduction in the amount and complexity of communication required relative to a task parallel approach. Similarly, combining the data parallel and shared memory models tends to simplify and reduce the amount of synchronization required. If the task parallel code given above were modified from a message passing model to a shared memory model, the two threads would require 8 signals be sent between the threads (instead of 8 messages). In contrast, the data parallel code would require a single barrier before the local sums are added to compute the full sum.

Much as the shared memory model can benefit from specialized hardware, the data parallel programming model can as well. SIMD (single-instruction-multiple-data) processors are specifically designed to run data parallel algorithms. These processors perform a single instruction on many different data locations simultaneously. Modern examples include CUDA processors developed by nVidia and Cell processors developed by STI (Sony, Toshiba, and IBM). For the curious, example code for CUDA processors is provided in the Appendix. However, whereas the shared memory model can be a difficult and costly abstraction in the absence of hardware support, the data parallel model—like the message passing model—does not require hardware support.

Since data parallel code tends to simplify communication and synchronization, data parallel code may be easier to develop than a more task parallel approach. However, data parallel code also requires writing code to split program data into chunks and assign it to different threads. In addition, it is possible that a problem may not decompose easily into subproblems relying on largely independent chunks of data. In this case, it may be impractical or impossible to apply the data parallel model.

Once written, data parallel programs can scale easily to large numbers of processors. The data parallel model implicitly encourages data locality by having each thread work on a chunk of data. The regular data chunks also make it easier to reason about where to locate data and how to organize it.

Definitions

  • Data parallel. A data parallel algorithm is composed of a set of identical tasks which operate on different subsets of common data.
  • Task parallel. A task parallel algorithm is composed of a set of differing tasks which operate on common data.
  • SIMD (single instruction, multiple-data). A processor which executes a single instruction simultaneously on multiple data locations.
  • MIMD (multiple instruction, multiple data). A processor which executes multiple instructions simultaneously on multiple data locations
  • PE A Processing Element
  • PU A Processing Unit (synonymous with PE)
  • FLOPS FLoating point Operations Per Second (a 'benchmark' allowing comparisons between different parallel system architectures)

References

Appendix: C for CUDA Example Code

The following code is a data parallel implementation of the sequential Code 2.3 from Solihin (2008) using C for CUDA. It is presented to give an impression of programming for a SIMD architecture, but a detailed discussion is beyond the scope of this supplement. Ignoring memory allocation issues, the code is very similar to the data parallel example, Code 2.5 from Solihin (2008), discussed earlier. The main difference is the presence of a control thread that sends the parallel tasks to the CUDA device. 

// Data parallel implementation of the example code using C for CUDA.

#include <iostream>

__global__ void kernel(float* a, float* b, float* c, float* local_sum)
{
    int id = threadIdx.x;
    int local_iter = 4;
    int start_iter = id * local_iter;
    int end_iter = start_iter + local_iter;

    // Begin data parallel section

    for (int i = start_iter; i < end_iter; i++)
        a[i] = b[i] + c[i];
    local_sum[id] = 0;
    for (int i = start_iter; i < end_iter; i++)
        if (a[i] > 0)
            local_sum[id] = local_sum[id] + a[i];

    // End data parallel section
}

int main()
{
    float h_a[8], h_b[8], h_c[8], h_sum[2];
    float *d_a, *d_b, *d_c, *d_sum;
    float sum;

    size_t size = 8 * sizeof(float);
    size_t size2 = 2 * sizeof(float);

    cudaMalloc((void**)&d_a, size);
    cudaMalloc((void**)&d_b, size);
    cudaMalloc((void**)&d_c, size);
    cudaMalloc((void**)&d_local_sum, size2);

    cudaMemcpy(d_b, h_b, size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_c, h_c, size, cudaMemcpyHostToDevice);

    kernel<<<1, 2>>>(d_a, d_b, d_c, d_sum);

    cudaMemcpy(h_a, d_a, size, cudaMemcpyDeviceToHost);
    cudaMemcpy(h_sum, d_sum, size2, cudaMemcpyDeviceToHost);

    sum = h_sum[0] + h_sum[1];
    std::cout << sum;

    cudaFree(d_a);
    cudaFree(d_b);
    cudaFree(d_c);
    cudaFree(d_sum);
}
Retrieved from "https://wiki.expertiza.ncsu.edu/index.php?title=CSC/ECE_506_Spring_2011/ch2_cl&oldid=44576"