CSC/ECE 506 Spring 2012/3a kp
Patterns of parallel programming
1. Overview
A design pattern is a description of a solution to a frequently occurring problem in some domain. The description makes it easy for the reader to quickly understand both the problem and the proposed solution. Because the pattern has a name, a collection of patterns provides a vocabulary with which to talk about these solutions. They were first postulated for City Planning applications, but they promptly extended to Computer Science (http://en.wikipedia.org/wiki/Software_design_pattern). The idea would always be to have a library of reusable resources that would help us in the development of our product.
As an example – “Dense Linear Algebra” is a “Computational” design pattern for parallel programming. Under this pattern a computation is organized as a sequence of arithmetic expressions acting on dense arrays of data. The operations and data access patterns are well defined mathematically so data can be prefetched and CPUs execute close to their theoretically allowed peak performance.
Parallel programming design patterns have been identified at various levels of software development from high-level patterns that describe how an application is organized to midlevel patterns about specific classes of computations, and low level patterns describing specific execution strategies. Related to these classifications, there are also available “pattern languages” from several researchers, that guide the software developer through hierarchy of parallel programming design development. (http://www.cise.ufl.edu/research/ParallelPatterns http://parlab.eecs.berkeley.edu/wiki/patterns/patterns).
In this article we first cover two/three of “pattern languages” for parallel programming in some detail. These are attempts to classify them and we then dwell on commonalities between these approaches. Thereafter, we cover a broad range of parallel programming design patterns highlighting the commonalities and differences.
It is important to appreciate that many design problems do not lend themselves to a top-down or bottom-up analysis. In many cases, the pathway through our patterns will be bounce around between layers with the designer working at whichever layer is most productive at a given time.
2. Parallel Pattern Programming Languages
We cover three "Parallel Pattern Programming Languages" and their commonalities.
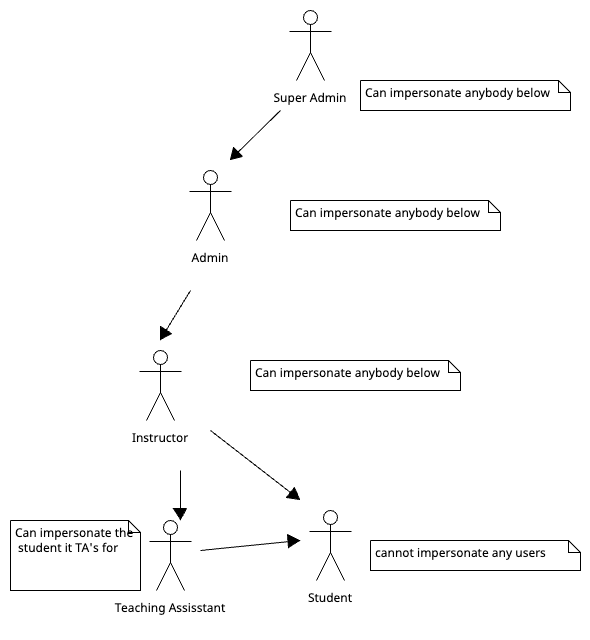
1. A classification developed by B.L.Massingell[ http://www.cise.ufl.edu/research/ParallelPatterns/overview.htm link] considers four levels of patterns - A) FindingConcurrency B) AlgorithmStructure C) SupportingStructures D) ImplementationMechanisms
A) "FindingConcurrency” considers high-level issues to expose potential concurrency. There are three major design patterns at this level – i) Decomposition Strategy pattern - focuses on decomposing the problem into parts that can be run simultaneously and also includes “Task Decomposition pattern” (decomposing into concurrent tasks) and “Data Decomposition pattern” (decomposing into data units that can be run independently). ii) Dependency Analysis – After using "Decomposing Strategy Pattern" to break into entities, the dependency analysis pattern help the programmer understand how they depend on each other. These dependencies include “Grouping Tasks” (to simplify dependency), “Ordering Tasks” (to satisfy constraints) and “Data Sharing” (among tasks). iii) Design Evaluation – This pattern is a consolidation pattern; it is used to evaluate the results of the other patterns in this design space.
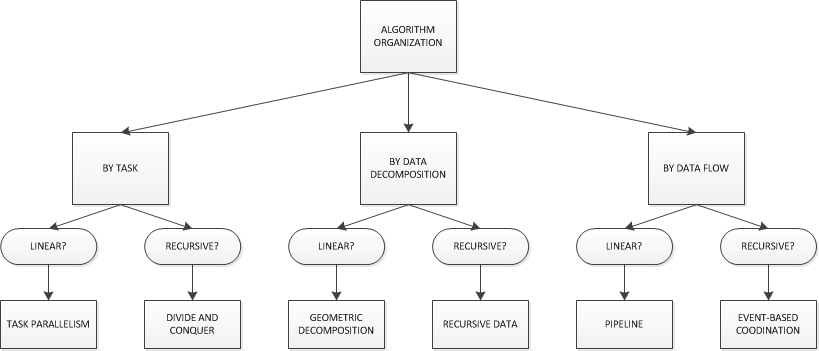
B) Algorithm Structure – This steps moves close to the final program and has six Patterns in three sub-groups - i) Organize by flow of data – Pipeline Processing Pattern (decomposing into ordered tasks groups connected by data dependencies) and Asynchronous Decomposition Pattern(decomposed into task groups that interact through asynchronous events). ii) Organize by tasks – Embarrassingly Parallel Pattern (decomposing into a set of independent tasks) and Divide-and-conquer Pattern (break the problem into subproblems that are solved separately and then recombined later). iii) Organize by data – Geometric Decomposition Pattern (decompose and solve problem into discrete subspaces with the solution for each subspace typically requiring data from a small number of other subspaces) and Recursive Data Pattern (problem is defined in terms of following links through a recursive data structure).