CSC/ECE 506 Spring 2012/ch2b cm

Introduction

This article provides an overview of data parallelism and how modern GPUs (specifically NVidia GeForce Family architecture) exploit it to achieve super computing capabilities. It provides a brief overview of the NVIDIA's Fermi GPU architecture -- Processor hierarchy, Memory hierarchy and Programming model support. The next section introduces the CUDA C programming runtime and the various parallel programming primitives made available by it. This is followed by a discussion of some simple serial(CPU) computing examples that could be expedited by the application of parallel computing techniques.

Why GPUs

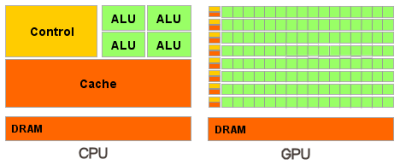
If we look at the modern CPUs and GPUs, and compare their performance (in terms of floating point capability) <ref name=FloatingPoint> http://www.deskeng.com/articles/aaayet.htm </ref>, we notice that GPUs clearly outclass their competitors by a huge margin. This is because GPU is specialized for compute-intensive, highly parallel computation – which is what graphics rendering is all about – and therefore designed such that more transistors are devoted to data processing rather than data caching and flow control (as the following diagram illustrates). Specifically, GPU is best suited for data parallel <ref name=DataParallel>http://en.wikipedia.org/wiki/Parallel_computing#Data_parallelism</ref> applications, with high arithmetic intensity – the ratio of arithmetic operations to memory operations. In such applications where the same set of instructions are executed for each data element, there's minimal need of flow control,while exhibiting high arithmetic intensity. Hence the speed up achieved by super fast parallel arithmatic computations will overshadow the latency incurred by memory accesses and flow control. The following diagram illustrates on a high level, the differences between CPU and GPU architectures.

Terminology

Parallel programming model

A parallel programming model is a concept that enables the expression of parallel programs which can be compiled and executed. The value of a programming model is usually judged on its generality: how well a range of different problems can be expressed and how well they execute on a range of different architectures. The implementation of a programming model can take several forms such as libraries invoked from traditional sequential languages, language extensions, or complete new execution models.

Data parallelism

Data parallelism refers to scenarios in which the same operation is performed concurrently (that is, in parallel) on elements in a source collection or array. Data parallelism with imperative syntax is supported by several overloads of the For and ForEach methods in the System.Threading.Tasks.Parallel class. In data parallel operations, the source collection is partitioned so that multiple threads can operate on different segments concurrently.

Embarrassingly Parallel problems

In parallel computing, an embarrassingly parallel workload (or embarrassingly parallel problem) is one for which little or no effort is required to separate the problem into a number of parallel tasks. This is often the case where there exists no dependency (or communication) between those parallel tasks.

Some Basics

Architecture overview

In this Section , we will discuss the Architecture of GeForce gtx 580 GPU from NVIDIA. The GTX 400/500 series GPU’s are based on NVIDIA’s Fermi Architecture, which has been the most significant leap in terms of Architecture design since the advent of the unified processor designs in the G80s.

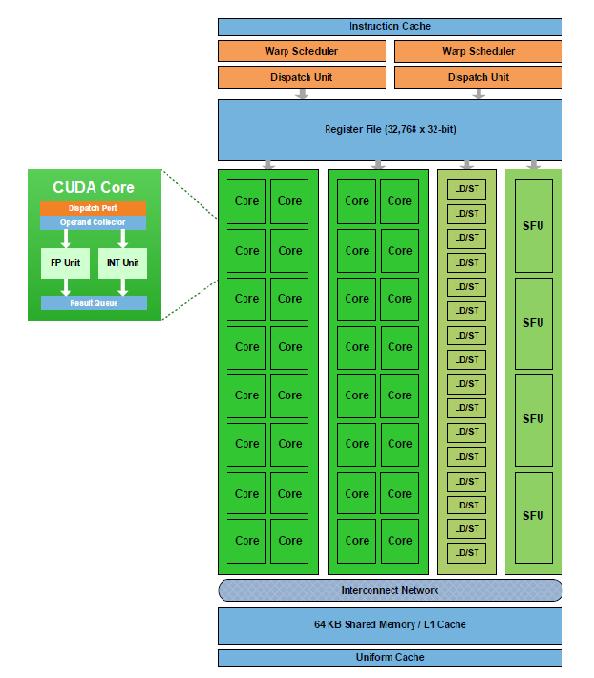
Fermi's GPU Architecture consists of multiple Streaming Multiprocessors (Also referred as Multiprocessors or SMs), each with its own 32 execution cores, as shown in the figure. Typically Fermi hardware has 16 multiprocessors, hence a total of 512 cores (Processing entities -link-). The multiprocessors share an L2 cache, host Interface, GigaThread Scheduler and multiple DRAM interfaces. (-link- details?)

Streaming Multiprocessor

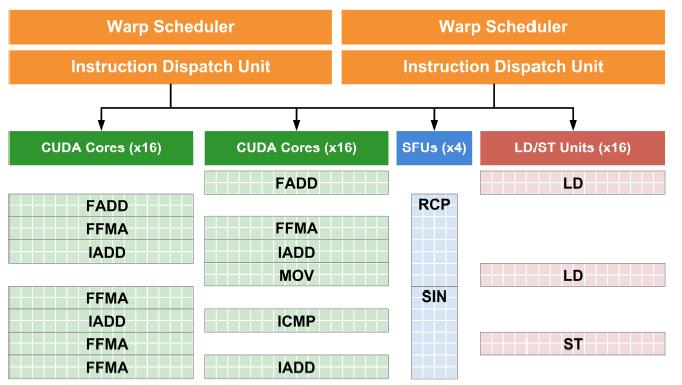
Fermi's third generation Streaming Multiprocessor, consists of 32 CUDA Processors (or cores) that help improve the performance of graphics and compute processing. Each of these 32 cores can perform floating-point and integer operations, with the aid of 16 load-store units for memory operations, four special-function units, and 64K of local SRAM split between cache and local memory. The Multiprocessor provides improved scheduling by using the concept of warps (groups of 32 threads). The SM consists of two warp schedulers and two instruction dispatch units, allowing the two warps to execute simultaneously on the 32 cores. The warps work independently of each other.

Fermi's Fused Multiply ADD(FMA)operation improves the accuracy of the commonly used multiply-add sequences. FMA support also improves the accuracy of other arithmetic operations such as division and square root, and more complex functions such as extended-precision arithmetic, interval arithmetic, and linear algebra.

Memory operations are handled by a set of 16 load-store units in each SM. The load/store instructions can now refer to memory in terms of two-dimensional arrays, providing addresses in terms of x and y values.

A set of four Special Function Units (SFUs) is also available to handle transcendental and other special operations such as sin, cos, exp, and rcp(reciprocal). Four of these operations can be issued per cycle in each SM.

Within the SM, cores are divided into two execution blocks of 16 cores each. Along with the group of 16 load-store units and the four SFUs, there are four execution blocks per SM. In each cycle, a total of 32 instructions can be dispatched from one or two warps to these blocks. It takes two cycles for the 32 instructions in each warp to execute on the cores or load/store units. A warp of 32 special-function instructions is issued in a single cycle but takes eight cycles to complete on the four SFUs.The figure below shows a sequence of instructions being distributed among the available execution blocks.

Cache and Memory Architecture

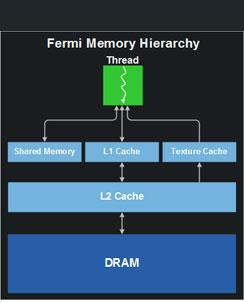
Fermi provides a fully cached memory access with a unified cache architecture that supports graphics and compute programs. Each thread that runs on a single core of a Multiprocessor has access to a super fast texture cache[1], an L1 cache and Shared memory. Each Fermi GPU is also equipped with an L2 cache (768KB in size for a 512-core chip). The L2 cache covers GPU local DRAM as well as system memory. The L2 cache subsystem also implements another feature not found on CPUs: a set of memory read-modify-write operations that are atomic, and thus ideal for managing access to data that must be shared across thread blocks or even kernels. L1 and L2 caches help in improving the random memory access performance while the texture cache enables faster texture filtering -link- . The programs also have access to a dedicated Shared Memory which is a small software-managed data cache attached to each multiprocessor, shared among the cores. This is a low-latency, high-bandwidth, indexable memory which runs essentially at register speeds.

Underneath the hood, the Nvidia GPU was designed to be data-centric, but for a graphics display the data are triangles and textures. The CUDA architecture layer makes the GPU look more processor-like, and more appropriate for general parallel problems.

Programming Model

Fermi's complexity is hidden by a multi-level programming model that allows the programmers to focus on algorithm design, rather than hardware specific details.In NVIDIA’s CUDA software platform, as well as in the industry-standard OpenCL framework, the computational elements of algorithms are known as kernels. Kernels can be written in standard C language, with additional key words to express parallelism. They look similar to C functions, except that they are executed parallely by multiple threads on multiple processing entities.

Threads within a kernel are grouped into Blocks of 1024 threads. This hard limit is imposed by the Fermi hardware which allows a maximum of 1024 threads or 32 warps per thread block. All of the threads in a block will run on a single SM, so within the thread block, threads can cooperate and have access to the shared memory. At hardware level, the 1024 threads within a block are divided into warps of 32 threads (warp is the fundamental unit of dispatch within a single SM). Two warps from different thread blocks may be executed on a single SM, increasing the energy efficiency and hardware utilization. Fermi supports 48 active warps, that is, a total of 48*32, 1536 threads to be active simultaneously on each multiprocessor.

The entire Fermi hardware is available for execution to a single application at any point of time. But the context switch time between the applications is short enough, so that a Fermi GPU can still maintain high utilization even when running multiple applications. This fast switching is enabled by the chip-level GigaThread hardware thread scheduler, which manages 1,536 simultaneously active threads for each streaming multiprocessor across 16 kernels.

Performance tuning on the GPU requires optimizing all these architectural features:

• Finding and exposing enough parallelism to populate all the multiprocessors
• Additional parallelism to allow multithreading to keep the cores busy
• Optimizing device memory accesses for contiguous data
• Utilizing the software data cache (shared memory) to store intermediate results

CUDA C Runtime overview

This section aims to describe basic C programming model provided by NVidia CUDA architecture.

Kernels

As mentioned, Kernels are similar to C functions, except that they are executed N times parallely on N CUDA threads instead of only once like regular C functions. Kernels are declared using __global__ specifier and the number of threads to execute is specified using the "execution configuration" <<<...>>> syntax. Each thread that executes within a kernel is given a unique identifier (obtained using threadIdx variable). Specific examples of using these abstractions follow in the next section.

Thread Hierarchy

Unlike threads in regular Operating systems, CUDA provides programmers to arrange the threads in 1 dimension, 2 dimension and 3 dimension structures called Blocks. Thread blocks and threads each have identifiers (represented by threadIdx,blockIdx variables in CUDA Runtime) that specify their relationship to the kernel. These IDs are used within each thread as indexes to its respective input and output data, shared memory locations, and so on. The threadIdx variable is actually a 3 component vector, i.e threadIdx.x, threadIdx.y, threadIdx.z may be used to access a particular thread (x,y,z) in the 3D block. This provides programmers a natural way to perform parallel computations in domains such as Arrays,Matrices and Volumes.

Blocks in turn can co exist with other blocks of threads, where a group of blocks is termed as Grid. Again blocks can be arranged in 1 dimension, 2 dimension and 3 dimension structures within a Grid and hence enable creation of large number of parallel threads that work in multiple dimensions of data. A thread may access the unique block Id in which it is running by using the variable blockIdx. Thread blocks are required to execute independently: It must be possible to execute them in any order, in parallel or in series. This independence requirement allows thread blocks to be scheduled in any order across any number of cores.

An important requirement of a parallel programming model is providing a way to synchronize between the threads. CUDA allows this barrier synchronization in the Kernel using the light weight __synthreads() function.

Memory Hierarchy

As mentioned above, memory access latency is not a major concern for data parallel applications. But still a good architecture strives to provide fast, efficient memory access to thousands of threads that run in parallel. In CUDA, each thread has access to local memory and a super fast shared memory, visible to all threads within a block and with same lifetime as the block. CUDA runtime allows shared memory allocation using the __shared__ qualifier. All threads also have access to a global device memory which is somewhat slower. There are also two additional read-only memory spaces accessible by all threads: the constant and texture memory spaces, which are optimized for different memory usage patterns. The global, constant, and texture memory spaces are persistent across kernel launches by the same application.

Kernels can only operate out of device memory (no access to Host memory), so the runtime provides functions to allocate, deallocate, and copy device memory, as well as transfer data between host memory and device memory. Device memory can be allocated either as linear memory or as CUDA arrays (optimized for texture fetching -link-). Linear memory on device exists in a 32 bit address space, so separately allocated entities can reference one another via pointers, e.g in a linked list. Linear memory is allocated using cudaMalloc() and freed using cudaFree() and data transfer between host memory and device memory are performed using cudaMemcpy().Linear memory can also be allocated through cudaMallocPitch() and cudaMalloc3D(). These functions are recommended for allocations of 2D or 3D arrays as it makes sure that the allocation is appropriately padded to meet the alignment requirements, ensuring the best performance when accessing and performing copies of 2D or 3D arrays.

Traditional Problem

Following is a most elementary problem that illustrates the essence of data parallelism. It involves computing the addition of two vectors and storing the result into a third vector. A standard C program to achieve this would look like this:

int main()
{
	float A[1000],B[1000],C[1000];
	.....	
	//Some initializations
	.....

	for(int i = 0; i < 1000; i++)
		C[i] = A[i] + B[i];

	......
}

Here we are executing the for loop, once for each array index. On a sequential processor (Single core processor),the instructions similar to the following are executed for each run of the for loop.

Fetch i
Fetch A[i] into Register EAX
Fetch B[i] into Register EBX
Add EBX to EAX
Store EAX into Adress of C[i]

Hence the time taken to perform this simple computation is linear in the size of the input. This could manifest as a major bottleneck in real time applications such as 3D renderings, Face recognition, Monte Carlo simulation,etc where the input to be processed is embarrassingly large.

Solution

The pattern that exists in all of these problems is that, there's one instruction or a single set of instructions that act on a large amount of distinct data elements (SIMD [2]). This is a typical pattern where data parallelism can be applied.

In a two processor (or two core) system, we could have both the processing units (cores) work on a part of the array simultaneously. Following snippet is a rough outline of how this could be achieved:

.....
    if CPU = "a"
       lower_limit := 0
       upper_limit := round(A.length/2)
    else if CPU = "b"
       lower_limit := round(A.length/2) + 1
       upper_limit := A.length

for i from lower_limit to upper_limit by 1
   C[i] = A[i] + B[i];
.....

This is typically done in high level programming languages such as C using the Thread[3] abstraction, where each thread runs simultaneously on a different processing unit. Even though this solution is much faster, it is still limited to just two parallel executions.

GPU solution

Because the same program (set of instructions) is executed for each data element, there is a lower requirement for sophisticated flow control, and because it is executed on many data elements, it exhibits high arithmetic intensity. GPU is specialized for compute-intensive, highly parallel computation – exactly what graphics rendering is about – and therefore designed such that more transistors are devoted to data processing rather than data caching and flow control. Hence GPU (more specifically CUDA) would be the best answer to such a problem.

Similar to what we did with the two processor, multi-threaded solution, CUDA enables us to create thousands of threads and run them parallely on thousands of Processing units that GPU provides. Following C program illustrates how this can be achieved:

__global__ void VecAdd(float* A, float* B, float* C)
{
	int i = threadIdx.x;
	C[i] = A[i] + B[i];
}

int main()
{
	...
	// Invocation with N threads
	VecAdd<<<1, 1000>>>(A, B, C);
	...
}

In this code, the main function simply calls a specialized routine (called Kernel [4]), and passes in the 3 arrays that need to be processed parallely. It also informs the CUDA runtime [5] to create 1000 threads, where each thread runs the same VecAdd routine, but on different data. As can be seen from the code, in the VecAdd routine, we are finding the thread index and acting only on that index of the input arrays. Hence each of the 1000 threads acts on a different location and performs the computation. This helps us achieve exponential performance improvements, which becomes evident when dealing with super-parallel applications such as those mentioned above.

Slightly Evolved Problem

Let us increase slightly the complexity of the above problem. Consider the program that adds two NxN matrices. A simple CPU program to achieve this may look like this:

void add_matrix( float* a, float* b, float* c, int N ) 
{ 
	int index; 
	for ( int i = 0; i < N; ++i ) 
	for ( int j = 0; j < N; ++j ) 
	{ 
		index = i + j*N; 
		c[index] = a[index] + b[index]; 
	} 
} 
 
int main() 
{
    add_matrix( a, b, c, N );
}

As discused before, CUDA provides a hierarchy of threads, which can be exploted to achieve fast parallel computation in 2D and 3D as well. In order to achieve data parallelism in 2D or 3D, we can use the 3 components (x,y,z) of threadIdx variable.For a two-dimensional block of size (Dx, Dy), the thread ID of a thread of index (x, y) is (x + y Dx); for a three-dimensional block of size (Dx, Dy, Dz), the thread ID of a thread of index (x, y, z) is (x + y Dx + z Dx Dy). Based on this idea, the following code adds two NxN matrices in parallel:

__global__ void MatAdd(float A[N][N], float B[N][N],float C[N][N])
{
	int i = threadIdx.x;
	int j = threadIdx.y;
	C[i][j] = A[i][j] + B[i][j];
}
int main()
{
	...
	// Invocation with one block of N * N * 1 threads
	int numBlocks = 1;
	dim3 threadsPerBlock(N, N);
	MatAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
	...
}

MatAdd kernel here performs the N*N additions almost at the same time, assuming the GPU has so many processing entities. Hence the performance boost obtained is easily exponential as compared to regular CPU computation.

Some interesting Applications

• IBM Watson

IBM Watson[6] has established itself as one of the fastest super computers by competing against best human players in the game of Jeopardy. If executed on a single core, it takes it approximately 2 hours to answer a single Jeopardy question. But the "real IBM Watson" with 2880 cores performs the same task in less than 3 seconds.

• Password guessing [7]

Technological attacks involve using computers to guess passwords. This is typically accomplished by having the computer try every possible password until it finds the correct one. Advances in GPUs have enabled brute force attacks to be executed faster than ever, hence making this a major security challenge.

• Air traffic control

Rapid prediction of aircraft trajectories is critical for decision making in future Trajectory Based Operations. GPU computing allows you to exploit the parallelism in the trajectory prediction process to have extremely fast run-times. This in turn allows you to achieve real-time performance and analyze models with greater complexity.

References

<references />

Questions

1.What advantage does CPU have over GPU?

2.Name the Latest GPU whose Architecture is discussed in this article.

3.How many CUDA Processors are present in the NVIDIA Fermi Architecture?

4.How are kernels in CUDA Programming different from normal C functions?

5.What are the different memory spaces provided by the CUDA Architecture?

6.How does SIMD work?

7.What is an Embarrassingly Parallel Problem?

8.Can a thread block be three dimensional?

9.If Yes, How do you access a specific thread in a block?

10.Name one interesting research happening in Parallel Computing.