CSC/ECE 506 Spring 2015/5b SA

Introduction

Parallelization of computations in the presence of dynamic data structures has shown immense potential. Here we discuss how can we parallelize linked data structures ^[7]. Efficiently exploiting parallelism is fundamental in parallel computing even in the context of dynamic data structures. Some amount of speculation is needed to figure out how to exploit it the best. The idea is to introduce concurrency^[6] in the existing data structures to enable multi-threading and hence parallelism. We need to handle synchronization since we need concurrency. We discuss the major steps in parallelizing data structures and then discuss some techniques and algorithms existing in the literature to gain more insight into the process.

Overview

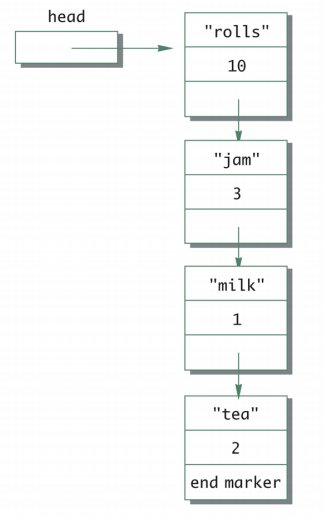
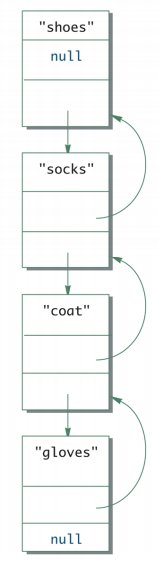
The simplest linked data structure we can think of is a linked list. A single linked list with one pointer pointing to the next node in the list or double linked list where nodes have two pointers pointing to the adjacent nodes to its left and right in the linked list are the most commonly used linked data structures. Following figures are some examples of the same. The first shows the head node to a singly linked list and the second shows a double linked list.

[1]

Linearizability

Linearizability is an important property of operations that may be executed concurrently [Herlihy and Wing(1990)]^[3][2]. An operation executed by some processor is linearizable if the rest of the system observes the corresponding system state change as if it occurred instantaneously at a single point in time after the operation started and before it ﬁnished. This property ensures that all the linearizable operations in the program have a mutual order observed in the same way by the entire system.

As mentioned before concurrency needs to be enabled for parallel linked data structures. In that context, linearizability is a useful property to have for concurrent operations. It can identify a single instruction or sub-operation which changes the data structure state and is known to be itself linearizable. In example 1, we will identify (Compare-and-Set) CAS instructions as linearization points.

Linked Data Structure parallelization

Unlike data structures like arrays, linked lists are unsuitable for naive parallelization methods which employ divide and conquer policy, they split the input and assign them to multiple workers for parallel processing. Splitting an arbitrary linked list requires traversing half of its elements. For too many operation instances such an O(n) splitting is unacceptable. Hence, intuitively, it is more efficient to convert the linked list into an array and then use splitters on the array. One thing to be noticed is that these data structures does not retain information about the relative order of elements, hence the operators applied to their data-parallel operations need to be commutative.

As mentioned before, a linked list data structure consists of a set of nodes such that each node points to another node in the set. A special node in this set is considered to be the head of the linked list. We consider connected linked lists without loops, which means every node can be reached from the head, no two nodes point to the same node and no node points at the root.

Example 1 LOCK FREE Parallelized Linked List

The following code snippet shows a parallelized linked list. [3]

:class Invocation[T](xs: List[T]) {
::@volatile var stack = xs
::def READ = unsafe.getObjectVolatile(this, OFFSET)
::def CAS(ov: List[T], nv: List[T]) = unsafe.compareAndSwapObject(this, OFFSET, ov, nv)
:}

:abstract class ListTask[T] extends RecursiveTask[T] {
::val inv: Invocation[T]
::def workOn(elem: T): Unit
::def compute() {
::: val stack = inv.READ
::: stack match {
:::: case Nil =>
::::// no more work
::: case head :: tail =>
:::: if (inv.CAS(stack, tail)) workOn(stack)
:::: compute()
:::}
::}
:}

:class ListForeach[T, U](f: T => U, val inv: Invocation[T]) extends ListTask[T] {
:: def workOn(elem: T) = f(elem)
:}

:implicit class ListOps[T](val par: Par[List[T]]) {
::def foreach[U](f: T => U) = {
:::val inv = new Invocation(par.seq)
:::val tasks = for (i <- 0 until P) yield new ListForeach[T](f, inv)
:::for (t <- tasks) t.fork()
:::for (t <- tasks) t.join()
::}
:}

^[11] and ^[12] discuss mutex/lock free parallelization of linked data structures which more in vogue now.

In the above code snippet, the linked list itself is considered as a stack of elements. In the concrete example above the immutable Lists from the Scala standard library has been used. Since, multiple workers will work on the elements of this list, we need to have atomic read and Compare-and-Set or CAS operations.

The JVM deﬁnes volatile variables the writes to which are immediately visible to all other threads. In Java these variables are deﬁned with the volatile keyword before the declaration, and in Scala with the @volatile annotation. Whenever we read a volatile variable x, the notation READ(x) is used in the pseudocode, to make it explicit that this read is atomic, i.e. it can represent a linearization point. When writing the value v to the volatile variable, the notation WRITE(x, v) is used. A special compare-and-set or CAS instruction atomically checks if the target memory location is equal to the speciﬁed expected value and, if it is, writes the new value, returning true. Otherwise, it returns false. It is basically equivalent to the corresponding synchronized block, but more eﬃcient on most computer architectures.

The stack is manipulated using atomic READ and CAS operations to ensure that every element is assigned to exactly one worker. After reading the stack ﬁeld in line val stack = inv.READ , every worker checks whether it is empty, indicating there is no more work. If the list is non-empty, every worker attempts to replace the current list by its tail with the CAS line if (inv.CAS(stack, tail)) workOn(stack). Success means that only that worker replaced, so he gains ownership of that element – he must call workOn to process the element. If the CAS is not successful, the worker retries by calling the tail-recursive compute again. The algorithm is correct – a successful CAS in line 89 guarantees that the stack ﬁeld has not changed its value since the READ in line 84. No linked list suﬃx will ever appear more than once in the ﬁeld stack because there are no more loops in the linked list when following the tail pointer. Furthermore, every linked list node will appear in the stack ﬁeld at least once since the list is connected. Together, these properties ensure that every linked list element is assigned to exactly one worker.

The algorithm shown in above is lock-free – although many threads compete to update the ﬁeld stack at the same time, after a certain ﬁnite number of steps some thread will always complete its operation. In general this number of steps can depend on the size of the data structure or the number of competing workers, but in this case the number of steps is constant and equals the number of instructions between two consecutive CAS calls. In the next example #Example 2 LOCK based Parallelized Queue Linked List we show parallelization through mutex locks.

Example 2 LOCK based Parallelized Queue Linked List

Now, lets consider the queue data structure based on single linked list. The following code snippet explains a parallelized queue. ^[4] ^[5]

#include <pthread.h>

#include <list.h> // you could use std::list or your implementation

namespace concurrent { template <typename T>

class Queue {

public:

 Queue( ) { 
    pthread_mutex_init(&_lock, NULL); 
 } 
 ~Queue( ) { 
   pthread_mutex_destroy(&_lock);
 } 
 void push(const T& data);
 T pop( );

private:

 list<T> _list; 
 pthread_mutex_t _lock;

} };

Multiple threads of control can simultaneously try to push data to the queue or remove data, so we need a mutex object to manage the synchronization. The constructor and destructor of the queue class are responsible for the creation and destruction of the mutex, as shown above.

For insertion and deletion of data from a concurrent queue, we need mutex locks. What happens if multiple threads intend to append data to the queue? The first thread locks the mutex and appends data to the queue, while the other threads wait for their turn. The operating system decides which thread adds the data next in the queue, once the first thread unlocks or releases the mutex. By default, there is no real time priority threads, the thread waiting the longest is the next to wake up, acquire the lock, and append the data to the queue. Below snippet shows insertion:

procedure: Pushing data to the queue

void Queue<T>::push(const T& value ) {

:      pthread_mutex_lock(&_lock);
:      _list.push_back(value);
:      pthread_mutex_unlock(&_lock);

}

The code for popping data out is similar. Below code snippet shows:

Procedure: Popping data from the queue

T Queue<T>::pop( ) {

:      if (_list.empty( )) { 
:          throw ”element not found”;
:      }
:      pthread_mutex_lock(&_lock); 
:      T _temp = _list.front( );
:      _list.pop_front( );
:      pthread_mutex_unlock(&_lock);
:      return _temp;

}

As seen from the above snippets, locking is done before pushing and popping and release locks after the operations are done. However, if we have a long queue, and there are significantly more threads reading data out of the queue than those appending data at some point during code execution, the read speed is slowed down as per the above implementation. The reason is we are sharing the same mutex for push and pop operations. The writer threads access the lock, hence reads are inhibited. Can we use two locks? One for the read operation and another for the write should do the trick. Following snippet, shows the modified version of more efficient concurrent queue using two locks instead of one:

template <typename T> class Queue { public:

  Queue( ) { 
      pthread_mutex_init(&_rlock, NULL); 
      pthread_mutex_init(&_wlock, NULL);
   } 
   ~Queue( ) { 
      pthread_mutex_destroy(&_rlock);
      pthread_mutex_destroy(&_wlock);
   } 
   void push(const T& data);
   T pop( );

private:

   list<T> _list; 
   pthread_mutex_t _rlock, _wlock;

}

Pop and push snippets shown below are modified using two distinct locks, one for read and the other for write:

void Queue<T>::push(const T& value ) {

      pthread_mutex_lock(&_wlock);
      _list.push_back(value);
      pthread_mutex_unlock(&_wlock);

}
T Queue<T>::pop( ) {

      if (_list.empty( )) { 
          throw ”element not found”;
      }
      pthread_mutex_lock(&_rlock);
      T _temp = _list.front( );
      _list.pop_front( );
      pthread_mutex_unlock(&_rlock);
      return _temp;

}

Now, as we discussed the mutex lock based approach, it possesses some problems:

Waiting on mutexes consumes considerable time. This delay though have negative effects on system scalability.
Lower-priority threads could acquire a mutex, thus halting higher-priority threads that require the same mutex to proceed. This problem is known as the famous priority inversion. ^[8]
A thread holding a mutex can be de-scheduled, perhaps because it was the end of its time-slice. For other threads waiting on the same mutex, this has a negative effect, because the wait time is now even longer. This problem is known as lock convoying. ^[9]

Thus, issues with mutexes has compelled developers to come up with solutions that donot use mutexes like the Compare and swap (CAS) synchronization primitive used in #Example 1 LOCK FREE Parallelized Linked List. Although mutexes are tricky to use, they are definitely worth our attention better performance.

This section provides some insights to the designing of parallelized linked data structures that are amenable to concurrent access. As seen, the design choices could be mutex based or lock-free. Either way, both require ways of thinking that go beyond the traditional functionality of these data structures. We need to be aware of preemption and how the thread resumes when it is rescheduled. At this juncture the solution on the lock-free side of things are more platform/compiler oriented. The Boost library for an implementation of threads and locks and John Valois's paper on lock-free linked lists provide ways to implement in a lock-free way. ^[11] ^[12] can be referred for more pointers.

Algorithms

There are several parallelization techniques possible for linked lists. But, each data structure needs to be reviewed on a per-case basis. This means a programmer needs to assess the codes carefully before deciding on which parallelization strategy is best applicable.

After parallelism is identified, programs can be parallelized and then executed on parallel multiprocessor systems to achieve good performance. Good compiler analysis techniques can only analyze parallelism in the traversal operations in programs with dynamic pointer-linked data structures. As a result, only the traversal operations will be parallelized while the construction operations will be executed in sequential. Although the traversal phase of such programs, which usually account for over 90% of total execution times, can be parallelized, the rest of programs that accounts for less than 10% will dominate the execution on multiprocessor systems.[4]

Let us now look at a few algorithms for achieving parallelism in different Linked Data Structures:

Simple Locks

The most easy and intuitive approach to parallelization is to parallelize the traversal of LDS. There are no conflicts between Reads among different threads in a Data Structure. Next, we try to introduce parallelism among the different construction operations – Add and Delete. This means that while different threads can simultaneously operate on two different parts of the Data Structure, no two threads will operate on a single(or adjacent) nodes at the same time.

This approach gives rise to the implementation of locks. Locks can be used to define a critical section, which can only be accessed by one thread at a time. Fundamentals of Parallel Computer Architecture very well defines the techniques for implementing a lock on a simple LDS – the linked list. We will not go through the details, as our focus remain on the techniques not introduced before:

Readers Lock

In this technique, we implement a Read Lock and a Write Lock. A Traversal Operation must obtain a Read Lock prior to execution, and a Modify Operation must obtain a Write Lock prior to execution. Both must release locks after completion. When a Read Lock is granted to an operation, a request for another Read Lock can be granted, but a request for Write Lock cannot be granted until all Read Locks have been released. Finally, if a Write Lock is granted to an Operation no requests for Read or Write Locks will be granted until the operation has completed execution and released the lock.

Global Lock

This technique is fairly easy to implement, as it contains only one global lock for the entire Linked Data Structure. As before, threads can traverse the LDS in parallel and identify the node they want to modify. To Modify(add/delete), each thread must acquire a Global Lock. As every thread contends for only one global lock, there is no possibility of deadlocks or livelocks. This approach has enabled us to increase the degree of parallelism by getting rid of Read Locks. However, we still have more scope of parallelism as modification operations can also execute in parallel as long as they are not on the same or adjacent nodes.

Fine Grain Lock

This technique implements a Read Lock and Write Lock for each node. A node that is read and must remain valid for other operations to complete must be Read Locked. A node that is to be modified must remain Write Locked. In this approach, multiple nodes may be read and modified in parallel, but each node has locks which allows only one thread to manipulate it at a time.

The Cyclic Graph Parallelization

-http://www.iis.sinica.edu.tw/PARALLEL/cthpc/7th/18CTHPC01.pdf- gives an approach that can identify parallelism based on data dependence and shape analysis on programs even with cyclic graphs. If traversal operations on pointer-linked data structures in a program can be executed in any order, it implies the nodes of the traversed data structures can be connected in any order. Parallelism in construction( Modify) operations exists if this condition holds, i.e. nodes of pointer-linked data structures in the program can be connected in any order. One typical example is the list representation of adjacent matrixes, each of which can represented by a list of lists. The lists of such a list of lists can be built independently.

The technique can be divided into the following steps:

1. Compute definition - use chains

Each traversal operation corresponds to a read reference on pointer-linked data structures, while each construction operation corresponds to a write reference. Commonly, people refer to a read reference as use and to a write reference as definition, the relationships between construction operations and traversal operations of dynamic pointer-linked data structures can be represented by definition-use chains of the data structures. http://www.cs.rice.edu/~keith/512/2009Lectures/11DUChains.pdf

2. Recognize parallelism in traversal operations

As mentioned above, if we're able to identify parallelism in the traversal operation such that traversal can take place in any order within the Cyclic graphs, then this means that we can modify the graph in any order. However, if there is no parallelism among the traversal techniques, we might have to follow the serial ordering for construction operations.

3. Identify parallelism in construction operations

With the use of Locks, ensure that each Construction operation can be executed in parallel with respect to another operation. A node may not be allowed to be modified before a thread has completed an operation on it.

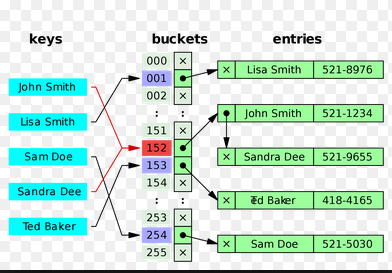
Hash Tables

http://pages.cs.wisc.edu/~remzi/OSTEP/threads-locks-usage.pdf- Now let us focus on algorithms for a hash table. Note that a hash table works in key-value pairs as shown below:

Let us begin with the code snippet for implementing Parallelization of a simple fixed Hash Table:

#define BUCKETS (100) 

typedef struct __hash_t { 
  list_t lists[BUCKETS]; 
} hash_t; 

void Hash_Init(hash_t *H) { 
  int i; 
  for (i = 0; i < BUCKETS; i++) { 
     List_Init(&H->lists[i]); 
  } 
}

The above code initializes the fixed data structure. Here, each data structure initialization is assigned to a set of lists. These can later be accessed with the use of keys. Here, each instantiated object can contain upto a hundred elements.

int Hash_Insert(hash_t *H, int key) { 
  int bucket = key % BUCKETS; 
  return List_Insert(&H->lists[bucket], key); 
} 

int Hash_Lookup(hash_t *H, int key) { 
  int bucket = key % BUCKETS; 
  return List_Lookup(&H->lists[bucket], key); 
}

Here, an example of a Modify Operation (Hash_Insert) and a Traversal Operation (Hash_Lookup) is given. Each data structure has a list, whose values can be accessed using a key.

The key point here is that this hash table can be implemented using a concurrent linked list, which we have come across numerous times. An example code of the Linked List is shown below.

// basic node structure 
typedef struct __node_t { 
  int key; 
  struct __node_t *next; 
} node_t; 

// basic list structure (one used per list) 
typedef struct __list_t { 
  node_t *head; 
  pthread_mutex_t lock; 
} list_t; 

void List_Init(list_t *L) { 
  L->head = NULL; 
  pthread_mutex_init(&L->lock, NULL); 
} 

int List_Insert(list_t *L, int key) { 
  pthread_mutex_lock(&L->lock); 
  node_t *new = malloc(sizeof(node_t)); 
  if (new == NULL) { 
    perror("malloc"); 
    pthread_mutex_unlock(&L->lock); 
    return -1; // fail 
  } 
  new->key = key;
  new->next = L->head; 
  L->head = new; 
  pthread_mutex_unlock(&L->lock); 
  return 0; // success 
}

int List_Lookup(list_t *L, int key) { 
  pthread_mutex_lock(&L->lock); 
  node_t *curr = L->head; 
  while (curr) { 
    if (curr->key == key) { 
      pthread_mutex_unlock(&L->lock); 
      return 0; // success 
    } 
    curr = curr->next; 
  } 
  pthread_mutex_unlock(&L->lock);
  return -1; // failure 
}

This data structure is parallelized by representing each hash bucket as a list, and using a lock per hash bucket. Hence, implementing a data structure using a LDS has helped create a Concurrent Hash Table.

PLDS

Use cases and Applications

Conclusions

References

1. http://idb.csie.ncku.edu.tw/tsengsm/COURSE/Java/Slides/Java-15-Linked_Data_Structure.pdf

2. http://axel22.github.io/resources/docs/my_thesis.pdf

3. http://dl.acm.org/citation.cfm?id=78972 Maurice Herlihy and Jeannette M. Wing. Linearizability: A correctness condition for concurrent objects. ACM Transactions on Programming Languages and Systems, 12(3):463–492, July 1990.

4. http://www.ibm.com/developerworks/aix/library/au-multithreaded_structures1/#list2

5. http://www.ibm.com/developerworks/aix/library/au-multithreaded_structures2/

6. http://en.wikipedia.org/wiki/Concurrent_data_structure

7. http://en.wikipedia.org/wiki/Linked_data_structure

8. http://en.wikipedia.org/wiki/Priority_inversion

9. http://en.wikipedia.org/wiki/Lock_convoy

10. http://dl.acm.org/citation.cfm?id=2086717&dl=ACM&coll=DL - Partitioning linked data structures for parallelism by Min Feng, Changhui Lin, Rajiv Gupta

11. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.41.9506 - Lock-Free Linked Lists Using Compare-and-Swap by John D. Valois

12. http://www.cl.cam.ac.uk/research/srg/netos/lock-free/ - Practical lock-free data structures

CSC/ECE 506 Spring 2015/5b SA

Contents

Introduction

Overview

Linearizability

Linked Data Structure parallelization

Example 1 LOCK FREE Parallelized Linked List

Example 2 LOCK based Parallelized Queue Linked List

Algorithms

Simple Locks

The Cyclic Graph Parallelization

Hash Tables

PLDS

Use cases and Applications

Conclusions

References

Navigation menu

CSC/ECE 506 Spring 2015/5b SA

Introduction

Overview

Linearizability

Linked Data Structure parallelization

Example 1 LOCK FREE Parallelized Linked List

Example 2 LOCK based Parallelized Queue Linked List

Algorithms

Simple Locks

The Cyclic Graph Parallelization

Hash Tables

PLDS

Use cases and Applications

Conclusions

References

Navigation menu

Search