CSC/ECE 506 Spring 2012/ch5a ja
Chapter 5a CSC/ECE 506 Spring 2012 / ch5a
An exploration and summary of concurrency issues as it relates to linked-list based data structures such as hash tables, trees, and graphs. This topic examines concurrency problems related to each type and possible solutions to allow for parallelization.
Introduction to Linked-List Parallel Programming
One component that tends to link together various data structures is their reliance at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket, trees have linked lists with left and right tree nodes, and graphs have linked lists to determine shortest path algorithms.
But what mechanism allows us to generate parallel algorithms for these structures?
For an array processing algorithm, a common technique used at the processor level is the copy-scan technique. This technique involves copying rows of data from one processor to another in a log(n) fashion until all processors have their own copy of that row. From there, you could perform a reduction technique to generate a sum of all the data, all while working in a parallel fashion. Take the following grid:[1]
The basic process for copy-scan would be to:
Step 1) Copy the row 1 array to row 2. Step 2) Copy the row 1 array to row 3, row 2 to row 4, etc on the next run. Step 3) Continue in this manner until all rows have been copied in a log(n) fashion. Step 4) Perform the parallel operations to generate the desired result (reduction for sum, etc.).
But how does this same process work in the linked list world?
With linked lists, there is a concept called pointer doubling, which works in a very similar manner to copy-scan.[1]
Step 1) Each processor will make a copy of the pointer it holds to it's neighbor. Step 2) Next, each processor will make a pointer to the processor 2 steps away. Step 3) This continues in logarithmic fashion until each processor has a pointer to the end of the chain. Step 4) Perform the parallel operations to generate the desired result.
However, with linked list programming, similar to array-based programming, it becomes imperative to have some sort of locking mechanism or other parallel technique for critical sections in order to avoid race conditions. To make sure the results are correct, it is important that operations can be serialized appropriately and that data remains current and synchronized.
In this chapter, we will explore 3 linked-list based data structures and the concurrency issues they present: hash tables, trees, and graphs.
Linked Data Structure algorithms extension
Lock free algorithms
In order to overcome the ABA problems (shown in figure blow), we add auxiliary nodes to the data we structure. An auxiliary node is a cell that contains only a next field. We require that every normal cell in the list have an auxiliary node as its predecessor and as its successor. We permit “chains” of auxiliary nodes in the list (i.e., we do not require that every auxiliary node have a normal cell as its predecessor and successor), although such chains are undesirable for performance reasons.[7]
The list also contains two dummy cells as the first and last normal cells in the list. These two cells are pointed at by the root pointers First and Last. These dummy cells need not, respectively, be preceded and followed by auxiliary nodes. Thus, m empty list data structure consists of these two dummy cells separated by an auxiliary node.
A cursor is implemented as three pointers into the data structure: target is a pointer to the cell at the position the cursor is visiting. If the cursor is visiting the end-of-list position, then target will be equal to Last. The pointer pre-aux points to an auxiliary node in the data structure. For a cursor c, if c“.pre-aux = c“.target, then the cursor is valid; otherwise it is invalid. The pointer pre.cell points to a regular cell in the data structure. This pointer is used only by the TRYDELETE operation described below. An invalid cursor indicates that the structure of the list in t he vicinity of the cursor has changed (due to a concurrent insert ion or deletion by another process) since the pointers in the cursor were last read. The UPDATE algorithm, given in Figure 5, examines the state of the list and updates the pointers in the cursor so that it becomes valid. Since the list structure contains auxiliary nodes (perhaps more than one in a row), the UPDATE algorithm must skip over them. If two adjacent auxiliary nodes axe found in the list, the UPDATE algorithm will remove one of them.
Traversal of the list data structure is accomplished by using the FIRST and NEXT operations, which use the UPDATE operation. Algorithms are given in Figures 6 and 7. The NEXT operation returns FALSE if the cursor is already at the end of the list and cannot be advanced. Adding new cells into the list requires the insertion of both the cell and a new auxiliary node. This insertion is restricted to occur in the following way: The new auxiliary node will follow the new cell in the list, and insertion can only occur between an auxiliary node and a normal cell, as shown in Figure 8.
Figure 9 gives an algorithm, which takes as arguments a cursor and pointers to a new cell and auxiliary node. The algorithm will try to insert the new cell and auxiliary node at the position specified by the cursor, returning the value TRUE if successful.
If the cursor becomes invalid, then the operation returns without inserting the new cell and returns the value FALSE. This allows a higher-level operation to detect that a change to the structure of the list occurred and to take it into account before attempting to insert the new cell again. For example, in the next section we show how the items in the list can be kept sorted using this technique.
Given a valid cursor, the cell that it is visiting can also be deleted from the list. As with the insertion of new cells, if the list structure changes (i.e., the cursor becomes invalid) then the operation fails and must be tried again. Figure 10 gives the TRYDELETE algorithm. The deletion of the cell from the list leaves an “extra” auxiliary node; concurrent processes deleting adjacent cells can result in longer chains. Most of the TRYDELETE algorithm is concerned with removing the extra auxiliary nodes from the list. Normally, removing the extra auxiliary node that results from the deletion of a cell from the list is accomplished by simply swinging the pointer in the cell pointed at by the pre-cell pointer in the cursor.
However, this does not always work; in particular, this cell may have itself been deleted from the list, in which case swinging its next pointer will not remove the extra auxiliary node: In order to overcome this problem, we add a back~ink field to the normal cells in the list. When a cell is deleted from the list, the pre.cell field of the cursor is copied into the cell’s backdink field. The TRYDELETE algorithm can then use these pointers to reverse back to a cell that has not been deleted from the list.
With just two processes, it is possible to create a chain of auxiliary nodes (with no intervening normal cells) of any length. However, any such chain can exist in the list only as long as some process is executing the TRYDELETE algorithm.
If all deletions have been completed, then the list will contain no extra auxiliary nodes. To see this, assume that there is a chain of two or more-+ auxiliary nodes in the list. Let z be the normal cell that was deleted from between the first two auxiliary nodes in the chain. Note that this implies that the normal cell that immediately preceded x in the list has not been deleted. By assumption, the operation that deleted z has completed. Consider the loop at lines 17–21 of the TRYDELETE algorithm. The only way for the process to exit this 100P, and hence to complete the operation, is for another deletion operation to have extended the chain of auxiliary nodes by deleting the normal cell g immediately following the chain, since the cell z is at the front of the chain. Furthermore, the deletion of y must have occurred after the operation deleting x had set its back_link pointer at line 6; otherwise the auxiliary node following y would have been included in the chain found in lines 13–16. Thus, the chain of back_link pointers followed by the process that deleted y will lead to the same normal cell that preceded x.
Now, the only way for the operation that deleted y to have completed is for the same reason as above; i.e., another TRYDELETE operation must extend the chain of auxiliary nodes by deleting a cell z. Since the length of the list must be finite, there must be a last such deletion which, but by the argument above, cannot have completed. Thus this operation must still be in progress, contradicting the assumption that there were no TRYDELETE operations in progress.
Trees
This chapter gives a serial code for a tree traversal, and a parallel solution to implement same function.
Serial Code Example
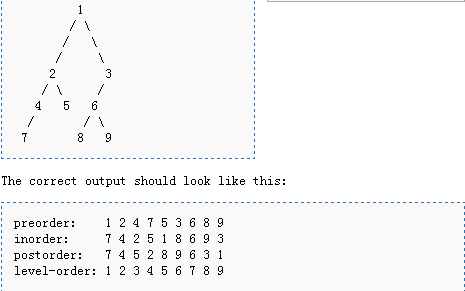
Below is a code[7] for tree traversal algorithms its behavior is as figure below shows:
procedure Tree_Traversal is
type Node;
type Node_Access is access Node;
type Node is record
Left : Node_Access := null;
Right : Node_Access := null;
Data : Integer;
end record;
procedure Destroy_Tree(N : in out Node_Access) is
procedure free is new Ada.Unchecked_Deallocation(Node, Node_Access);
begin
if N.Left /= null then
Destroy_Tree(N.Left);
end if;
if N.Right /= null then
Destroy_Tree(N.Right);
end if;
Free(N);
end Destroy_Tree;
function Tree(Value : Integer; Left : Node_Access; Right : Node_Access) return Node_Access is
Temp : Node_Access := new Node;
begin
Temp.Data := Value;
Temp.Left := Left;
Temp.Right := Right;
return Temp;
end Tree;
procedure Preorder(N : Node_Access) is
begin
Put(Integer'Image(N.Data));
if N.Left /= null then
Preorder(N.Left);
end if;
if N.Right /= null then
Preorder(N.Right);
end if;
end Preorder;
procedure Inorder(N : Node_Access) is
begin
if N.Left /= null then
Inorder(N.Left);
end if;
Put(Integer'Image(N.Data));
if N.Right /= null then
Inorder(N.Right);
end if;
end Inorder;
procedure Postorder(N : Node_Access) is
begin
if N.Left /= null then
Postorder(N.Left);
end if;
if N.Right /= null then
Postorder(N.Right);
end if;
Put(Integer'Image(N.Data));
end Postorder;
procedure Levelorder(N : Node_Access) is
package Queues is new Ada.Containers.Doubly_Linked_Lists(Node_Access);
use Queues;
Node_Queue : List;
Next : Node_Access;
begin
Node_Queue.Append(N);
while not Is_Empty(Node_Queue) loop
Next := First_Element(Node_Queue);
Delete_First(Node_Queue);
Put(Integer'Image(Next.Data));
if Next.Left /= null then
Node_Queue.Append(Next.Left);
end if;
if Next.Right /= null then
Node_Queue.Append(Next.Right);
end if;
end loop;
end Levelorder;
N : Node_Access;
begin
N := Tree(1,
Tree(2,
Tree(4,
Tree(7, null, null),
null),
Tree(5, null, null)),
Tree(3,
Tree(6,
Tree(8, null, null),
Tree(9, null, null)),
null));
Put("preorder: ");
Preorder(N);
New_Line;
Put("inorder: ");
Inorder(N);
New_Line;
Put("postorder: ");
Postorder(N);
New_Line;
Put("level order: ");
Levelorder(N);
New_Line;
Destroy_Tree(N);
end Tree_traversal;
Parallel Code Solution
This part we implement a parallel algorithm with the same definition of traversal. First, we difine a function NEXT[x].The function NEXT[ x,], defining the successor of a field x, (of node x) in the Euler tour, is given as
Note that this NEXT function does not provide the successor of the last field of the root-node r in the tour. This is because we break the tour into a linked list such that u, is the starting field and r is the terminal field, where m = no-of-chiidren[r] + 1. The proposed linked list structure can be represented as an array [I . 2n - l] of SNODEREC:

To obtain the required tree-traversals, the following rules are operated on the linked list produced by algorithm GEN-COMP-NEXT:
pre-order traversal: select the first copy of each node;
post-order traversal: select the last copy of each node;
in-order traversal: delete the first copy of each node if it is not a leaf and delete the last copy of each node if it has more than one child.
Hash Tables
Hash Table Intro
Hash tables[3] are very efficient data structures often used in searching algorithms for fast lookup operations. Hash tables contain a series of "buckets" that function like indexes into an array, each of which can be accessed directly using their key value. The bucket for which a piece of data will be placed is determine by a special hashing function.
The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value.
In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list.[6]
Serial Code Example
Insert Example: Create new node if hash bucket doesnt exist, else append to the chain.
/**
* Put a key/value pair into the table by hashing the key to get the array
* index of the chain that should hold the node containing the pair.
* If an existing node with the same key is present then overwrite its value,
* otherwise add a new node.
*
*@param key key object reference
*@param val data object reference
*/
public void put(Object key, Object val)
{
int index = getIndex(key);
Node node = find(key, data[index]);
// Use helper method to determine if node with same key is already in
// chain. If not, add a new node to head of chain.
if (node == null)
{
data[index] = new Node(data[index], key, val);
}
else
{
// Otherwise update data value of existing node.
node.val = val;
}
}
Delete Example: Delete a node from the chain.
/**
* Remove a key/value pair from table if present, otherwise make no change.
*
*@param key key object reference
*/
public void remove(Object key)
{
int index = getIndex(key);
Node ref = data[index];
Node previous = null;
while (ref != null)
{
if ((ref.key).equals(key))
{
if (previous == null)
{
data[index] = ref.next;
}
else
{
previous.next = ref.next;
}
return;
}
previous = ref;
ref = ref.next;
}
}
Hash Function Example: Determines the proper hash table bucket.
/**
* Given a key, use a hash function to obtain the array index of the chain
* corresponding to the key.
* The hashCode method inherited (and possibly overridden)
* from class Object is called to do the hashing, with the returned
* value constrained to the hash table array bounds.
* The distribution of objects in the hash table will depend
* on the quality of the hash function implemented by hashCode.
*
*@param key reference to object to be hashed
*@return array index of chain corresponding to key
*/
private int getIndex(Object key)
{
return Math.abs(key.hashCode() % data.length);
}
Search Example: Find the proper node in the chain.
/**
* Find node given a key and a chain to search.
*
*@param key key object reference
*@param ref node object reference where search will start
*@return node object holding key or null if not found
*/
private Node find(Object key, Node ref)
{
while (ref != null)
{
if ((ref.key).equals(key))
{
return ref;
}
ref = ref.next;
}
return null;
}
Parallel Code Solution
The key issue in a hash table in a parallel environment is to make sure any update/insert/delete sequences have been completed properly prior to attempting subsequent operations to make sure the data has been synched appropriately. However, since access speed is such a critical component of the design of a hash table, it is essential to try and avoid using too many locks for performing synchronization. Fortunately, a number of lock-free hash designs have been implemented to avoid this bottleneck.
One such example in Java is the ConcurrentHashMap[9], which acts as a synchronized version of the HashMap. With this structure, there is full concurrency of retrievals and adjustable expected concurrency for updates. There is, however, no locking in this data structure and retrievals will typically run in parallel along with updates/deletes. Retrievals, however, will receive all most recently completed transactions even if it cannot get the values that haven't finished being updated. This both allows for efficiency and greater concurrency.
Search:
Retrieval operations proceed by first finding the head pointer for the desired bucket (which is done without locking, so it could be stale), and traversing the bucket chain without acquiring the lock for that bucket. If it doesn't find the value it is looking for, it synchronizes and tries to find the entry again[8]
/**
* This version of the get operation solves our concurrency issue by:
* 1) Try to search the head bucket without locking if possible to avoid the lock.
* 2) Only if it doesn't succeed, try to synchronize and search again.
*
*/
public Object get(Object key) {
int hash = hash(key); // throws null pointer exception if key is null
// Try first without locking...
Entry[] tab = table;
int index = hash & (tab.length - 1);
Entry first = tab[index];
Entry e;
for (e = first; e != null; e = e.next) {
if (e.hash == hash && eq(key, e.key)) {
Object value = e.value;
// null values means that the element has been removed
if (value != null)
return value;
else
break;
}
}
// Recheck under synch if key apparently not there or interference
Segment seg = segments[hash & SEGMENT_MASK];
synchronized(seg) {
tab = table;
index = hash & (tab.length - 1);
Entry newFirst = tab[index];
if (e != null || first != newFirst) {
for (e = newFirst; e != null; e = e.next) {
if (e.hash == hash && eq(key, e.key))
return e.value;
}
}
return null;
}
}
Removal:
Because a thread could see stale values for the link pointers in a hash chain, simply removing an element from the chain would not be sufficient to ensure that other threads will not continue to see the removed value when performing a lookup. Instead, as Listing 3 illustrates, removal is a two-step process -- first the appropriate Entry object is found and its value field is set to null, and then the portion of the chain from the head to the removed element is cloned and joined to the remainder of the chain following the removed element. Since the value field is volatile, if another thread is traversing the stale chain looking for the removed element, it will see the null value field immediately, and know to retry the retrieval with synchronization. Eventually, the initial part of the hash chain ending in the removed element will be garbage collected[8].
protected Object remove(Object key, Object value) {
/*
Find the entry, then
1. Set value field to null, to force get() to retry
2. Rebuild the list without this entry.
All entries following removed node can stay in list, but
all preceding ones need to be cloned. Traversals rely
on this strategy to ensure that elements will not be
repeated during iteration.
*/
int hash = hash(key);
Segment seg = segments[hash & SEGMENT_MASK];
synchronized(seg) {
Entry[] tab = table;
int index = hash & (tab.length-1);
Entry first = tab[index];
Entry e = first;
for (;;) {
if (e == null)
return null;
if (e.hash == hash && eq(key, e.key))
break;
e = e.next;
}
Object oldValue = e.value;
if (value != null && !value.equals(oldValue))
return null;
e.value = null;
Entry head = e.next;
for (Entry p = first; p != e; p = p.next)
head = new Entry(p.hash, p.key, p.value, head);
tab[index] = head;
seg.count--;
return oldValue;
}
}
Graphs
Graph Intro
A graph data structure is another type of linked-list structure that focuses on data that requires linking according to various types of relationships. For example, in a networking application, one network node may have connections to a variety of other network nodes. These nodes then also link to a variety of other nodes in the network. Using this connection of nodes, it would be possible to then find a path from one specific node to another in the chain. This could be accomplished by having each node contain a linked list of pointers to all other reachable nodes.
Serial Code Example
The following code snippet[5] gives some basic operations used in implementing a graph algorithm. Typically, you would need to do such operations as adding an edge to a node in the graph. The second function creates a shortest path algorithm from a given node to another desired node in the shortest number of hops possible.
/**
* Add a new edge to the graph.
*/
public void addEdge( String sourceName, String destName, double cost )
{
Vertex v = getVertex( sourceName );
Vertex w = getVertex( destName );
v.adj.add( new Edge( w, cost ) );
}
/**
* Single-source unweighted shortest-path algorithm.
*/
public void unweighted( String startName )
{
clearAll( );
Vertex start = (Vertex) vertexMap.get( startName );
if( start == null )
throw new NoSuchElementException( "Start vertex not found" );
LinkedList q = new LinkedList( );
q.addLast( start ); start.dist = 0;
while( !q.isEmpty( ) )
{
Vertex v = (Vertex) q.removeFirst( );
for( Iterator itr = v.adj.iterator( ); itr.hasNext( ); )
{
Edge e = (Edge) itr.next( );
Vertex w = e.dest;
if( w.dist == INFINITY )
{
w.dist = v.dist + 1;
w.prev = v;
q.addLast( w );
}
}
}
}
Parallel Code Solution
In an example of a possible parallel solution[10] to findest the shortest path, I have included the pseudocode listed below. In this case, the path algorithm itself can be parallelized for faster processing. In doing so, this pseudocode checks for any nodes marked previously deleted so that it will not include these nodes in subsequent executions of the path search.
Graph g = . . . // Undirected graph with integer edge weight s.
mstWeight = 0
Worklist wl = nodes of g
while (wl is not empty ) // In parallel.
a = remove arbitrary node from wl
if g does not contain a // Removed previously.
continue to next iteration
lt = null // Neighbor connected by lightest edge.
minWeight = infinity
for each edge(a, b)
wt = weight of edge(a, b)
if (wt < minWeight)
lt = b
minWeight = wt
contract edge (a , lt) // Removes lt from the graph.
mstWeight = mstWeight + minWeight
add node a to wl
return mstWeight
Quiz
1. Identify some issues with synchronizing insert/delete operations with linked list structures.
2. Identify some issues with synchronizing insert/search operations with linked list structures.
3. Which concurrency issues are of the most concern in a tree data structure?
4. What is the alternative to using a copy-scan technique in pointer-based programming?
5. Which concurrency issues are of the most concern with hash table data structures?
6. Which concurrency issues are of the most concern with graph data structures?
7. Why would you not want locking mechanisms in hash tables?
8. What is the nature of the linked list in a tree structure?
9. Describe a parallel alternative in the tree data structure.
10. Describe a parallel alternative in a graph data structure.
References
- http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html
- http://oreilly.com/catalog/masteralgoc/chapter/ch08.pdf
- http://www.devjavasoft.org/code/classhashtable.html
- http://osr600doc.sco.com/en/SDK_c++/_Intro_graph.html
- web.eecs.utk.edu/~berry/cs302s02/src/code/Chap14/Graph.java
- http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg
- http://rosettacode.org/wiki/Talk:Tree_traversal
- http://www.ibm.com/developerworks/java/library/j-jtp08223/
- http://docs.oracle.com/javase/1.5.0/docs/api/java/util/concurrent/ConcurrentHashMap.html
- http://users.ices.utexas.edu/~roman/cpc12.pdf