CSC/ECE 506 Spring 2012/4b rs

The limits to speedup

Introduction

In parallel computing, speedup refers to how much a parallel algorithm is faster than a corresponding sequential algorithm. According to Amdahl's law the speedup of a program using multiple processors in parallel computing is limited by the time needed for the sequential fraction of the program. But this solves a fixed problem in the shortest possible period of time, rather than solving the largest possible problem (e.g., the most accurate possible approximation) in a fixed "reasonable" amount of time. To overcome these shortcomings, John L. Gustafson and his colleague Edwin H. Barsis described Gustafson's Law, which provides a counterpoint to Amdahl's law, which describes a limit on the speed-up that parallelization can provide, given a fixed data set size.

Types of speedup

Scaled speedup

Scaled speedup is the speedup that can be achieved by increasing the data size. This increase in data size is done to solve a given problem on multiple parallel processors. In other words, with larger number of parallel processors at our disposal, we can increase the data size of the same problem and achieve higher speedup. This is what is referred to as scaled speedup. Means of achieving this speedup are exploited by Gustafson's Law.

Gustafson's Law

Gustafson's Law says that it is possible to parallelize computations when they involve significantly large data sets. It says that there is skepticism regarding the viability of massive parallelism. This skepticism is largely due to Amdahl's law, which says that the maximum speedup that can be achieved in a given problem with serial fraction of work s, is 1/s, even when the number of processors increases to an infinite number. For example, if 5% of computation in a problem is serial, then the maximum achievable speedup is 20 regardless of the number of processors. This is not a very encouraging result.

Figure 1. Gustafson's Law

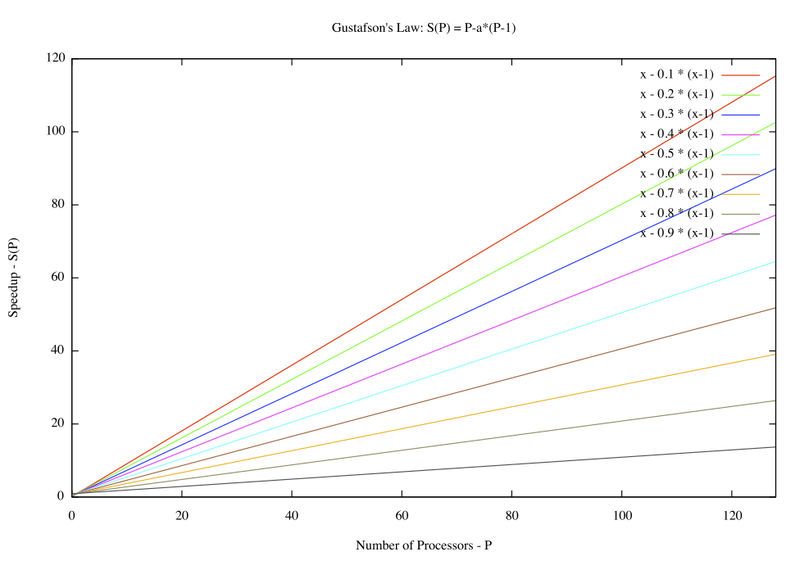
Amdahl's law does not fully exploit the computing power that becomes available as the number of machines increases. Gustafson's law addresses this limitation. It considers the effect of increasing the problem size. Gustafson reasoned that when a problem is ported onto a multiprocessor system, it is possible to consider larger problem sizes. In other words, the same problem with a larger number of data values takes the same time. The law proposes that programmers tend to set the size of problems to use the available equipment to solve problems within a practical fixed time. Larger problems can be solved in the same time if faster, i.e. more parallel equipment is available. Therfore, it should be possible to achieve high speedup if we scale the problem size.

Example:

   s (serial fraction of work) = 5%
   p (number of processors) = 20 
   speedup (Amdahl's Law) = 10.26
   scaled speedup (Gustafson's Law) = 19.05

Derivation of Gustafson's Law

If p is the number of processors, s is the amount of time spent (by a serial processor) on serial parts of a program and 1-s is the amount of time spent (by a serial processor) on parts of the program that can be done in parallel, then Amdahl's law says that speedup is given by:

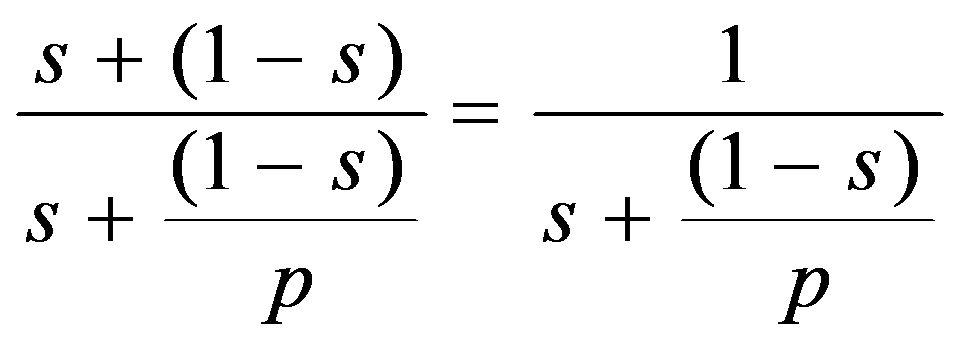
Let us consider a bigger problem size of measure n.

The execution of the program on a parallel computer is decomposed into:

where a is the sequential fraction, 1-s is the parallel fraction, ignoring overhead for now, and p is the number of processors working in parallel during the parallel stage.

The relative time for sequential processing would be s + p (1 - s), where p is the number of processors in the parallel case.

Speedup is therefore:

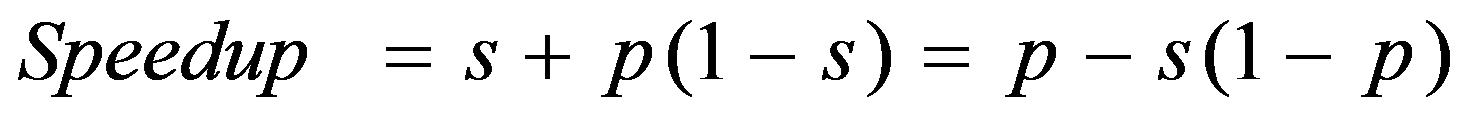
where s: = s(n) is the sequential fraction.

Assuming the sequential fraction s(n) diminishes with problem size n, then speedup approaches p as n approaches infinity, as desired. Thus Gustafson's law seems to rescue parallel processing from Amdahl's law.

Amdahl's law argues that even using massively parallel computer systems cannot influence the sequential part of a fixed workload. Since this part is irreducible, the sequential fraction of the fixed workload is a function of p that approaches 1 for large p. In comparison to that, Gustafson's law is based on the idea that the importance of the sequential part diminishes with a growing workload; and if n is allowed to grow along with p, the sequential fraction will not ultimately dominate.

In contrast with Amdahl's Law, this function is simply a line, and one with much more moderate slope: 1 – p.

It is thus much easier to achieve efficient parallel performance than is implied by Amdahl’s paradigm. The two approaches, fixed-sized and scaled-sized, are contrasted and summarized in Figure 2a and b.

Figure 2a. Fixed-Size Model: Speedup = 1 / (s + (1-s) / p)

Figure 2b. Scaled-Size Model: Speedup = s + p (1-s)

.

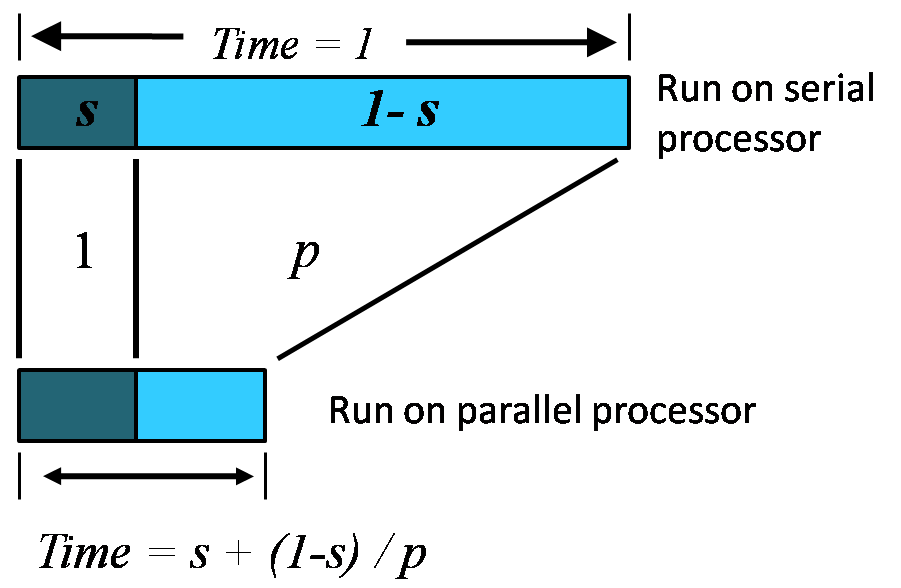
A Driving Metaphor

Amdahl's Law approximately suggests:

Suppose a car is traveling between two cities 60 miles apart, and has already spent one hour traveling half the distance at 30 mph. No matter how fast you drive the last half, it is impossible to achieve 90 mph average before reaching the second city. Since it has already taken you 1 hour and you only have a distance of 60 miles total; going infinitely fast you would only achieve 60 mph.

Gustafson's Law approximately states:

Suppose a car has already been traveling for some time at less than 90mph. Given enough time and distance to travel, the car's average speed can always eventually reach 90mph, no matter how long or how slowly it has already traveled. For example, if the car spent one hour at 30 mph, it could achieve this by driving at 120 mph for two additional hours, or at 150 mph for an hour, and so on.