CSC/ECE 506 Spring 2012/2a va

SAS programming on distributed-memory machines

Introduction

Decades ago, shared memory programming model was always implemented on shared memory hardware, while message-passing programming model was adopted on distributed memory hardware. However, nowadays the boundary has been broken. With the support of a shared virtual memory layer, we can program in shared memory fashion on distributed memory hardware. This article discusses how the shared-memory programming model is implemented on distributed-memory hardware.

Definitions

SAS Programming - Shared Address Space Programming, also referred to as the Shared Memory Model, is a style of parallel programming in which all the processors in the system have read and write access to the same memory. Information private to a single processor can be written to a designated memory location, but anything that is to be shared should be written to the shared location.<ref>http://www-public.int-evry.fr/~gibson/Teaching/CSC5021/ReadingMaterial/DagumMenon98.pdf</ref>

Distributed-Memory Machine - In the Distributed Memory Model, each processor has access only to its own memory. Information is shared between processors through a message passing system.<ref>http://www.cparity.com/projects/AcmClassification/samples/201065.pdf</ref>

Overview of Parallel Processing

Two Memory Models

In order to be effective, parallel processing must be supported on both a software level and a hardware level, with the appropriate systems in between. Two different memory models have been developed which handle parallel processing in distinct ways.

Shared-memory

This model is widely considered to be the most straightforward to program for. The main shortcoming of this model, however, is that it does not scale well due to the fact that the processors must share a common bus which serializes a significant portion of communication.

Distributed-memory

This model has the opposite strengths and weaknesses of the shared-memory model. It scales well as long as the machines are on a highspeed network, but the message-passing model associated with distributed-memory systems is much more difficult to program for.

Hybrid Model

SAS programming on distributed-memory machines is an attempt to give us the best of both the shared-memory model and the distributed memory model. Frequently referred to as the distributed shared-memory model or DSM, it uses a virtual address space or similar abstraction which gives the impression that the memory is shared even though it isn’t<ref>http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.17.7084&rep=rep1&type=pdf</ref>

Efficiency

DSMs are less efficient than a straight message passing system. The reason for this is that under the message passing model, the programmer is aware of when messages need to be passed and can program for those situations. With the DSM model, the programmer programs as if no messages need to be shared, but the DSM system must handle and attempt to anticipate when messages will need to be sent without knowing what applications will be running on it or how those applications have been programmed. <ref>http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.52.4066&rep=rep1&type=pdf</ref>

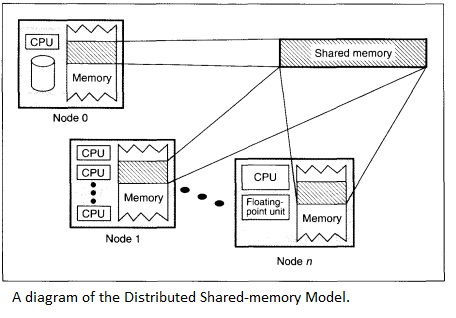
Accessing Remote Data

In the DSM, the system has to do a lookup for each reference to figure out if the data is local. If it’s not, a protocol action is invoked to acquire the data locally. This is referred to as access control.<ref>http://ftp.cs.wisc.edu/pub/techreports/1994/TR1238.pdf</ref> This is implemented in a variety of ways, including both hardware and software only solutions, as well solutions that include both hardware and software elements. All of these efforts are made in an attempt to bring the efficiency of the DSM model closer to that of a well-programmed message passing model. The efficiency issue with DSM boils down to how remote data is both stored and retrieved. There have been several different approaches to this problem

Static Data

Simply making the location of data within the overall system static solves the problem of how to find the data. This approach, however, creates a new problem of making sure that the data is properly distributed throughout the system. If all of the data ends up on a single node, this will create problems as multiple processes try to access the same data.

Dynamic Data

All other approaches to accessing remote data assume that data will move throughout the system as needed, and thus involve some way of keeping track of this data.

Centralized Server

This approach greatly simplifies the task of finding remote by having a single server keeping track of data as it moves around the system. The problem with this approach is that it serializes the task of finding remote memory locations, which all but defeats the purpose of having a parallel system in the first place.

Broadcasting

The broadcasting approach is for the node needing the data to send a message out to all the nodes in the system in order to find the one with the data. The problem with this approach is that it creates a lot of overhead as every node has to process the broadcast.

Owner based distribution

This system keeps track of the original owner of each piece of data. A node which needs the data then queries the original owner of the data, which passes the request off to the new owner if it has moved. This can result in excessive forwarding.<ref>http://www.cdf.toronto.edu/~csc469h/fall/handouts/nitzberg91.pdf</ref>

Transfer

This class of DSM machines is undoubtedly the fastest growing part in the family of high-performance computers. Although this DSM of machines is more difficult to deal with than shared-memory machines and DM-SIMD machines, the advantages of DSM-MIMD systems are clear: the bandwidth problem that haunts shared-memory systems is avoided because the bandwidth scales up automatically with the number of processors. Furthermore, the speed of the memory which is another critical issue with shared-memory systems (to get a peak performance that is comparable to that of DSM-MIMD systems, the processors of the shared-memory machines should be very fast and the speed of the memory should match it) is less important for the DSM-MIMD machines, because more processors can be configured without the afore mentioned bandwidth problems. <ref>http://www.netlib.org/utk/papers/advanced-computers/dm-mimd.html</ref>

Because a distributed-memory system is often called a multicomputer, it consists of multiple independent processing nodes with local memory modules, connected by a general interconnection network. The choice of the block size depends on some factors, the cost of communication: 1 byte message v.s. 1024 byte message; and locality of reference in the application. Most DSM systems use a page-based granularity with 1K byte to 8K byte. Larger page size, better locality of reference <ref>http://sslab.cs.nthu.edu.tw/~jimmy/present_2004/02_26/Introduction%20to%20Software%20Distributed%20Shared%20Memory%20Systems.ppt</ref>

Throughput

According to throughput requirements for SAS applications, it’s always best to use measured I/O throughput statistics from the application when building out the data architecture. However, when there are no real numbers the following can be used as general estimates for calculating throughput requirements for SAS:

Ad hoc SAS Power Users (heavy) 50-75 MB per second simultaneous process SAS Enterprise Guide / Microsoft Add-In (medium) 15 MB per second simultaneous user Business intelligence users (light) 1 MB per second simultaneous user

However, when testing throughput outside of SAS implementations, or when building an environment or the final distributed architecture, it is critical to test the I/O throughput capability before installing or testing the SAS implementation. Getting a baseline of the hardware before executing the SAS application will help isolate performance issues after a deploy of an application. If the baseline is not what was expected of the system, then this allows tuning and fixing the architecture before implementing SAS. Doing I/O tests early saves time and frustration in the deployment phase. <ref>http://support.sas.com/rnd/scalability/grid/Shared_FileSystem_GRID.pdf</ref>

Algorithm

Many SAS implemented system character functions are available to support unique, simple, and keyless data encryption algorithms. The cryptographic ciphers presented for SAS character date are based on the monoalphabetic, polyalphabetic, and transposition approach. The many SAS system functions inherit in Base SAS software make it possible to develop such algorithms. The data encryption algorithms presented uses many Base SAS system character functions. Here is a brief overview of each function: <ref>http://support.sas.com/techsup/technote/ts741.pdf</ref>

COLLATE Generates a collating sequence string , LEFT Removes leading spaces and shifts text to the left margin , LENGTH Returns a numeric value of a text string , REVERSE Swaps the order of a character expression , SCAN Searches for words and gives the result specified in the input argument , SUBSTR Extracts a segment from a text string , TRANSLATE Substitute characters with other characters TRIM Removes trailing paces

The use of SAS macro language made the specification of necessary information for the program very easy. Also, SAS showed a very high performance when dealing with large number of variables (sometimes more than 15000) and very small number of observations (3 or 4) when compared with alternative algorithms in commercial and noncommercial statistical packages. <ref>http://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm#statug_mcmc_sect053.htm</ref>

The algorithm demonstrated below is a sampling algorithm that can help understand the structure. Fitting a logistic model with PROC MCMC is straightforward. It can be used by the following statements:


   proc mcmc data=inputdata nmc=100000 propcov=quanew seed=17
             outpost=mcmcout;
      ods select PostSummaries ess;
      parms beta0-beta6;
      prior beta: ~ normal(0,var=25);
      mu = beta0 + beta1*cell + beta2*smear +
            beta3*infil +  beta4*li + beta5*blast +  beta6*temp;
      p = cdf('normal', mu, 0, 1);
      model remiss ~ bern(p);
   run;

The expression mu is the regression mean, and the CDF function links mu to the probability of remission p in the binary likelihood.

References