CSC/ECE 506 Spring 2011/ch2 dm

From Expertiza_Wiki
Jump to navigation Jump to search

Supplement to Chapter 2: The Data Parallel Programming Model

Chapter 2 of Solihin (2008) covers the shared memory and message passing parallel programming models. However, it does not address the data parallel model (a model composed of a set of identical tasks which operate on different subsets of common data), another commonly recognized parallel programming model covered in other treatments like Foster (1995) and Culler (1999).

Introduction

The data parallel programming model first appeared in the eighties as a programming model for SIMD (Single Instruction, Multiple Data) parallel machines. It's defined as multiple processing elements performing an action simultaneously on different parts of a data set and exchanging information globally before processing more code synchronously. Although the shared memory and message passing models are often presented as competing models, the data parallel model addresses fundamentally different programming concerns and can be used in conjunction with either. The main distinction between the data parallel model and the other two models has to do with the outcome of the individual steps instead of the method of communication. The data parallel model was developed for scientific calculations and is generally associated with applications that involve a data set which is typically organized into a common structure, such as an array or matrix. Data parallel processing has been found to be effective in situations where the computations allow the processing to be divided spatially over memories by involving every element of a matrix in a uniform way.

In addition to the data parallel model, the task parallel model (a model composed of a set of differing tasks which operate on common data.) will also be introduced briefly in Appendix B as a point of contrast with the data-parallel model. Furthermore, we will discuss the role of the shared memory and message passing models in the history of parallel computing. The goal of this supplement is to provide a treatment of the data parallel model which complements Chapter 2 of Solihin (2008).

Examples with the Data Parallel Model, Shared Memory, and Message Passing

While the shared memory and message passing models focus on how parallel tasks access common data, the data parallel model focuses on how to divide up work into parallel tasks. Data parallel algorithms exploit parallelism by dividing a problem into a number of identical tasks which execute on different subsets of common data.

Preliminary Example

A supporting example of a data parallel code can be seen in Code 2.5 from Solihin (2008). Shown below, it has been annotated with comments identifying the region of the code which is data parallel. 

// Data parallel code, adapted from Solihin (2008), p. 27.

id = getmyid(); // Assume id = 0 for thread 0, id = 1 for thread 1
local_iter = 4;
start_iter = id * local_iter;
end_iter = start_iter + local_iter;

if (id == 0)
    send_msg(P1, b[4..7], c[4..7]);
else
    recv_msg(P0, b[4..7], c[4..7]);

// Begin data parallel section

for (i = start_iter; i < end_iter; i++)
    a[i] = b[i] + c[i];
local_sum = 0;
for (i = start_iter; i < end_iter; i++)
    if (a[i] > 0)
        local_sum = local_sum + a[i];

// End data parallel section

if (id == 0)
{
    recv_msg(P1, &local_sum1);
    sum = local_sum + local_sum1;
    Print sum;
}
else
    send_msg(P0, local_sum);

In the code above, the three 8 element arrays are each divided into two 4 element chunks. In the data parallel section, the code executed by the two threads is identical, but each thread operates on a different chunk of data.

Main Example

Our main example is as follows. Suppose we want to perform the following task on an array a: updating each element of a by the product of itself and its index, and adding together the elements of a into the variable sum. The corresponding code is shown below. 

// simple sequential task
sum = 0;
for (i = 0; i < a.length; i++)
{
   a[i] = a[i] * i;
   sum = sum + a[i];
}

When we orchestrate the task using the data parallel programming model, the program can be divided into two parts. The first part performs the same operations on separate elements of the array for each processing element (sometimes referred to as PE). The second part reorganizes data among all processing elements (In our example data reorganization is summing up values across different processing elements).

First Part

The data parallel programming model defines the overall effects of parallel steps for the first part. Hillis (1986) points out that a major benefit of data parallel algorithms is that they easily scale to take advantage of additional processing elements simply by dividing the data into smaller chunks. Haveraaen (2000) also notes that data parallel codes typically bear a strong resemblance to sequential codes, making them easier to read and write.

The three code fragments below are examples for the first part of the program, shared-memory version of the second part, and message passing for the second part, respectively. 

// data parallel programming: let each PE perform the same task on different pieces of distributed data
pe_id = getid();
my_sum = 0;
for (i = pe_id; i < a.length; i += number_of_pe)         //separate elements of the array are assigned to each PE 
{
   a[i] = a[i] * i;
   my_sum = my_sum + a[i];                               //all PEs accumulate elements assigned to them into local variable my_sum
}

In the above code, data parallelism is achieved by letting each processing element perform actions on array's separate elements, which are identified using the PE's id. For instance, if three processing elements are used then one processing element would start at i = 0, one would start at i = 1, and the last would start at i = 2. Since there are three processing elements, the index of the array for each will increase by three on each iteration until the task is complete (note that in our example elements assigned to each PE are interleaved instead of continuous). If the length of the array is a multiple of three then each processing element takes the same amount of time to execute its portion of the task.

The picture below illustrates how elements of the array are assigned among different PEs for the specific case: length of the array is 7 and there are 3 PEs available. Elements in the array are marked by their indexes (0 to 6). As shown in the picture, PE0 will work on elements with index 0, 3, 6; PE1 is in charge of elements with index 1, 4; and elements with index 2, 5 are assigned to PE2. In this way, these 3 PEs work collectively on the array, while each PE works on different elements. Thus, data parallelism is achieved.

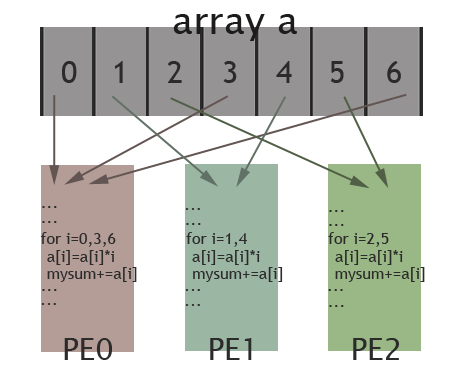
Illustration of data parallel programming(adapted from Introduction to Parallel Computing)

Second Part

The second part can be accomplished either through shared memory or message passing. The code below shows how data reorganization is done by the shared memory programming model. A shared variable is declared to store the global sum. Each PE accumulates their local my_sum into this variable. In this example, the lock() and unlock() routines are used to prevent race conditions and barrier ensures that all the local my_sum variables have been accumulated into the shared variable sum before the code proceeds. Notice that in this model there is only one copy of the data like in the data parallel model. However, in the shared memory model, the data must be protected since any PE could be using it at any point, whereas data is associated with a specific PE in the data parallel model. 

// data reorganization via shared memory
shared sum;
lock();                                                  //prevent race condition
sum = sum + my_sum;                                      //each PE adds up their local my_sum to shared variable sum 
unlock();
barrier;

The following section of code shows how data reorganization is done by the message passing programming model. PE0 acts as the one that collects the local my_sum variable from all the other PEs. This is done by the send_msg() and the recv_msg() routines: PEs other than PE0 send their my_sum variable as a message to PE0. PE0 receives the messages by specifying the sender in the for loop. PE ids are used in the message passing model in the same way they are in the data parallel model. On the contrary, in the data parallel model there is only one copy of data that is processed and there is no need to do any final accumulation by a single PE. 

// data reorganization via message passing
if (pe_id != 0) send_msg (0, my_sum);                    //PE other than PE0 send their local my_sum
else                                                     //PE0 does this
{
   for (i = 1; i < number_of_pe; i++)                    //for each other PE
   {
      recv_msg (i, temp);                                //receive local sum from other PEs
      my_sum = my_sum + temp;                            //accumulate into total
   }
   sum = my_sum;
}

History of Parallel Programming Models

Superscalar Machines

A superscalar processor is a pipelined processor able to retire multiple instructions in one cycle. The first superscalar machine was Cray's CDC 6600. It was released in 1964 and could execute 1 million floating point operations per second (1 MFLOP).

The CDC 6600 gained most of it's speed through delegating memory access and I/O to other processors, handling only arithmetic and logic. These peripheral processors, and the main CPU, could be designed to be as simple as possible. The CDC 6600 remained the world's fastest computer until 1969, being replaced by the CDC 7600.

Vector Machines

First appearing in the late 1960s, vector machines were able to apply a single instruction to multiple data values. This type of operation is used frequently in scientific fields or in multimedia.

The Solomon project at Westinghouse was one of the first machines to use vector operations. It's CPU had a large number of ALUs that would each be fed different data each cycle. Solomon was unsuccessful and was cancelled, eventually to be reborn as the ILLIAC IV at the University of Illinois. The ILLIAC IV showed great success at solving data-intensive problems, peaking at 150 MFLOPS under the right conditions.

An innovation came with the Cray-1 supercomputer in 1976. The innovation stemmed from the fact that the large data sets are often manipulated by several instructions back-to-back, such as an addition followed by a multiplication. The instruction pipeline of the Cray-1 was tweaked to take advantage of this. In the ILLIAC, up to 64 data points were loaded from memory with every instruction, but had to be stored back to manipulate the rest of the vector. The Cray computer was only able to load 12 data points, but by completing multiple instructions before continuing the total number of memory accesses decreased. In addition, the Cray-1 could perform at 240 MFLOPS. There continued to be new editions of Cray computers, theCray-2, Cray-3 etc. One of the most recent versions, Cray Y-MP, was sold from 1988 and used a MIMD architecture.

One of the later vector machines was the ETA10. It had shared memory 4M words and common memory 8M words, where each word was 64 bits. It was clocked at 24ns, but had a theorectical peak speed of 146 Mflops.

Many of these early machines were shared memory machines. This is likely because memory was very expensive and message passing requires multiple copies of data.

Connection Machines

The connection machine was a data parallel machine built in the 1980s. A connection machine had on the order of 64,000 processors. Each processor computed one bit of data and was connected to others via hyper-cube wiring. Tamiko Thiel describes the machine as being modeled after a human brain. The second connection machine (CM-2) which had more RAM and included floating point adders [1] came out in 1987, and two smaller editions, the CM-2a and the CM-200, were developed later.

Distributed Memory and Message Passing

In the 1980s, a manufacturing limit led to increased support for multiprocessor systems. The transputer architecture by Inmos was one of the first general-purpose microprocessors designed for parallel computing. The first transputers were released in 1984. Transputers were designed to be easily interlinkable; multiple processing chips could be easily combined into one system.

Each transputer processor could communicate with up to four other processors at up to 20 Mbps. Any number of processors could be combined into a massive processing farm. Of course, in large nets, the delay would be too great for any significant message passing.

Recent Data Parallel Computing

Today data parallelism is most commonly done in GPUs, due to the nature of graphics computation. Because GPUs often share memory with the main computer processor and other elements, they most commonly have a shared memory architecture. The supplement for chapter 2a discusses GPUs in depth.

Summary

Through the history of parallel computing we may observe the tradeoffs between the shared memory and message passing models. In the beginning, due to parallel programming being done for the most part exclusively on expensive and custom-made super computers, shared memory systems made sense. Later on, the invention of the personal computer and wider availability of smaller and less expensive computers led more people to a message passing approach. Most recently, data parallelism has been done with GPUs. Although shared-memory and message-passing models may be combined into hybrid approaches, the two models are fundamentally different ways of addressing the same problem (of access control to common data). In contrast, the data parallel model is concerned with a fundamentally different problem (how to divide work into parallel tasks). As such, the data parallel model may be used in conjunction with either the shared memory or the message passing model without conflict. In fact, Klaiber (1994) compares the performance of a number of data parallel programs implemented with both shared memory and message passing models.

One of the major advantages of combining the data parallel and message passing models is a reduction in the amount and complexity of communication required relative to a task parallel approach. Similarly, combining the data parallel and shared memory models tends to simplify and reduce the amount of synchronization required. If the task parallel code given in the appendix were modified from a message passing model to a shared memory model, the two threads would require 8 signals be sent between the threads (instead of 8 messages). In contrast, the data parallel code would require a single barrier before the local sums are added to compute the full sum.

Much as the shared memory model can benefit from specialized hardware, the data parallel programming model can as well. SIMD (single-instruction-multiple-data) processors are specifically designed to run data parallel algorithms. These processors perform a single instruction on many different data locations simultaneously. Modern examples include CUDA processors developed by nVidia and Cell processors developed by STI (Sony, Toshiba, and IBM). For the curious, example code for CUDA processors is provided in the Appendix. However, whereas the shared memory model can be a difficult and costly abstraction in the absence of hardware support, the data parallel model—like the message passing model—does not require hardware support.

Since data parallel code tends to simplify communication and synchronization, data parallel code may be easier to develop than a more task parallel approach. Once written, data parallel programs can scale easily to large numbers of processors. The data parallel model implicitly encourages data locality by having each thread work on a chunk of data, and the regular data chunks also make it easier to reason about where to locate data and how to organize it. On the other hand, it is possible that a problem may not decompose easily into subproblems relying on largely independent chunks of data. In this case, it may be impractical or impossible to apply the data parallel model.

The table below is extended from Table 2.1 on page 22 of the Solihin text. A column has been added for the data parallel model. The table compares some key characteristics of each programming model. As you can see, the complexity of the data parallel model comes mainly in the form of dividing up the work among PEs. Most of this work is done by the programmer and does not necessarily require special hardware, although, specific types of hardware can optimize the benefits of the model. For instance, SIMD and SPMD (single program, multiple data) hardware are examples that have efficiently utilized the data parallel model.


Aspects Data-Parallel Shared Memory Message Passing
Communication implicit - via loads/stores implicit - via loads/stores explicit messages
Synchronization none explicit implicit - via messages
Hardware support none typically required none
Development effort low low high
Tuning effort high high low

Definitions

  • Data parallel. A data parallel algorithm is composed of a set of identical tasks which operate on different subsets of common data.
  • Task parallel. A task parallel algorithm is composed of a set of differing tasks which operate on common data.
  • SIMD (single-instruction-multiple-data). A processor which executes a single instruction simultaneously on multiple data locations.

References

  • Barnes et al., The ILLIAC IV Computer
  • Björn Lisper, Data parallelism and functional programming, Lecture Notes in Computer Science, Volume 1132/1996, pp. 220-251, Springer Berlin, 1996.
  • David E. Culler, Jaswinder Pal Singh, and Anoop Gupta, Parallel Computer Architecture: A Hardware/Software Approach, Gulf Professional Publishing, August 1998.
  • Philip J. Hatcher, Michael Jay Quinn, Data-Parallel Programming on MIMD Computers, The MIT Press, 1991.
  • Yan Solihin, Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems, Solihin Books, August 2009.
  • Wikipedia, IBM Personal Computer [2]
  • Wikipedia, C.mmp [3]
  • Wikipedia, CDC 6600 [4]
  • Wikipedia, Computer Cluster [5]
  • Wikipedia, Cray-1 [6]
  • Wikipedia, Shared Memory Architecture [7]


Appendix A: Example of Data Parallel with Other Code

Comparison of the data parallel section of code identified above with the sequential Code 2.3 of Solihin (2008), which is reproduced below, supports the assertions of Hillis and Haveraaen mentioned above. The only differences between Codes 2.4 and 2.3 are the start and end indices and that, in the data parallel example, the variable sum is replaced by a private variable. Structurally the two codes are identical. 

// Sequential code, from Solihin (2008), p. 25.

for (i = 0; i < 8; i++)
    a[i] = b[i] + c[i];
sum = 0;
for (i = 0; i < 8; i++)
    if (a[i] > 0)
        sum = sum + a[i];
Print sum;

Appendix B: Data Parallel Versus Task-parallel

The logical opposite of data parallel is task parallel, in which a number of distinct tasks operate on common data. An example of a task parallel code which is functionally equivalent to the sequential and data parallel codes given above follows below for code 2.3 of Solihin (2008) which was above written in data parallel format. 

// Task parallel code.

int id = getmyid(); // assume id = 0 for thread 0, id = 1 for thread 1

if (id == 0)
{
    for (i = 0; i < 8; i++)
    {
        a[i] = b[i] + c[i];
        send_msg(P1, a[i]);
    }
}
else
{
    sum = 0;
    for (i = 0; i < 8; i++)
    {
        recv_msg(P0, a[i]);
        if (a[i] > 0)
            sum = sum + a[i];
    }
    Print sum;
}

In the code above, work is divided into two parallel tasks. The first performs the element-wise addition of arrays b and c and stores the result in a. The other sums the elements of a. These tasks both operate on all elements of a (rather than on separate chunks), and the code executed by each thread is different (rather than identical).

Since each parallel task is unique, a major limitation of task parallel algorithms is that the maximum degree of parallelism attainable is limited to the number of tasks that have been formulated. This is in contrast to data parallel algorithms, which can be scaled easily to take advantage of an arbitrary number of processing elements. In addition, unique tasks are likely to have significantly different run times, making it more challenging to balance load across processors. Haveraaen (2000) also notes that task parallel algorithms are inherently more complex, requiring a greater degree of communication and synchronization. In the task parallel code above, after thread 0 computes an element of a it must send it to thread 1. To support this, sends and receives occur every iteration of the two loops, resulting in a total of 8 messages being sent between the threads. In contrast, the data parallel code sends only 2 messages, one at the beginning and one at the end. The table below summarizes the key differences between data parallel and task parallel programming models.

Comparison between data parallel and task parallel programming models.
Aspects Data Parallel Task Parallel
Decomposition Partition data into subsets Partition program into subtasks
Parallel tasks Identical Unique
Degree of parallelism Scales easily Fixed
Load balancing Easier Harder
Communication overhead Lower Higher

One important feature of data parallel programming model or data parallelism (SIMD) is the single control flow: there is only one control processor that directs the activities of all the processing elements. In stark contrast to this is task parallelism (MIMD: Multiple Instruction, Multiple Data): characterized by its multiple control flows, it allows the concurrent execution of multiple instruction streams, each manipulates its own data and services separate functions. Below is a contrast between the data parallelism and task parallelism models from wikipedia: SIMD and MIMD. In the following subsections we continue to compare and contrast different features of data parallel model and task-parallel model to help reader understand the unique characteristics of data parallel programming model.

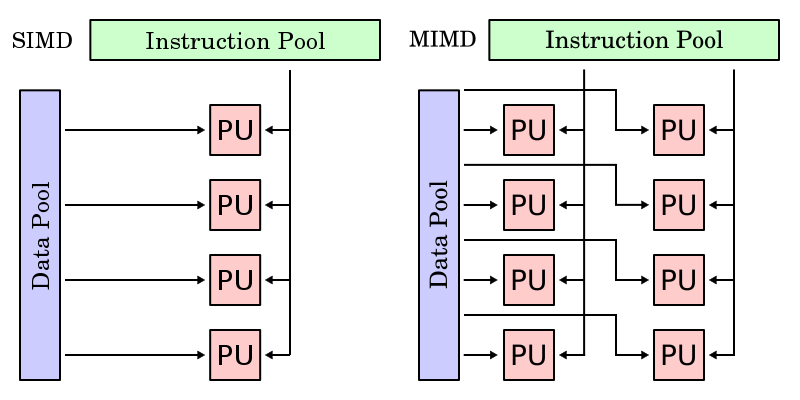
contrast between data parallelism and task parallelism

Synchronous vs Asynchronous

While the lockstep imposed by data parallelism on all data streams ensures synchronous computation (all PEs perform their tasks at the exact same pace), every processor in task parallelism performs its task at their own pace, which we call asynchronous computation. Thus, at a certain point of a task parallel program's execution, communication and synchronization primitives are needed to allow different instruction streams to coordinate their efforts, and that is where variable-sharing and message-passing come into play.

Determinism vs. Non-Determinism

Data parallelism's synchronous nature and task parallelism's asynchronism give rise to another pair of features that add to the difference between these two models: determinism versus non-determinism. Data parallelism is deterministic, i.e. computing with the same input will always yield the same result, since its synchronism ensures that issues like relative timing between PEs will not arise. In contrast, task parallelism's asynchronous updates of common data can give rise to non-determinism, i.e, the same input won't always yield the same computation result (the result of a computation will depend also on factors outside the program control, such as scheduling and timing of other PEs). Obviously, non-determinism makes it harder to write and maintain correct programs. This partially explains the advantage of data parallel programming model over data parallelism in terms of development effort (also discussed in section 4.2).

Appendix C: C for CUDA Example Code

The following code is a data parallel implementation of the sequential Code 2.3 from Solihin (2008) using C for CUDA. It is presented to give an impression of programming for a SIMD architecture, but a detailed discussion is beyond the scope of this supplement. Ignoring memory allocation issues, the code is very similar to the data parallel example, Code 2.5 from Solihin (2008), discussed earlier. The main difference is the presence of a control thread that sends the parallel tasks to the CUDA device. 

// Data parallel implementation of the example code using C for CUDA.

#include <iostream>

__global__ void kernel(float* a, float* b, float* c, float* local_sum)
{
    int id = threadIdx.x;
    int local_iter = 4;
    int start_iter = id * local_iter;
    int end_iter = start_iter + local_iter;

    // Begin data parallel section

    for (int i = start_iter; i < end_iter; i++)
        a[i] = b[i] + c[i];
    local_sum[id] = 0;
    for (int i = start_iter; i < end_iter; i++)
        if (a[i] > 0)
            local_sum[id] = local_sum[id] + a[i];

    // End data parallel section
}

int main()
{
    float h_a[8], h_b[8], h_c[8], h_sum[2];
    float *d_a, *d_b, *d_c, *d_sum;
    float sum;

    size_t size = 8 * sizeof(float);
    size_t size2 = 2 * sizeof(float);

    cudaMalloc((void**)&d_a, size);
    cudaMalloc((void**)&d_b, size);
    cudaMalloc((void**)&d_c, size);
    cudaMalloc((void**)&d_local_sum, size2);

    cudaMemcpy(d_b, h_b, size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_c, h_c, size, cudaMemcpyHostToDevice);

    kernel<<<1, 2>>>(d_a, d_b, d_c, d_sum);

    cudaMemcpy(h_a, d_a, size, cudaMemcpyDeviceToHost);
    cudaMemcpy(h_sum, d_sum, size2, cudaMemcpyDeviceToHost);

    sum = h_sum[0] + h_sum[1];
    std::cout << sum;

    cudaFree(d_a);
    cudaFree(d_b);
    cudaFree(d_c);
    cudaFree(d_sum);
}
Retrieved from "https://wiki.expertiza.ncsu.edu/index.php?title=CSC/ECE_506_Spring_2011/ch2_dm&oldid=44755"