CSC/ECE 506 Spring 2010/ch 3 yl

Supplement to Chapter 3: Support for parallel-programming models. Discuss how DOACROSS, DOPIPE, DOALL, etc. are implemented in packages such as Posix threads, Intel Thread Building Blocks, OpenMP 2.0 and 3.0.

Parallel-programming models

Loop-independent vs. Loop-carried dependences

Before performing the three kinds of parallelism analysis, we need to discuss about loop-dependence analysis first.

Statement dependences

To discuss code analysis, let's define the framework as follows. Let S denote a statement in the source code. Let [] denote loop iteration space. Let S1 -> S2 denote statement S1 executes before S2. Then, we further define three statement dependences:

• S1 ->T S2 denotes true dependence: S1 -> S2, and S1 writes to a location that is read by S2.
• S1 ->A S2 denotes anti dependence: S1 -> S2, and S1 reads a location written by S2.
• S1 ->O S2 denotes output dependence: S1 -> S2, and S1 writes to the same location written by S2.

To give a better understanding, we illustrate the dependences using the code section below:

for (i=1; i<N; i++)
    S1: a[i] = i;
    S2: b[i] = a[i-1];
    S3: b[i] = a[i]+c[i+1];
    S4: c[i] = 2*i;

The dependences corresponding to the code are:

• S1[i-1] ->T S2[i]: a[i-1] is written in statement S1 in the (i-1)th iteration, and read in S2 in the ith iteration.
• S1[i] ->T S3[i]: a[i] is written in statement S1 in the ith iteration, and read in S3 in the ith iteration.
• S3[i] ->A S4[i+1]: c[i] is read in statement S3 in the ith iteration, and written in S4 in the (i+1)th iteration.
• S2[i] ->O S3[i]: b[i] is written in statement S2 in the ithe iteration, and also written in S3 in the ith iteration.

Loop-independent dependences

Loop-independent dependence is defined as a dependence that exists between statements within a loop iteration. Use the example code section above again to illustrate this definition.

• S1[i] ->T S3[i]: loop-independent dependence. Because a[i] is written in S1 in the ith iteration, and read in S3 in the same iteration.
• S2[i] ->O S3[i]: loop-independent dependence. Because b[i] is written in statement S2 in the ithe iteration, and also written in S3 in the same iteration.

Loop-carried dependences

Loop-carried dependence is defined as a dependence that exists between a statement in one iteration with another statement in a different iteration. Use the example code section above again to illustrate this definition.

• S1[i-1] ->T S2[i]: loop-carried dependence. Because a[i-1] is written in statement S1 in the (i-1)th iteration, and read in S2 in the next iteration.
• S3[i] ->A S4[i+1]: loop-carried dependence. Because c[i] is read in statement S3 in the ith iteration, which will be written in S4 in the next iteration.

DOALL

DOALL is the simplest kind of data parallelism, and in some special cases, could be the most efficient parallelism. In this kind of parallelism, all the parallel loop iterations are independent of one another and each of them is an individual parallel task. Let's use the example 3.1 in Solihin's Textbook to illustrate the DOALL parallelism.

for (i=1; i<n; i++)
    for (j=1; j<n; j++)
       S2: a[i][j] = b[i][j] + c[i][j];
       S3: b[i][j] = a[i][j-1] + d[i][j];

In this example, for i loop is the parallel loop. We could see that there is no loop-carried dependence across i iteration, which means that all iterations in the for i loop are independent with any other i iterations. This fact makes all the i iterations an individual parallel task and could be executed by individual processors at the same time.

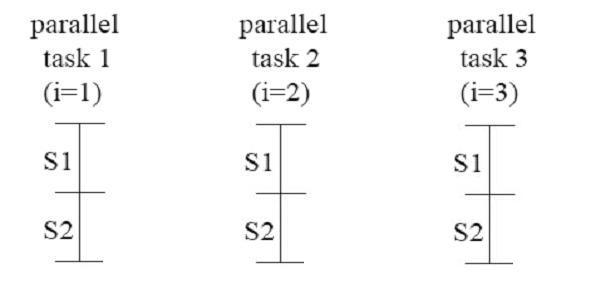
In order to illustrate the execution of DOALL and give a better view of how it really works, we prune the inner loop that messes up our vision. The following is the simpler example:

for (i=1; i<n; i++)
       S2: a[i] = b[i] + c[i];
       S3: b[i] = a[i] + d[i];

Again, there is no loop-carried dependence across iterations, and all iterations are independent with any other iterations. All the iterations could be executed simultaneously as parallel tasks. The figure of execution of the iterations is shown as below:

To show the speedup obtained through the DOALL parallelism, we denote T_S2, T_S3 as the execution time of statement S2, S3 respectively. If the loop is executed sequentially, the execution time is ( n - 1 ) ( T_S2 + T_S3 ). With the DOALL parallelism, the new execution time is just ( T_S2 + T_S3 ). The speedup ratio is ( n - 1 ), which is really good. However, the DOALL requires strict conditions. If there is any loop-carried dependences, it can not be adopted, where DOACROSS and DOPIPE should be considered.

DOACROSS

In code 3.7, apparently there is a loop-carried dependence existing in the code.

S[i] -> T S[i+1]

Obviously, there is no way to implement it as DOALL parallelism.

Code 3.7 A loop with loop-carried dependence
for (i=1; i<=N; i++) {
 S: a[i] = a[i-1] + b[i] * c[i];}

If we split code 3.7 as two loops, then the fist loop can be implement in DOALL parallism. In code 3.8, first of all, we create a new array named temp[i]. Second, we put temp[i] in a loop which is individual and loop-independence. However, this solution generated a disadvantage: high storage. Due to increasing the array size of temp[i] by i++, the size of temp depends on the number of iterations instead of threads. If N ( # of iteration) is bigger, then the size of temp will be larger.

Code 3.8 A split version of the loop in Code 3.7
for (i=1; i<=N; i++) {  //this loop has DOALL parallelism
  S1: temp[i] = b[i] * c[i];}  
for (i=1; i<=N; i++) {
  S2: a[i] = a[i-1] + temp[i];}

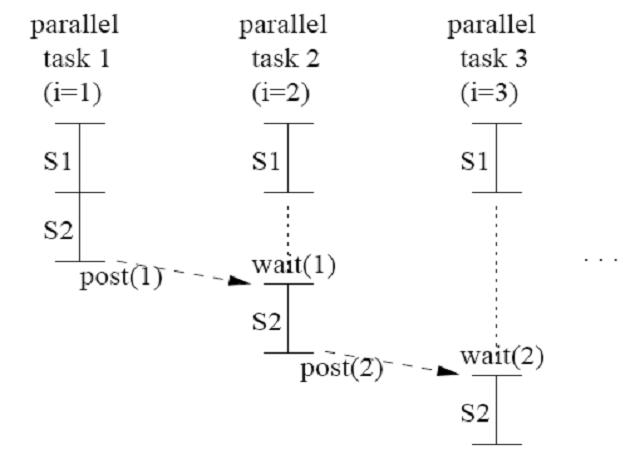
Let's see code 3.9, We still create a new array temp[i]. There are two differences between code 3.9 (DOACROSS) and code 3.8 (DOALL). First, the size of array is not increasing by the # of iterations but the # of threads, because temp[i] is not a shared array but a private scalar. Second, there is only one loop which contains S1 and S2. In DOACROSS parallelism, we insert two primitives, wait(name) and post(name). The principle of DOACROSS parallelism is to insert point-to-point synchronization. Notice the statement post(i) and and wait(i-1). post(i) is a signal produced by producer a[i]. Once a[i] has been produced, it will be post immediately. Meanwhile, the consumer is waiting i-1 by using wait(i-1). The reason makes consumer has to wait the previous a[i] is because S2 has to use a[i-1] to calculate to generate a[i]. Next, when S2 produce a[i], it will post it, post(i), to let the next consumer consume it. We will discuss how DOACROSS parallelism works in figure later.

Code 3.9 Exploiting DOACROSS parallelism in the loop from code 3.7
post(0);
for (i=1; i<=N; i++) {
  S1: temp[i] = b[i] * c[i];}
  wait(i-1);
  S2: a[i] = a[i-1] + temp[i];
  post(i);}

In this figure, we will introduce how DOACROSS parallelism executes by using post and wait. In task 1 (i=1), S2 post post(1) as it finishes its own statement. Next, in task 2 (i=2), when S1 finished its own statement, task 2 has to wait until task 1 finishes and post (1). The statement of S2 in task 2 is a[2] = a[2-1] + temp[2]; and it means S2 can not produce value without a[1]. The same to task 3, S2 in task 3 is a[3] = a[3-1] + temp[3]; and has to wait until task 2 finishes its task and post a[2].

DOPIPE

In code 3.12, there is a loop-carried dependence existing in the loop.

S1[i]-> T S1[i+1]

S1 is true dependence on S1[i+1], because S1[i] writes first, and then S1[i+1] reads.

Code 3.12 A loop amenable to pipelined parallelism
for (i=1; i<=N; i++) {
 S1: a[i] = a[i-1] + b[i];
 S2: c[i] = c[i] + a[i];}

Here we split code 3.12 in 2 loops and make it parallelized in DOALL parallelism. For the first loop, there is no way to use DOALL parallelism because of loop-carried dependence. Otherwise, for the second loop, it is available to use DOALL parallelism since there is no loop carried dependence but loop-independence. Howevr, DOALL is not the only solution to parallelize code 3.12 and it still has an disadvantage. If there are only a few processors to run this program, then the speedup will not be too much. We will introduce another solution, DOPIPE parallelism, in code 3.13.

Code DOALL parallelism(transformed from 3.12) 
for (i=1; i<=N; i++) {  
  S1: a[i] = a[i-1] + b[i];}
for (i=1; i<=N; i++) { //this loop has DOALL parallelism
  S2: c[i] = c[i] + a[i];}

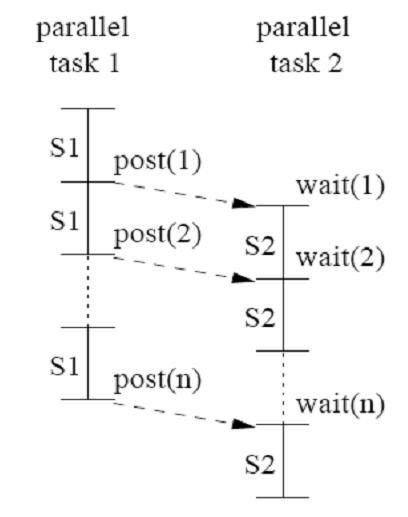
Here, we use DOPIPE parallelism to solve code 3.12. We still split code 3.12 as twp loops and insert primitive synchronization, post and wait. In order to calculate c[i], S2 has to get the value of a[i]. However, there is no a[i] in the second loop. S2 has to wait until S1 finished processing a[i] and post it. Once S1 produces a[i], S2 consumes a[i] immediately and starts process its own statement. We will explain this principle in figure later.

Code 3.13 DOPIPE parallel version of the loop from code 3.12
for (i=1; i<=N; i++) {  //this loop has DOALL parallelism
  S1: a[i] = a[i-1] + b[i];
  post(i);}
for (i=1; i<=N; i++) {
  wait(i);
  S2: c[i] = c[i] + a[i];}

This figure present us how DOPIPE parallelism works. Each task processes different statement. For example, task1 processes S1 and task2 processes S2 in this figure. On the other hands, S1 is a producer to produce a[i]. Once S1 produces a[i], it will post a[i], post(i), to let S2 consume. S2 has to wait for a[i] by using wait(i), because S2 does not know the value of a[i] until S1 produces and posts it.

Implementation

Intel Thread Building Blocks

Intel Threading Building Blocks (Intel TBB) is a library that supports scalable parallel programming using standard ISO C++ code. It does not require special languages or compilers. It is designed to promote scalable data parallel programming. The library consists of data structures and algorithms that allow a programmer to avoid some complications arising from the use of native threading packages such as POSIX threads, Windows threads, or the portable Boost Threads in which individual threads of execution are created, synchronized, and terminated manually. Instead the library abstracts access to the multiple processors by allowing the operations to be treated as "tasks," which are allocated to individual cores dynamically by the library's run-time engine, and by automating efficient use of the cache. This approach groups TBB in a family of solutions for parallel programming aiming to decouple the programming from the particulars of the underlying machine. Also, Intel Threading Building Blocks provides net results, which enables you to specify parallelism more conveniently than using raw threads, and at the same time can improve performance.

Variables Scope

Intel TBB is a collection of components for parallel programming, here is the overview of the library contents:

• Basic algorithms: parallel_for, parallel_reduce, parallel_scan
• Advanced algorithms: parallel_while, parallel_do,pipeline, parallel_sort
• Containers: concurrent_queue, concurrent_vector, concurrent_hash_map
• Scalable memory allocation: scalable_malloc, scalable_free, scalable_realloc, scalable_calloc, scalable_allocator, cache_aligned_allocator
• Mutual exclusion: mutex, spin_mutex, queuing_mutex, spin_rw_mutex, queuing_rw_mutex, recursive mutex
• Atomic operations: fetch_and_add, fetch_and_increment, fetch_and_decrement, compare_and_swap, fetch_and_store
• Timing: portable fine grained global time stamp
• Task Scheduler: direct access to control the creation and activation of tasks

Then we will focus on some specific TBB variables.

parallel_for

Parallel_for is the template function that performs parallel iteration over a range of values. In Intel TBB, a lot of DOALL cases could be implemented by using this function. The syntax is as follows:

template<typename Index, typename Function>
Function parallel_for(Index first, Index_type last, Index step, Function f);
template<typename Range, typename Body>
void parallel_for( const Range& range, const Body& body, [, partitioner] );

OpenMP

The OpenMP Application Program Interface (API) supports multi-platform shared-memory parallel programming in C/C++ and Fortran on all architectures, including Unix platforms and Windows NT platforms. Jointly defined by a group of major computer hardware and software vendors, OpenMP is a portable, scalable model that gives shared-memory parallel programmers a simple and flexible interface for developing parallel applications for platforms ranging from the desktop to the supercomputer.

OpenMP Clauses

There are many different types of clauses in OpenMP and each of them has various characteristics. Here we introduce data sharing attribute clauses, Synchronization clauses, Scheduling clauses, Initialization and Reduction.

Data sharing attribute clauses

• shared: the data within a parallel region is shared, which means visible and accessible by all threads simultaneously. By default, all variables in the work sharing region are shared except the loop iteration counter.

 Format: shared (list)

 SHARED variables behave as follows:
 1. Existing in only one memory location and all threads can read or write to that address 

• private: the data within a parallel region is private to each thread, which means each thread will have a local copy and use it as a temporary variable. A private variable is not initialized and the value is not maintained for use outside the parallel region. By default, the loop iteration counters in the OpenMP loop constructs are private.

 Format: private (list)

 PRIVATE variables behave as follows: 
   1. A new object of the same type is declared once for each thread in the team
   2. All references to the original object are replaced with references to the new object
   3. Variables declared PRIVATE should be assumed to be uninitialized for each thread 

• default: allows the programmer to state that the default data scoping within a parallel region will be either shared, or none for C/C++, or shared, firstprivate, private, or none for Fortran. The none option forces the programmer to declare each variable in the parallel region using the data sharing attribute clauses.

 Format: default (shared | none)

 DEFAULT variables behave as follows: 
   1. Specific variables can be exempted from the default using the PRIVATE, SHARED, FIRSTPRIVATE, LASTPRIVATE, and REDUCTION clauses. 
   2. Using NONE as a default requires that the programmer explicitly scope all variables. 

• firstprivate:like private except initialized to original value.

 Format: firstprivate (list)

 FIRSTPRIVATE variables behave as follows: 
   1. Listed variables are initialized according to the value of their original objects prior to entry into the parallel or work-sharing construct. 

• lastprivate: like private except original value is updated after construct.

 Format: lastprivate (list)

• reduction: a safe way of joining work from all threads after construct.

 Format: reduction (operator: list)

 REDUTION variables behave as follows: 
   1. Variables in the list must be named scalar variables. They can not be array or structure type variables. They must also be declared SHARED in the enclosing context.
   2. Reduction operations may not be associative for real numbers.

Synchronization clauses

• critical section: the enclosed code block will be executed by only one thread at a time, and not simultaneously executed by multiple threads. It is often used to protect shared data from race conditions.

 Format: #pragma omp critical [ name ]  newline
          structured_block

 CRITICAL SECTION behav as follows:
   1.f a thread is currently executing inside a CRITICAL region and another thread reaches that CRITICAL region and attempts to execute it, it will block until the first thread exits that CRITICAL region. 

• atomic: similar to critical section, but advise the compiler to use special hardware instructions for better performance. Compilers may choose to ignore this suggestion from users and use critical section instead.
• ordered: the structured block is executed in the order in which iterations would be executed in a sequential loop
• barrier: each thread waits until all of the other threads of a team have reached this point. A work-sharing construct has an implicit barrier synchronization at the end.
• nowait: specifies that threads completing assigned work can proceed without waiting for all threads in the team to finish. In the absence of this clause, threads encounter a barrier synchronization at the end of the work sharing construct.

Scheduling clauses

• schedule(type, chunk): This is useful if the work sharing construct is a do-loop or for-loop. The iteration(s) in the work sharing construct are assigned to threads according to the scheduling method defined by this clause. The three types of scheduling are:

1. static: Here, all the threads are allocated iterations before they execute the loop iterations. The iterations are divided among threads equally by default. However, specifying an integer for the parameter "chunk" will allocate "chunk" number of contiguous iterations to a particular thread.
2. dynamic: Here, some of the iterations are allocated to a smaller number of threads. Once a particular thread finishes its allocated iteration, it returns to get another one from the iterations that are left. The parameter "chunk" defines the number of contiguous iterations that are allocated to a thread at a time.
3. guided: A large chunk of contiguous iterations are allocated to each thread dynamically (as above). The chunk size decreases exponentially with each successive allocation to a minimum size specified in the parameter "chunk"

Initialization

• firstprivate: the data is private to each thread, but initialized using the value of the variable using the same name from the master thread.
• lastprivate: the data is private to each thread. The value of this private data will be copied to a global variable using the same name outside the parallel region if current iteration is the last iteration in the parallelized loop. A variable can be both firstprivate and lastprivate.
• threadprivate: The data is a global data, but it is private in each parallel region during the runtime. The difference between threadprivate and private is the global scope associated with threadprivate and the preserved value across parallel regions.

Reduction

• reduction(operator | intrinsic : list): the variable has a local copy in each thread, but the values of the local copies will be summarized (reduced) into a global shared variable. This is very useful if a particular operation (specified in "operator" for this particular clause) on a datatype that runs iteratively so that its value at a particular iteration depends on its value at a previous iteration. Basically, the steps that lead up to the operational increment are parallelized, but the threads gather up and wait before updating the datatype, then increments the datatype in order so as to avoid racing condition. This would be required in parallelizing Numerical Integration of functions and Differential Equations, as a common example.

DOALL

In code 3.20, first it must include the header file omp.h which contains OpenMP function clarations. Next, A paralel region is started by #pragma omp parallel and we enclose this program bu curly brackets. We can use (setenv OMP_NUM_THREADS n) to specify the number of threads. Another way to determine the number of threads is directly calling a function (omp_set_numtheads (n)). Code 3.20 only has one loop to execute and we want to execute in parallel, so we combine the start of the parallel loop and the start of the parallel region with one directive #pragma omp parallel for.

Code 3.20 A DOALL parallelism example in OpenMP
#include <omp.h>
...
#pragma omp parallel //start of parallel region
{
 ...
 #pragma omp parallel for default (shared)
 for ( i = 0; i < n ; i++)
   A[i] = A[i] + A[i] - 3.0;
}//end for parallel region

Apparently, there is no loop-carried dependence in i loop. With OpenMP, we only need to insert the pragma directive parallel for. The dafault(shared) clauses states that all variables within the scope of the loop are shared unless otherwise specified.

Functional Parallelism

In order to introduce function parallelism, we want to execute some code section in parallel with another code section. We use code 3.21 to show two loops execute in parallel with respect to one another, although each loop is sequentially executed.

Code 3.21 A function parallelism example in OpenMP
pragma omp parallel shared(A, B)private(i)
{
 #pragma omp sections nowait
 {
     pragma omp section
     for( i = 0; i < n ; i++)
        A[i] = A[i]*A[i] - 4.0;
     pragma omp section
     for( i = 0; i < n ; i++)
        B[i] = B[i]*B[i] - 9.0;
 }//end omp sections
}//end omp parallel

In code 3.21, there are two loops needed to be executed in parallel. We just need to insert two pragma omp section statements. Since we insert these two statements, those two loops will execute sequentially.

POSIX Threads

POSIX Threads, or Pthreads, is a POSIX standard for threads. The standard, POSIX.1c, Threads extensions (IEEE Std 1003.1c-1995), defines an API for creating and manipulating threads.

Contents

Pthreads defines a set of C programming language types, functions and constants. It is implemented with a pthread.h header and a thread library.

There are around 100 Pthreads procedures, all prefixed "pthread_" and they can be categorized into four groups:

• Thread management - creating, joining threads etc : pthread_create(); pthread_join()
• Mutexes - pthread_mutex_lock(); pthread_mutex_trylock(); pthread_mutex_unlock()
• Condition variables - pthread_cond_signal(); pthread_cond_broadcast(); pthread_cond_wait(); pthread_cond_timedwait();pthread_cond_reltimedwait_np()
• Synchronize between threads using read/write locks and barriers - pthread_rwlock_rdlock(); pthread_rwlock_tryrdlock(); pthread_rwlock_wrlock();pthread_rwlock_trywrlock(); pthread_rwlock_unlock();pthread_barrier_init(); pthread_barrier_wait()

DOALL example

The following is a simple code example in C, as DOALL parallelism, to print out each threads' ID#.

#include <pthread.h>
#include <stdio.h>
#include <stdlib.h>
#define NUM_THREADS     5
 
void *PrintHello(void *threadid)
{
   long tid;
 
   tid = (long)threadid;
   printf("Hello World! It's me, thread #%ld!\n", tid);
   pthread_exit(NULL);
}
 
int main (int argc, char *argv[])
{
   pthread_t threads[NUM_THREADS];
 
   int rc;
   long t;
   for(t=0; t<NUM_THREADS; t++){
      printf("In main: creating thread %ld\n", t);
      rc = pthread_create(&threads[t], NULL, PrintHello, (void *)t);
 
      if (rc){
         printf("ERROR; return code from pthread_create() is %d\n", rc);
         exit(-1);
      }
   }
   pthread_exit(NULL);
}

Comparison among the three

A unified example

We use a simple parallel example from Sourceforge.net to show how it will be implemented in the three packages, namely, POSIX Threads, Intel TBB, OpenMP, to show some common and differences among them.

Following is the original code:

Grid1 *g = new Grid1(0, n+1);
Grid1IteratorSub it(1, n, g);
DistArray x(g), y(g);
...
float e = 0;
ForEach(int i, it,
   x(i) += ( y(i+1) + y(i-1) )*.5;
   e += sqr( y(i) ); )
...

Then we are going to show the implementations in different packages, and also make a brief summary of the three packages.

In POSIX Thread

POSIX Thread: Symmetric multi processing, e.g. SMP multi-processor computers, multi-core processors, virtual shared memory computer.

Data layout: A single global memory. Each thread reads global shared data and writes to a private fraction of global data.

A simplified translation of the example parallel-for loop is given below.

Global declaration:

#include <pthread.h>
float *x, *y;
float vec[8];
int nn, pp;

thread code:

void *sub1(void *arg) {
   int p = (int)arg;
   float e_local = 0;
   for (int i=1+(nn*p)/pp; i<1+(nn*(p+1))/pp; ++i) {
     x[i] += ( y[i+1] + y[i-1] )*.5;
     e_local += y[i] * y[i];
   }
   vec[p] = e_local;
   return (void*) 0;
}

main code:

x = new float[n+1];
y = new float[n+1];
...
float e = 0;
int p_threads = 8;
nn = n-1;
pp = p_threads;
pthread_t threads[8];
pthread_attr_t attr;
pthread_attr_init(&attr);
for (int p=0; p<p_threads; ++p)
   pthread_create(&threads[p], &attr,
     sub1, (void *)p);
for (int p=0; p<p_threads; ++p) {
   pthread_join(threads[p], NULL);
   e += vec[p];
}
...
delete[] x, y;

In Intel Threading Building Blocks

Intel TBB: A C++ library for thread programming, e.g. SMP multi-processor computers, multi-core processors, virtual shared memory computer.

Data layout: A single global memory. Each thread reads global shared data and writes to a private fraction of global data.

Translation of the example parallel-for loop is given below.

Global:

#include "tbb/task_scheduler_init.h"
#include "tbb/blocked_range.h"
#include "tbb/parallel_reduce.h"
#include "tbb/cache_aligned_allocator.h"
using namespace tbb;

thread code:

struct sub1 {
   float ee;
   float *x, *y;
   sub1(float *xx, float *yy) : ee(0), x(xx), y(yy) {}
   sub1(sub1& s, split) { ee = 0; x = s.x; y = s.y; }
   void operator() (const blocked_range<int> & r){
     float e = ee;
     for (int i = r.begin(); i!= r.end(); ++i) {
       x[i] += ( y[i+1] + y[i-1] )*.5;
       e += y[i] * y[i];
     }
     ee = e;
   }
   void join(sub1& s) { ee += s.ee; }
};

main code:

task_scheduler_init init;
...
float e;
float *x = cache_aligned_allocator<float>().allocate(n+1);
float *y = cache_aligned_allocator<float>().allocate(n+1);
...
sub1 s(x, y);
parallel_reduce(blocked_range<int>(1, n, 1000), s);
e = s.ee;
...
cache_aligned_allocator<float>().deallocate(x, n+1);
cache_aligned_allocator<float>().deallocate(y, n+1);

In OpenMP shared memory parallel code annotations

OpenMP: Usually automatic paralleization with a run-time system based on a thread library.

A simplified translation of the example parallel-for loop is given below.

Global:

float e;

main code:

float *x = new float[n+1];
float *y = new float[n+1];
...
e = 0;
#pragma omp for reduction(+:e)
for (int i=1; i<n; ++i) {
   x[i] += ( y[i+1] + y[i-1] )*.5;
   e += y[i] * y[i];
}
...
delete[] x, y;

Other packages

We use On-Demand Virtual Single-Instruction-Multiple-Data (ODVSIMD) [1]to demonstrate how to implement DOACROSS parallelism. Based on the concept of DOACROSS parallelism, one thread (task) must have to wait until the others finish processing and continues itself.

Here is a program that has not been parallelized, C[i] has to get A[i-5] to process its statement. The dependence relationship is S1[i]-> T S2[i+5]

double A[N], B[M], C[N]
for ( i = 0; i < N; i ++) {/*loop to be parallelized */
  /* S1 statement */
  A[i] = B[i+2]/2;
  /* S2 statement */
  if ( i>4 ) C[i] = C[i] + A[i-5];
  }

Now, let's see the following program which has been parallelized in DOACROSS parallelism.

DOACROSS Parallelism Sample Code
double A[N], B[M], C[N]
VSIMD_enable(NO_THREADS); /* start of parallel execution */
Register base_A = &A[0], base_B = &B[0], base_C = &C[0];
/* tid=0.. NO_THREADS -1 */
Register tid = VSIMD_getVirtTid();
Register start = tid;
Register end = N;
Label1:
  Register double oper_A, oper_B, oper_C;
  Register offset_B = start << (3+LOG2_N);
  Register offset_A = start << (3+LOG2_N);
  offset_B += 16; /* i+2 */
  /* 8 byte load with latency */
  oper_B = load_1(base_B, offset_B);
  VSIMD_waitEvents(load_1);
  /* double divide with some latency */
  oper_A = oper_B / 2;
  write(base_A, offset_A, oper_A);
  /* signal all threads with sigID = start */
  VSIMD_signalAll(start);
  if (start > 4)
    /* wait for sig with sigID = start -5 */
    Register sigID = start – 5;
    VSIMD_waitSignal(sigID);
    Register offset_A5 = offset_A - 40;/*i-5*/
    oper_C= load_2(base_C, offset_A);
    oper_A= load_3(base_A, offset_A5);
    VSIMD_waitEvents(load_2, load_3)
    /* double add with some latency */
    oper_C= oper_C + oper_A;
    write(base_C, offset_A, oper_C);
  start+= NO_THREADS;
  if (start < end) goto Label1;
VSIMD_disable();/* end of parallel execution */

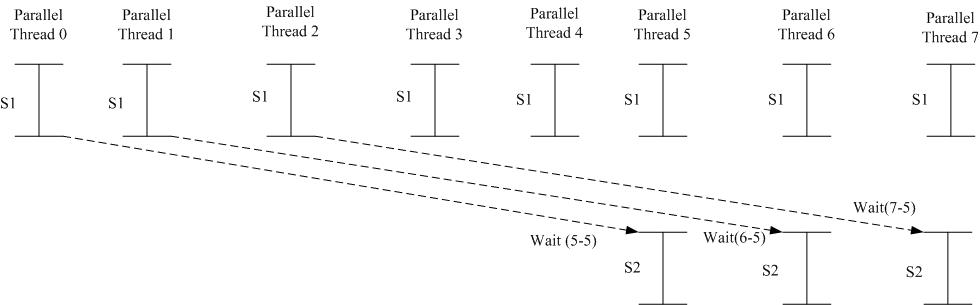
Obviously, if C[i] wants to process, C[i] has to wait until A[i-5]. In the previous sample code, VSIMD_signalAll(start); means all the threads have to wait and activate at the same time. So, all the threads will finish S1 and that means A[i] will be filled in value inside.

After all the threads finish S1, if (start > 4) means only if the number of threads bigger than 4 is allowed to process the following code. Register sigID = start – 5; and VSIMD_waitSignal(sigID); clearly points out to threads to go where to get the value of A[i-5].

From the previous sample code, only if (start > 4) fulfill the requirement that it will activate parallel process. This graph shows us that thread 5 has to wait thread 5-5, which means 0. The same to thread 6 that it has to wait 1 (6-5).

Finally, if (start < end) goto Label1; identifies if start has not attend end, then it will continue doing the following threads till all finish.

References

1. Wikipedia: Parallel Computing
2. FUNDAMENTALS OF PARALLEL COMPUTER ARCHITECTURE, Yan Solihin, Aug 2009
3. OpenMP.org
4. An Optimal Abtraction Model for Hardware Multithreading in Modern Processor Architectures
5. Intel Threading Building Blocks 2.2 for Open Source Reference Manual
6. NCSU CSC 506 Parallel Computing Systems
7. Sourceforge.net