CSC/ECE 506 Spring 2012/1b ps

Moore's Law

In 1965, Intel co-founder predicted that the number of transistors on a die would double every 24 months. This was a rough predictive statement that has brought Moore acclaim for its reputed accuracy and foresight. This article explores different interpretations of Moore's law, whether it has indeed held true across the years in all significant intervals of time, and whether it will hold true in the future.

The rate of growth Moore predicted is truly staggering. The equation form of the law is: T(t)=T0 * 2^(t/2) where T0 represents the initial transistor count in the start year and T(t) the transistor count in t years. Exponential growth is somewhat lost on transistors so we'll switch to counting something more tangible (and one most everyone understands): money. If one could double her wealth every 24 months and started with $1, she would have $5,931,641 in 45 years!

But this is exactly what Intel claims it has done with the transistor density of their processors (and certainly their bottom line). To a large extent, the company has symbiotically harnessed and fueled the public awareness of Moore's law to its advantage as a marketing device, but it is still valuable to study the context of the prediction (the 60s, the advent of semi-conductor technology and miniaturization) and the reasons Moore believed the prediction would hold and whether he was right.

Historic Context

According to David C. Brock in Understanding Moore's Law: four decades of innovation:

"By 1960 miniaturization was a fundamental issue for semiconductor technology and its industry. It had become, moreover, a central factor in the semiconductor community's discussions surrounding the new integrated circuits that had been touted in 1959 by Texas Instrucments as the first realization of the "monolothic" circuit ideal."

Two ideas are most striking about this statement: The focus on miniaturization and the concept of the "monolothic" circuit ideal.

In the early 1960s, the semi-conductor industry was gravitating towards building integrated circuits on wafers of silicon versus discrete transistors for use as components in electronic devices. The arguments presented were largely those based on cost reduction. Integrated or monolothic circuits were cheaper to produce than devices based on connected discrete transistors.

Among the seminal presentations of the time predating Moore's publication of Moore's Law is C. Harry Knowles (manager for Westinghouse's molecular electronics division). Knowles addressed two critical ideas that helps put Moore's Law into proper context: Knowles argued that with technological progress, devices could produce integrated circuits with greater functionality and complexity at higher yields (measure of output). (Brock). Secondly, Knowles brought attention to the issue of performance as a function of size.

Transistor Counts Over The Years

The stage was set: smaller was faster and miniaturized, integrated circuits were cheaper. Moore made several contributions to Knowles in his presentation of Moore's Law, including a significant simplification of ideas to transistor counts over time.

If Moore was right, he wasn't right on the first try. His initial prediction was that transistor counts would double every year. In 1975 he revised this prediction to every two years (credit: http://news.cnet.com/Myths-of-Moores-Law/2010-1071_3-1014887.html).

If we take 1971 and the Intel 4004 processor as our starting point, we see the following growth alongside the predicted growth and the variance and variance percentage next to each (credit for raw data: http://en.wikipedia.org/wiki/Transistor_count)

Processor	Transistor count	Year	Predicted Value	Variance	Percent Error (Variance/Predicted Transistor Count)
Intel 4004	2,300	1971	2,300	N/A
Intel 8008	3,500	1972	3,253	247	8%
Motorola 6800	4,100	1974	6,505	-2,405	-37%
Intel 8080	4,500	1974	6,505	-2,005	-31%
RCA 1802	5,000	1974	6,505	-1,505	-23%
MOS Technology 6502	3,510	1975	9,200	-5,690	-62%
Intel 8085	6,500	1976	13,011	-6,511	-50%
Zilog Z80	8,500	1976	13,011	-4,511	-35%
Motorola 6809	9,000	1978	26,022	-17,022	-65%
Intel 8086	29,000	1978	26,022	2,978	11%
Intel 8088	29,000	1979	36,800	-7,800	-21%
Motorola 68000	68,000	1979	36,800	31,200	85%
Intel 80186	55,000	1982	104,086	-49,086	-47%
Intel 80286	134,000	1982	104,086	29,914	29%
Intel 80386	275,000	1985	294,400	-19,400	-7%
Intel 80486	1,180,000	1989	1,177,600	2,400	0%
Pentium	3,100,000	1993	4,710,400	-1,610,400	-34%
AMD K5	4,300,000	1996	13,323,023	-9,023,023	-68%
Pentium II	7,500,000	1997	18,841,600	-11,341,600	-60%
AMD K6	8,800,000	1997	18,841,600	-10,041,600	-53%
Pentium III	9,500,000	1999	37,683,200	-28,183,200	-75%
AMD K6-III	21,300,000	1999	37,683,200	-16,383,200	-43%
AMD K7	22,000,000	1999	37,683,200	-15,683,200	-42%
Pentium 4	42,000,000	2000	53,292,093	-11,292,093	-21%
Barton	54,300,000	2003	150,732,800	-96,432,800	-64%
AMD K8	105,900,000	2003	150,732,800	-44,832,800	-30%
Itanium 2	220,000,000	2003	150,732,800	69,267,200	46%
Itanium 2 with 9MB cache	592,000,000	2004	213,168,370	378,831,630	178%
Cell	241,000,000	2006	426,336,740	-185,336,740	-43%
Core 2 Duo	291,000,000	2006	426,336,740	-135,336,740	-32%
Dual-Core Itanium 2	1,700,000,000	2006	426,336,740	1,273,663,260	299%
AMD K10	463,000,000	2007	602,931,200	-139,931,200	-23%
POWER6	789,000,000	2007	602,931,200	186,068,800	31%
Atom	47,000,000	2008	852,673,480	-805,673,480	-94%
AMD K10	758,000,000	2008	852,673,480	-94,673,480	-11%
Core i7 (Quad)	731,000,000	2008	852,673,480	-121,673,480	-14%
Six-Core Xeon 7400	1,900,000,000	2008	852,673,480	1,047,326,520	123%
Six-Core Opteron 2400	904,000,000	2009	1,205,862,400	-301,862,400	-25%
16-Core SPARC T3	1,000,000,000	2010	1,705,346,960	-705,346,960	-41%
Six-Core Core i7 (Gulftown)	1,170,000,000	2010	1,705,346,960	-535,346,960	-31%
8-core POWER7	1,200,000,000	2010	1,705,346,960	-505,346,960	-30%
Quad-core z196[3]	1,400,000,000	2010	1,705,346,960	-305,346,960	-18%
Quad-Core Itanium Tukwila	2,000,000,000	2010	1,705,346,960	294,653,040	17%
8-Core Xeon Nehalem-EX	2,300,000,000	2010	1,705,346,960	594,653,040	35%
Six-Core Core i7 (Sandy Bridge-E)	2,270,000,000	2011	2,411,724,800	-141,724,800	-6%
10-Core Xeon Westmere-EX	2,600,000,000	2011	2,411,724,800	188,275,200	8%

Data Review

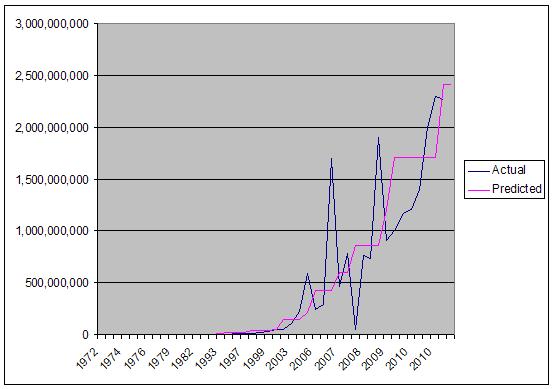
So it's quite clear that the "law" is not to be taken too literally. It's a general marker for what to expect in upcoming years. One sees actually that the number jumps in several years to catch up (by 2011, the variance is only %8 with the 10-Core Xeon chip). The Dual Core Itanium also lurches forward nearly %300.

The following chart shows the actual and predicted transistor counts:

Variance Years

We see that there are probably exceptions which should be taken out of the data; for example, the Atom processor, which is an ultra-low voltage processor embedded in netbooks. These are special purpose processors that do not reflect the state of the technology at the time (for example, the Intel Core i7 chip in 2008, the same year as the Atom chip, is closer to the mark at a variance of only -14%, versus the Atom's -94%.

So it is important when evaluating whether Moore's law has failed to hold to compare chips of the same family, or perhaps take the best technology for a given year. For example, in years 1979, 1982, 1985, 1989 with the Motorola 68000, Intel 80286, Intel 80386 and Intel 80486, the best chips available in the data above, either exceed Moore's predictions or come very close.

But there are many intervals where this is not true, including 1971-1978, 1993-2000, which show poor performance. One explanation is that other chip factors started to become more important during this time (power consumption, for example). One also sees certain chips and chip families which cause transistor counts to lurch forward (for example, the first Itanium 2 which included 221 million transistors, 4 times Moore's prediction for 2006). This lurching forward may have an effect that for subsequent years, the hardware outstrips market needs and it takes some time for operating systems and software to catch up. During this period, there is less demand for more powerful chips so market forces require the production of less expensive chips with lower transistor counts.

Moore's Law - The Future

With a good survey of data and historic context firmly in view, we can now consider whether Moore's Law will hold in future years. Clearly, Moore's predictions concerned transistor counts, not processor speed. But like Knowles, Moore was searching for a simple metric of complexity and performance with respect to cost. His ultimate aim was to predict future performance at costs that were feasible in the marketplace. Hence, on the one hand, one can take Moore's Law to apply to performance versus the specific metric of transistor counts.

Performance is a function of many factor besides transistor counts, including memory management and overall processor architecture (pipelining, cache levels, etc.). Still, in the context of miniaturization and monlithic architectures, it is possible that Moore underestimated the importance of these factors despite his ultimate interest in the sustained future improvement in performance with respect to cost. We must also consider that, as with any new technology, the semi-conductor industry was struggling to convince the engineering community and public of the importance of integrated circuits. The focus was deliberate and simple: adopt integrated circuits as the future.

Those who argue that transistor counts will eventually hit a wall typically do so on the basis of physical limitations. The arguments seem reasonable given that Moore's prediction concerned the number of transistors on a single die and the general unsustainability of exponential growth. Even if the physical limitations were surmounted by better materials and semi-conductor manufacturing processes, it is likely their benefits will be outweighed by alternative innovations at other levels.

The exponential growth predicted by Moore's law is ultimately not sustainable, even as a rough guideline. Even if it were and the above physical limitations are overcome, the resulting transistor count or performance improvement will likely also significantly outrun Moore's predictions since the technology to work with materials at an atomic level will likely lead to completely different architectures Moore could never have predicted.

References

<references> Understanding Moore's law: four decades of innovation By David C. Brock </references>