CSC/ECE 506 Spring 2012/ch2b cm

Take a modern GPU architecture, and use it as an example in explaining how data-parallel programming is done. Do this in a discussion similar to the discussion of the hypothetical array processor in Lecture 3. That is, describe the problem, then describe the instructions of the GPU, and show code for how the problem can be solved efficiently using GPU instructions. You might want to use multiple examples to illustrate different facilities of a GPU instruction set.

Introduction

This article provides an overview of data parallelism and how modern GPUs (specifically NVidia GeForce/CUDA architecture) exploit it to achieve super computing capabilities. It provides a brief discussion of the commonly encountered problems that necessitate the application of parallel computing techniques. It illustrates some of the facilities made available by these architectures which should be enough to get you started with basic GPU programming.

Why GPUs

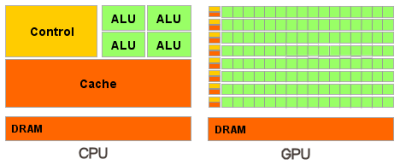
If we look at the modern CPUs and GPUs, and compare their performance (in terms of floating point capability) (-link-), we notice that GPUs clearly outclass their competitors by a huge margin. This is because GPU is specialized for compute-intensive, highly parallel computation – which is what graphics rendering is all about – and therefore designed such that more transistors are devoted to data processing rather than data caching and flow control (as the following diagram illustrates). Specifically, GPU is best suited for data parallel (-link-) applications, with high arithmetic intensity – the ratio of arithmetic operations to memory operations. Since a same set of instructions are executed for each data element, there's a minimal need of flow control and the high arithmetic intensity can overshadow the latency incurred in memory accesses.

Some Basics

C Runtime overview

This section aims to describe basic C programming model provided by NVidia CUDA architecture and to some extent the APIs provided for parallel programming.

Kernels

Kernels are similar to C functions, except that they are executed N times parallely on N CUDA threads instead of only once like regular C functions. Kernels are declared using __global__ specifier and the number of threads to execute is specified using the "execution configuration" <<<...>>> syntax. Each thread that executes within a kernel is given a unique identifier (obtained using threadIdx variable). Specific examples of using these abstractions follow in the next section.

Thread Hierarchy

Unlike threads in regular Operating systems, CUDA provides programmers to arrange the threads in 1 dimension, 2 dimension and 3 dimension structures called Blocks. Hence the threadIdx variable is actually a 3 component vector, i.e threadIdx.x, threadIdx.y, threadIdx.z may be used to access a particular thread (x,y,z) in the 3D block. This provides programmers a natural way to perform parallel computations in domains such as Arrays,Matrices and Volumes.

Blocks in turn can co exist with other blocks of threads, where a group of blocks is termed as Grid. Again blocks can be arranged in 1 dimension, 2 dimension and 3 dimension structures within a Grid and hence enable creation of large number of parallel threads that work in multiple dimensions of data. A thread may access the unique block Id in which it is running by using the variable blockIdx. Thread blocks are required to execute independently: It must be possible to execute them in any order, in parallel or in series. This independence requirement allows thread blocks to be scheduled in any order across any number of cores.

An important requirement of a parallel programming model is providing a way to synchronize between the threads. This is typically done by inserting synchronization barriers in the program. CUDA allows programmers to specify synchronization points in the Kernel using the light weight __synthreads() function.

Memory Hierarchy

As mentioned above, memory access latency is not a major concern for data parallel applications. But still a good architecture strives to provide fast, efficient memory access to thousands of threads that run in parallel. In CUDA, each thread has access to local memory and fast shared memory, visible to all threads within a block and with same lifetime as the block. All threads also have access to a global device memory which is somewhat slower. There are also two additional read-only memory spaces accessible by all threads: the constant and texture memory spaces, which are optimized for different memory usage patterns. The global, constant, and texture memory spaces are persistent across kernel launches by the same application.

Traditional Problem

Following is a most elementary problem that illustrates the essence of data parallelism. It involves computing the addition of two vectors and storing the result into a third vector. A standard C program to achieve this would look like this:

int main()
{
	float A[1000],B[1000],C[1000];
	.....	
	//Some initializations
	.....

	for(int i = 0; i < 1000; i++)
		C[i] = A[i] + B[i];

	......
}

Here we are executing the for loop, once for each array index. On a sequential processor (Single core processor),the instructions similar to the following are executed for each run of the for loop.

Fetch i
Fetch A[i] into Register EAX
Fetch B[i] into Register EBX
Add EBX to EAX
Store EAX into Adress of C[i]

Hence the time taken to perform this simple computation is linear in the size of the input. This could manifest as a major bottleneck in real time applications such as 3D renderings, Face recognition, Monte Carlo simulation,etc where the input to be processed is embarrassingly large.

Solution

The pattern that exists in all of these problems is that, there's one instruction or a single set of instructions that act on a large amount of distinct data elements (SIMD - link). This is a typical pattern where data parallelism can be applied.

In a two processor (or two core) system, we could have both the processing units (cores) work on a part of the array simultaneously. Following snippet is a rough outline of how this could be achieved:

.....
    if CPU = "a"
       lower_limit := 0
       upper_limit := round(A.length/2)
    else if CPU = "b"
       lower_limit := round(A.length/2) + 1
       upper_limit := A.length

for i from lower_limit to upper_limit by 1
   C[i] = A[i] + B[i];
.....

This is typically done in high level programming languages such as C using the Thread(-link-) abstraction, where each thread runs simultaneously on a different processing unit. Even though this solution is much faster, it is still limited to just two parallel executions.

GPU solution

Because the same program (set of instructions) is executed for each data element, there is a lower requirement for sophisticated flow control, and because it is executed on many data elements, it exhibits high arithmetic intensity. GPU is specialized for compute-intensive, highly parallel computation – exactly what graphics rendering is about – and therefore designed such that more transistors are devoted to data processing rather than data caching and flow control. Hence GPU (more specifically CUDA) would be the best answer to such a problem.

Similar to what we did with the two processor, multi-threaded solution, CUDA enables us to create thousands of threads and run them parallely on thousands of Processing units that GPU provides. Following C program illustrates how this can be achieved:

__global__ void VecAdd(float* A, float* B, float* C)
{
	int i = threadIdx.x;
	C[i] = A[i] + B[i];
}

int main()
{
	...
	// Invocation with N threads
	VecAdd<<<1, 1000>>>(A, B, C);
	...
}

In this code, the main function simply calls a specialized routine (called Kernel (-link-)), and passes in the 3 arrays that need to be processed parallely. It also informs the CUDA runtime (-link-) to create 1000 threads, where each thread runs the same VecAdd routine, but on different data. As can be seen from the code, in the VecAdd routine, we are finding the thread index and acting only on that index of the input arrays. Hence each of the 1000 threads acts on a different location and performs the computation. This helps us achieve exponential performance improvements, which becomes evident when dealing with super-parallel applications such as those mentioned above.

Slightly Evolved Problem

Let us increase slightly the complexity of the above problem. Consider the program that adds two NxN matrices. A simple CPU program to achieve this may look like this:

void add_matrix( float* a, float* b, float* c, int N ) 
{ 
	int index; 
	for ( int i = 0; i < N; ++i ) 
	for ( int j = 0; j < N; ++j ) 
	{ 
		index = i + j*N; 
		c[index] = a[index] + b[index]; 
	} 
} 
 
int main() 
{
    add_matrix( a, b, c, N );
}

As discused before, CUDA provides a hierarchy of threads, which can be exploted to achieve fast parallel computation in 2D and 3D as well. In order to achieve data parallelism in 2D or 3D, we can use the 3 components (x,y,z) of threadIdx variable.For a two-dimensional block of size (Dx, Dy), the thread ID of a thread of index (x, y) is (x + y Dx); for a three-dimensional block of size (Dx, Dy, Dz), the thread ID of a thread of index (x, y, z) is (x + y Dx + z Dx Dy). Based on this idea, the following code adds two NxN matrices in parallel:

__global__ void MatAdd(float A[N][N], float B[N][N],float C[N][N])
{
	int i = threadIdx.x;
	int j = threadIdx.y;
	C[i][j] = A[i][j] + B[i][j];
}
int main()
{
	...
	// Invocation with one block of N * N * 1 threads
	int numBlocks = 1;
	dim3 threadsPerBlock(N, N);
	MatAdd<<<numBlocks, threadsPerBlock>>>(A, B, C);
	...
}

MatAdd kernel here performs the N*N additions almost at the same time, assuming the GPU has so many processing entities. Hence the performance boost obtained is easily exponential as compared to regular CPU computation.

Some interesting Applications

Password guessing 3D rendering,etc http://www.infoworld.com/d/developer-world/gpu-computing-about-massive-data-parallelism-263