CSC/ECE 506 Spring 2012/1c 12

MISD

Micheal J. Flynn introduced the idea of an MISD (Multiple Instruction, Single Data) computer architectures in his original taxonomy in 1966.^[1]

The MISD Architecture

Dr. Yan Solihin defines MISD as "..an architecture in which multiple processing elements execute from different instruction streams, and data is passed from one processing element to the next."^[2] He also notes that MISD architectures are restricted to certain types of computations due to the requirement of data-passing between processing elements.^[2] Each processing element executes different instructions on the data stream.^[3] Every time the data is processed by a processing element, we can always argu that the data is no longer the original data introduced at the start of the stream.^[4]

From NCSU CSC/ECE 506 Spring 2012 Lecture 1 notes^[5].

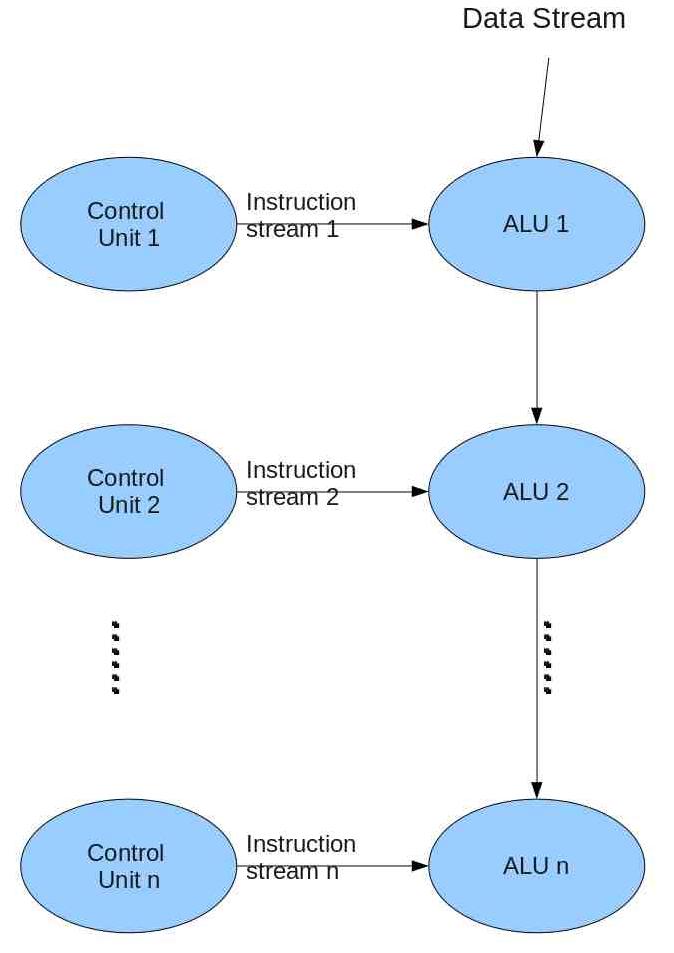
From this image, we see that the data stream has one clear entrance and exit into the system. What we are unsure of is if each processing element has access to a collective instruction storage or if all processing elements are embedded with an individual instruction storage. Depending on the specific system described, each processing element is generally function specific or predestined; but in some systems (similar to iWarp), each processing element may be quite advanced.

From Flynn's paper "Very High-Speed Computing Systems," 1966^[14].

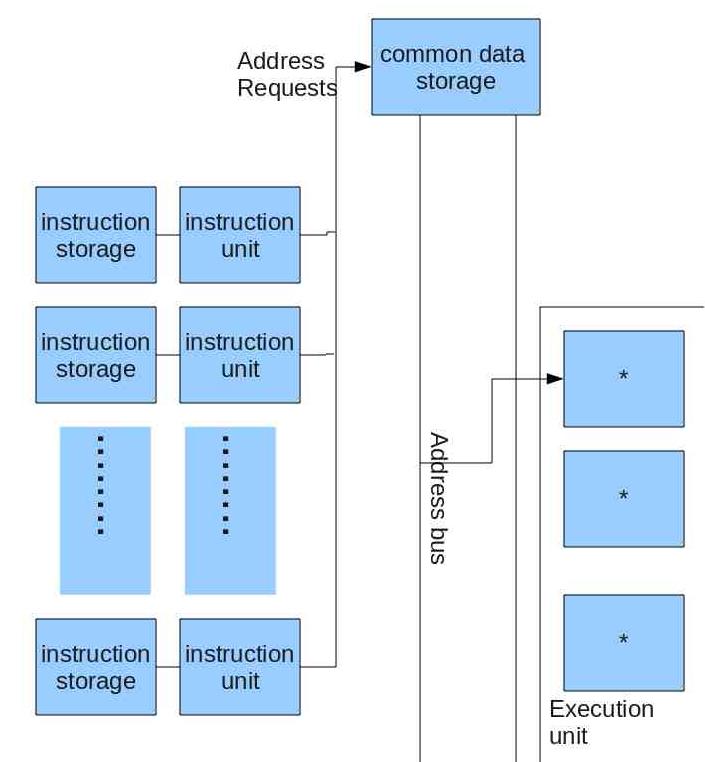
For this image, Flynn describes each processing element as an independent virtual machine that operates on independent program sequences. He explicitly states that each processing element has it's own private instruction memory, which limits the data stream as being the only interaction between instruction streams.^[14]

From Flynn's paper "Very High-Speed Computing Systems," 1966. "Under such an arrangement, only the first execution unit sees the source data stream and while it is processing the ith operand, the ith execution unit is processing the ith derivation of the first operand of the source stream."^[14]

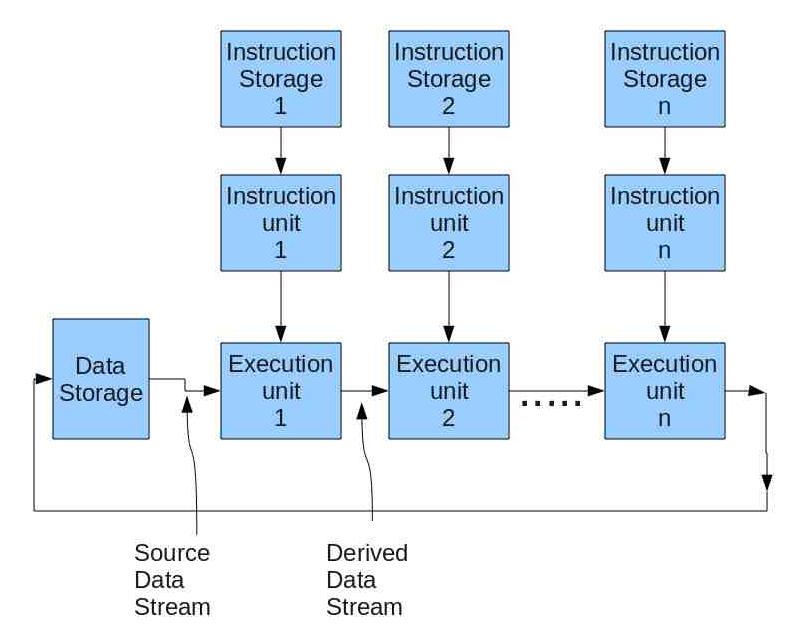
In this image, Flynn demonstrates a version of MISD in which the data stream is a force forwarding of operands between the execution units. An instruction that any individual execution unit sees can be fixed (flexible setup of units), semi-fixed (one pass of a data file), or variable (stream of instructions could operate on any point of the data stream)^[14].

MISD Computers

While it is widely believed that no actual MISD computer exists in practice, it is controversially argued that a systolic array is the most common example of MISD^[6].

Some arguments exist that pipelined vector processors could be considered an example of MISD architecture due to the fact that a different operation is performed on the data stream as it flows from stage to stage^[6]. The argument against this idea is that individual processing elements in each stage do not technically fetch their operations from an instruction cache^[6], but are more similar to a function specific, or ASIC, chip.

One application that exists for MISD VLSI architectures are applications which require multiple pattern matching in large data streams that lack any preprocessed indexes for lookups^[8]. This research presents a set of recursive query semantics: "concatenation of basic strings and patterns, alphanumerical comparisons of simple strings, boolean operations on subexpressions, and hamming distance filtering"^[12], and then explains that the recursion process of the semantics is best understood as a "..recursion tree where the result is found by propagating the results from the leaf nodes...to the root of the tree"^[12].

Recently, Stanford University and Maxeler Technologies have been working on acceleration methodologies that benefit from combining different computer architectures. One of the proposed methodologies based on FPGA arrays uses SIMD for multiple data strips until the pin bandwidth limits the acceleration, then switches to an MISD-style pipeline of the FPGA arrays until acceleration is limited by circuit limitations^[13].

Systolic Array

"A systolic array is an arrangement of processors in an array (often rectangular) where data flows synchronously across the array between neighbors"^[7] Systolic arrays have data processing units (DPU) arranged in the form an matrix such that they are connected to their neighbors in the form of a mesh^[9]

The two models of systolic arrays are shown below:

From Wikipedia article about systolic array^[10].

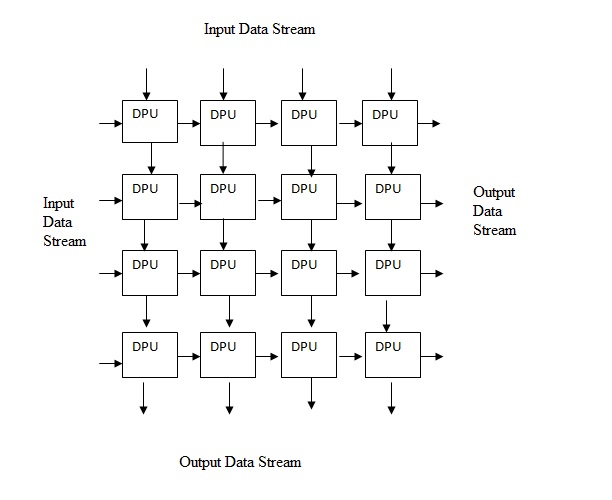
The above diagram represents a systolic array where each DPU performs a specific operation on the data which can be input/output from an external source in the case of embedded systems or could be system generated by a auto sequencing memory unit. Each DPU performs a different computation based on the instruction set given to it and takes in data from the top or the left and then outputs it to it's right or below. A systolic array may or may not have local memory based on the application it is being used for.

An example of an application of systolic array is a matrix multiplication. The systolic array can have a 4X4 mesh to multiply two 4X4 matrices where the data of all the rows and columns to be multiplied can be entered as the input into each DPU and the instruction executed by each DPU would be to multiply the incoming stream of numbers and add them to a previous value stored in it if there is any. The final output that is the resultant matrix would be the values stored in each DPU.

Systolic arrays can be used to make algorithms involving a lot of parallel computation much easier. "Systolic array processors have been known to be extremely efficient at executing the class of algorithms that exhibit tight coupling between neighboring cells via data transfers in an N-dimensional model space" ^[11]

Applications of Systolic Arrays

The various complex problems that can be solved efficiently using systolic arrays are

• Fast Fourier Transforms
• Convolutions
• Dynamic time wraping
• Video Filtering
• Data compression
• Image processing
• Signal processing
• Differential equations

11.Robert E. Morley, Jr.Thomas J. Sullivan ,"A Massively Parallel Systolic Array Processor System",in Electronic Systems and Signals Research Laboratory,Department of Electrical Engineering,Washington University, pp:217.

References

1. Flynn, M. (1972). "Some Computer Organizations and Their Effectiveness". IEEE Trans. Comput. C-21: 948.
2. Solihin, Y. (2008). "Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems". Solihin Publishing & Consulting LLC. C-1: 12.
3. CSC 8383 Lecuture 5
4. MISD wiki
5. ECE506 Spring 2012 Lecture 1
6. 3.1.3 MISD Computers
7. Laiq hasan,Yahya M.Khawaja,Abdul Bais,"A Systolic Array Architecture for the Smith-Waterman Algorithm with High Performance Cell Design" in IADIS European Conference Data Mining, 2008, pp. 37
8. Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 12, no. 7, July 2004, pp. 727
9. Systolic array
10. Systolic array architecture
11. Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 12, no. 7, July 2004, pp. 728
12. Michael Flynn, R. Dimond, O. Mencer, O. Pell, "Finding Speedup in Parallel Processors," in International Symposium on Parallel and Distributed Computing, 2008, pp. 3
13. Michael J. Flnn, "Very High-Speed Computing Systems," Proceedings of the IEEE, vol. 54, no. 12, December 1966, pp.1908