CSC/ECE 506 Spring 2011/ch4a ob: Difference between revisions
| Line 23: | Line 23: | ||
*Reflection | *Reflection | ||
Xr = (1+ α)Xcen- | Xr = (1+ α)Xcen- αXn | ||
After calculating the reflection point(Xr), we evaluate the function (Yr) value at this point. If it is an improvement over the minimum function value, we continue in the same direction and calculate the expansion point. | After calculating the reflection point(Xr), we evaluate the function (Yr) value at this point. If it is an improvement over the minimum function value, we continue in the same direction and calculate the expansion point. | ||
| Line 35: | Line 35: | ||
If Yr is not an improvement over the minimum function value, then we go in the other direction and calculate the contraction point(Xc). | If Yr is not an improvement over the minimum function value, then we go in the other direction and calculate the contraction point(Xc). | ||
Xc = | Xc = βXn+(1-β)Xcen | ||
If Yc is an improvement over the minimum function value, then Xc replaces Xn to form the new simplex. | If Yc is an improvement over the minimum function value, then Xc replaces Xn to form the new simplex. | ||
| Line 41: | Line 41: | ||
*Reduction | *Reduction | ||
If the contraction point is not an improvement either, then we shrink / reduce the entire simplex towards the best point Xo. | If the contraction point is not an improvement either, then we shrink / reduce the entire simplex towards the best point Xo. | ||
Xi = | Xi = X0+ σ (Xi-Xl) ∀ i=1….N | ||
*Widely used Coefficient Values: | *Widely used Coefficient Values: | ||
Revision as of 03:39, 28 February 2011
Introduction
The Nelder Mead Algorithm is a simplex method for function minimization developed by J. A. Nelder and R. Mead in 1965[2]. The method is used for minimizing an 'N' dimensional function, by comparing the function values at n+1 vertices of a simplex, followed by the replacement of the vertex with highest function value by another vertex having a lower function value. The algorithm, by itself is highly serial in nature.
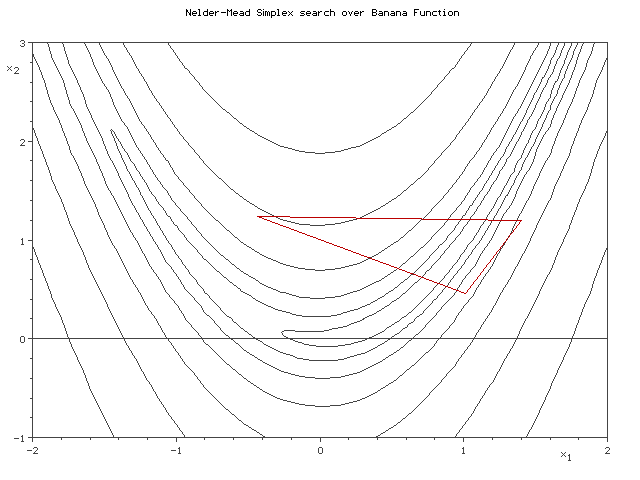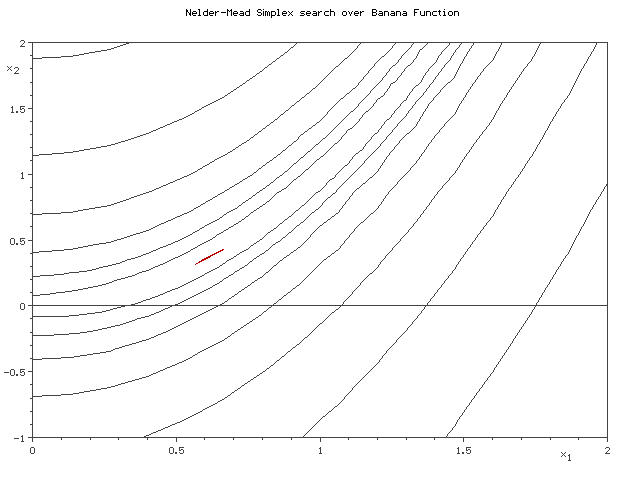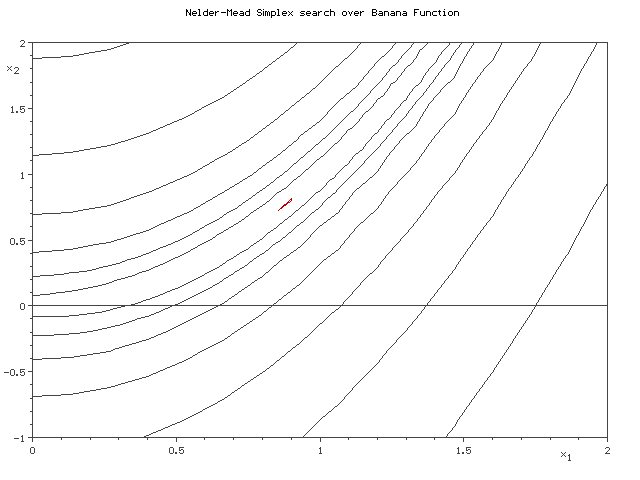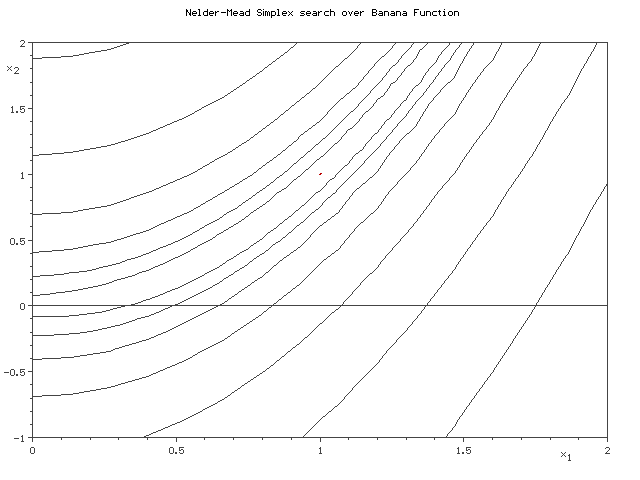
In this article, we will discuss the Serial Nelder Mead Algorithm and its parallelization at Algorithmic level and Task Level. The figure below demonstrates how Nelder Mead minimizes a two dimensional banana function using a 3 point simplex.
Serial Nelder Mead Function Minimization Algorithm (Serial Simplex Method)
For an ‘n' dimensional function, we start with a simplex of ‘n+1’ arbitrary points in an ‘n’ dimensional space. Let these points be X0 … Xn and the corresponding function values be Y0 to Yn. Thus, to store the entire simplex we will need an n+1 x n array for the points and an array of size n for the Function values. Let us briefly discuss what is done in a single step of the algorithm.
Single Step of the Nelder Mead Algorithm:
At each step of the algorithm we perform six operations – Ordering, Centroid, Reflection, Expansion, Contraction and Reduction.
- Ordering of Simplex
We sort the simplex in ascending order by function values. i.e. X0 would be the point with lowest function value and Xn would be the point with highest function value.
- Centroid Calculation
After ordering, we calculate the centroid of all but the worst point (Xn) in the current simplex.
Xcen = 1/N ∑ Xi for i = 0,1 .... N-1
- Reflection
Xr = (1+ α)Xcen- αXn
After calculating the reflection point(Xr), we evaluate the function (Yr) value at this point. If it is an improvement over the minimum function value, we continue in the same direction and calculate the expansion point.
- Expansion
Xe = γXr+(1-γ)Xcen
If the expansion point(Xe) is an improvement, then Xe replaces the worst Point Xn and a new simplex is formed. If the expansion point is not an improvement, then Xr replaces Xn and the new simplex is calculated.
- Contraction
If Yr is not an improvement over the minimum function value, then we go in the other direction and calculate the contraction point(Xc).
Xc = βXn+(1-β)Xcen
If Yc is an improvement over the minimum function value, then Xc replaces Xn to form the new simplex.
- Reduction
If the contraction point is not an improvement either, then we shrink / reduce the entire simplex towards the best point Xo. Xi = X0+ σ (Xi-Xl) ∀ i=1….N
- Widely used Coefficient Values:
α=1 ,γ=2 ,β=0.5 ,σ= -0.5
This process is repeated till we reach a predetermined acceptable value for the function minima.
Shown below is an example pseudo code for the Serial Nelder Mead Algorithm.
Serial Code
int N;
float X[N+1][N+1]; // N+1 Points, each with N+1 coordinates.
float Y[N+1]; // Function values for N+1 points. (this is a function of X)
float Y_max_allowed; // termination condition
float Ycen, Xcen[N+1]; // centroid
float Yr, Xr[N+1]; // reflection point
float Yc, Xc[N+1]; // contration point
float Ye, Xe[N+1]; // expansion point
Nelder_Mead()
{
done = 0;
Sort_Simplex();
while(!done)
{
Calculate_Centroid();
Calculate_new_point();
Sort_Simplex();
Check_done();
}
}
Sort_Simplex()
{
Comparison sort of N+1 numbers,
Ascending order by function value
}
Calculate_Centroid()
{
for i = 0 thru N do // For all Dimensions
for j = 0 thru N-1 do // Centroid of all but worst point
Xcen[i] += X[i][j];
end for
Xcen[i] /= N;
end for
}
Calculate_new_point()
{
// reflection
for i = 0 thru N do
Xr[i] = (1+alpha)Xcen[i] – alpha*X[N][i];
// expansion
for i = 0 thru N do
Xe[i] = gamma*Xr[i] + (1- gamma)Xcen[i];
//contraction
for i = 0 thru N do
Xe[i] = beta*X[N][i] + (1- beta)Xcen[i];
// accept one of the points based on their function values
// as described in the section above
// If none of the values is better, shrink the simplex based on X0
for i = 0 thru N-1 do
for j = 0 thru N do
X[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]);
end_for
end_for
}
Check_done()
{
// stop if the lowest function value is small enough
if(Y[0] <= Y_max_allowed)
done = 1;
}
Parallel Nelder Mead Function Minimization Algorithm
Parallelization at Algorithm Level (Parallel Simplex Method)
Each Processor is assigned parameters corresponding to one point in the simplex. The processors then conduct simplex search steps (as in the serial version) to find a better point. On completion, the processors communicate the new points to form a new simplex. Let us assume that the degree of parallelization is P. Bear in mind that P is may or may not be equal to the number of available processors. For simplicity, let us assume that there are P processors. For 1 processor, this algorithm will be equivalent to the serial algorithm. We first create a simplex of N+1 points and assign each processor, one of the P worst points and distribute rest of the (N+1 –P) points across all the processors. Then each processor goes through an entire step of the Nelder Mead algorithm. P processors return P improved points, which replace the P worst points in the original simplex. The new simplex is again sorted and divided in the same way. Lee & Wiswall [3] provides adequate proof that the parallel algorithm converges as well as the serial algorithm does and that the performance gain reaches saturation after P = N/2. Note that this does not take into account parallelism at task level.
Parallelization at Task Level
The Nelder Mead algorithm can be parallelized for each individual task, e.g. ordering, centroid calculation, etc. This parallelism is independent of the parallelism at algorithmic level.
Data Parallel Implementation
It can clearly be seen from the serial code that some of the statements like function calculation for every point, calculation of coordinate values for each dimension of the centroid and other points, exhibit DOALL data parallelism, i.e. they are independent of each other and can be performed all at once. The code for that can be given as follows, by replacing the for loops by for_all loops:
int Nprocs;
Nelder_Mead()
{
done = 0;
Sort_Simplex();
while(!done)
{
Calculate_Centroid();
Calculate_new_point();
Sort_Simplex();
Check_done();
}
}
Sort_Simplex()
{
Comparison sort of N+1 numbers,
Ascending order by function value
}
Calculate_Centroid()
{
DECOMP X[i][j](CYCLIC,*,Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do // For all Dimensions
DECOMP X[i][j](*,CYCLIC, Nprocs) // decompose into tasks for each processor
for_all j = 0 thru N-1 do // Centroid of all but worst point
myXcen[i] += X[i][j]; // private variable for each accumulate
end for_all
REDUCE(myXcen[i],Xcen[i],ADD) ; // reduction operator for Centroid
Xcen[i] /= N;
end for
}
Calculate_new_point()
{
// reflection
DECOMP Xr[i] (CYCLIC, Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do
Xr[i] = (1+alpha)Xcen[i] – alpha*X[N][i];
// expansion
DECOMP Xe[i] (CYCLIC, Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do
Xe[i] = gamma*Xr[i] + (1- gamma)Xcen[i];
//contraction
DECOMP Xc[i] (CYCLIC, Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do
Xc[i] = beta*X[N][i] + (1- beta)Xcen[i];
// accept one of the points based on their function values
// as described in the serial section above
// If none of the values is better, shrink or reduce the simplex based on X0
DECOMP X[i][j](CYCLIC,*,Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N-1 do
DECOMP X[i][j](*,CYCLIC, Nprocs) // decompose into tasks for each processor
for_all j = 0 thru N do
X[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]);
end_for_all
end_for_all
}
Check_done()
{
// stop if the lowest function value is small enough
if(Y[0] <= Y_max_allowed)
done = 1;
}
In the shared memory implementation of the algorithm, we use lock () and unlock () commands to make sure that multiple threads do not write to the same memory location at a given time. Only one thread can be in the critical section of the program at a given time. Let us take an example of the function to calculate the centroid and parallelize it. As shown in the code below, The centroid array needs to be a shared variable since multiple threads will be updating it. We use a lock and unlock around it so that no more than one thread tries to modify it at the same time. After waiting for all the updates from different threads to be done, we proceed ahead.
shared float Xcen[N];
Calculate_Centroid()
{
for_all i = 0 thru N do // For all Dimensions
//The J LOOP and centroid update be broken down into P threads
// with each thread workingon N+1/P points
for_all j = 0 thru N-1 do // Centroid of all but worst point
myXcen[i] += X[i][j]; // private variable for each accumulate
end for_all
LOCK(Xcen[i]) // update centroid using the value from each thread
Xcen[i] += myXcen[i];
UNLOCK(Xcen[i]);
WAIT_FOR_END(nprocs-1); // we wait for all threads to update the centroid
Xcen[i] /= N;
end for
}
Similar method can be used to parallelize all the other functions like sorting and new point calculation.
Message Passing Implementation
In Message passing , thread division would be similar to that of the shared memory model, except that each thread has its own private memory and data updates are made by messaging, Lets consider the centroid function once again. Here, myXcen variable for each thread will be updated by values received from other threads and each thread will send its own updated value to the others.
Calculate_Centroid()
{
for_all i = 0 thru N do // For all Dimensions
//The J LOOP and centroid update be broken down into P threads
// with each thread workingon N+1/P points
for_all j = 0 thru N-1 do // Centroid of all but worst point
myXcen[i] += X[i][j]; // private variable for each accumulate
end for_all
SEND(Xcen[i], to all other procs) // send updated values to other processors
Xcen[i] += myXcen[i];
RECEIVE(Xcen[i], from all other procs); // get updated values from other processors
Xcen[i] /= N;
end for
}
Similar method can be used to parallelize all the other functions like sorting and new point calculation.
References
1. Nelder Mead Method
2. Nelder, J. A., and R. Mead (1965): “A Simplex Method for Function Minimization,” Computer Journal, 7, 308–313
3. Donghoon Lee, Matthew Wiswall (2007):"A Parallel Implementation of the Simplex Function Minimization Routine," Journal, Computational Economics, Volume 30 Issue 2
4. CSC/ECE 506 Spring 2011 Lecture 7 Notes, by Dr. Edward Gehringer