CSC/ECE 506 Spring 2011/ch4a zz

Introduction

N-body Problem. Picture source: NASA

The N-body problem stated as follows: Select the position and velocity of n celestial bodies as states. Given the initial condition of of N bodies, compute their states at arbitrary time T. Normally a three-dimensional space is considered for N-body problem. There is a simplified N-body problem called restricted N-body problem where the mass of some of the bodies is negligible. Several remarkable three-body simulation can be found in [1].

The trajectory of restricted three-body system from[1].

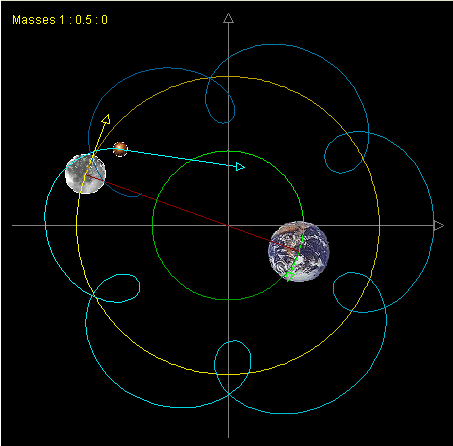
Many mathematicians have proofed that it is impossible to find a general solution for n-body problem analytically[2][3]. The system could become unstable very easily. However, the problem can be solved numerically. The most common approach is to iterate over a sequence of small time steps. Within each time step, the acceleration on a body is approximated by the transient acceleration in the pervious time step. The transient acceleration on a single body can be directly computed by summing the gravity from each of the other N-1 bodies. While this method is conceptually simple and is the algorithm of choice for many applications, its O(N²)

The simulation of N-body system can be used from simulation of celestial bodies (gravitational interaction)to interactions of a set of particles (electromagnetic interaction).

Parallel N-body problem

Since each particle will interact with others by the force of gravity, the simulation of N-body system is computationally expensive for large numbers of N. There a O(N²) interactions to compute for every iteration. Furthermore, in order to have a accurate result, the discrete time step must relatively small. Thus, there has been a huge interest in faster parallel algorithm for N-body problem.

data-parallel

In 1985, Appel took the first step of decomposes the problem by introducing a tree structure[4]. His data-parallel algorithm reduced the order time of the algorithm from O(N²) to O(N logN). In the next year, Barnes and Hut extend the tree-based force calculation with logarithmic growth of force terms per particle[5].

For each time step:
1. Build the BH tree.
2. Compute centers-of-mass bottom-up
3. For each body
   Star a depth-first traversal of the tree; 
   Truncating the search at internal nodes where the approximation is applicable;
   Update the contribution of the node to the acceleration of the body.
4. Update the velocity and position of each body.

References

[1] [1] Collection of remarkable three-body motions

[2][[2]] something about Poincaré

[3] Diacu, F (01/01/1996). "The solution of the n-body problem". The Mathematical intelligencer (0343-6993), 18 (3), p. 66.

[4] A. Appel, "An Efficient Program for Many-Body Simulation", SIAM J. Scientific and Statistical Computing, vol. 6, 1985

[5] Barnes. Josh, Hut. Piet, (12/04/1986). "A hierarchical O(N log N) force-calculation algorithm". Nature (London) (0028-0836), 324 (6096), p. 446.