CSC/ECE 506 Spring 2010/ch 3 yl

Supplement to Chapter 3: Support for parallel-programming models. Discuss how DOACROSS, DOPIPE, DOALL, etc. are implemented in packages such as Posix threads, Intel Thread Building Blocks, OpenMP 2.0 and 3.0.

Parallel-programming models

Loop-independent vs. loop-carried dependences

Before performing the three kinds of parallelism analysis, we need to discuss about loop-dependence analysis first.

Statement dependences

To discuss code analysis, let's define the framework as follows. Let S denote a statement in the source code. Let [] denote loop iteration space. Let S1 -> S2 denote statement S1 executes before S2. Then, we further define three statement dependences:

• S1 ->T S2 denotes true dependence: S1 -> S2, and S1 writes to a location that is read by S2.
• S1 ->A S2 denotes anti dependence: S1 -> S2, and S1 reads a location written by S2.
• S1 ->O S2 denotes output dependence: S1 -> S2, and S1 writes to the same location written by S2.

To give a better understanding, we illustrate the dependences using the code section below:

for (i=1; i<N; i++)
    S1: a[i] = i;
    S2: b[i] = a[i-1];
    S3: b[i] = a[i]+c[i+1];
    S4: c[i] = 2*i;

The dependences corresponding to the code are:

• S1[i-1] ->T S2[i]: a[i-1] is written in statement S1 in the (i-1)th iteration, and read in S2 in the ith iteration.
• S1[i] ->T S3[i]: a[i] is written in statement S1 in the ith iteration, and read in S3 in the ith iteration.
• S3[i] ->A S4[i+1]: c[i] is read in statement S3 in the ith iteration, and written in S4 in the (i+1)th iteration.
• S2[i] ->O S3[i]: b[i] is written in statement S2 in the ithe iteration, and also written in S3 in the ith iteration.

Loop-independent dependences

Loop-independent dependence is defined as a dependence that exists between statements within a loop iteration. Use the example code section above again to illustrate this definition.

• S1[i] ->T S3[i]: loop-independent dependence. Because a[i] is written in S1 in the ith iteration, and read in S3 in the same iteration.
• S2[i] ->O S3[i]: loop-independent dependence. Because b[i] is written in statement S2 in the ithe iteration, and also written in S3 in the same iteration.

Loop-carried dependences

Loop-carried dependence is defined as a dependence that exists between a statement in one iteration with another statement in a different iteration. Use the example code section above again to illustrate this definition.

• S1[i-1] ->T S2[i]: loop-carried dependence. Because a[i-1] is written in statement S1 in the (i-1)th iteration, and read in S2 in the next iteration.
• S3[i] ->A S4[i+1]: loop-carried dependence. Because c[i] is read in statement S3 in the ith iteration, which will be written in S4 in the next iteration.

DOALL

DOALL is the simplest kind of data parallelism, and in some special cases, could be the most efficient parallelism. In this kind of parallelism, all the parallel loop iterations are independent of one another and each of them is an individual parallel task. Let's use the example 3.1 in Solihin's Textbook to illustrate the DOALL parallelism.

for (i=1; i<n; i++)
    for (j=1; j<n; j++)
       S2: a[i][j] = b[i][j] + c[i][j];
       S3: b[i][j] = a[i][j-1] + d[i][j];

In this example, for i loop is the parallel loop. We could see that there is no loop-carried dependence across i iteration, which means that all iterations in the for i loop are independent with any other i iterations. This fact makes all the i iterations an individual parallel task and could be executed by individual processors at the same time.

In order to illustrate the execution of DOALL and give a better view of how it really works, we prune the inner loop that messes up our vision. The following is the simpler example:

for (i=1; i<n; i++)
       S2: a[i] = b[i] + c[i];
       S3: b[i] = a[i] + d[i];

Again, there is no loop-carried dependence across iterations, and all iterations are independent with any other iterations. The figure of execution of the iterations is shown as below:

To show the speedup obtained through the DOALL parallelism, we denote T_{S2}, T_{S3} as the execution time of statement S2, S3 respectively. It the loop is executed sequentially, the execution time is (n-1)(\(T_{S2}\)+T_{S3})

DOACROSS

In code 3.7, apparently there is a loop-carried dependence existing in the code.

S[i] -> T S[i+1]

Obviously, there is no way to implement it as DOALL parallelism.

Code 3.7 A loop with loop-carried dependence
for (i=1; i<=N; i++) {
 S: a[i] = a[i-1] + b[i] * c[i];}

If we split code 3.7 as two loops, then the fist loop can be implement in DOALL parallism. In code 3.8, first of all, we create a new array named temp[i]. Second, we put temp[i] in a loop which is individual and loop-independence. However, this solution generated a disadvantage: high storage. Due to increasing the array size of temp[i] by i++, the size of temp depends on the number of iterations instead of threads. If N ( # of iteration) is bigger, then the size of temp will be larger.

Code 3.8 A split version of the loop in Code 3.7
for (i=1; i<=N; i++) {  //this loop has DOALL parallelism
  S1: temp[i] = b[i] * c[i];}  
for (i=1; i<=N; i++) {
  S2: a[i] = a[i-1] + temp[i];}

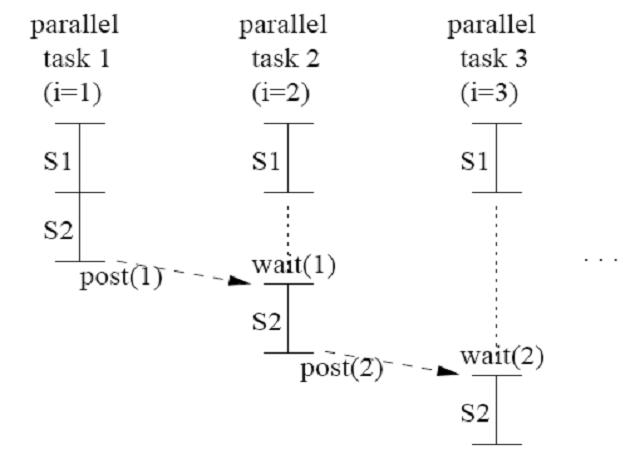
Let's see code 3.9, We still create a new array temp[i]. There are two differences between code 3.9 (DOACROSS) and code 3.8 (DOALL). First, the size of array is not increasing by the # of iterations but the # of threads, because temp[i] is not a shared array but a private scalar. Second, there is only one loop which contains S1 and S2. In DOACROSS parallelism, we insert two primitives, wait(name) and post(name). The principle of DOACROSS parallelism is to insert point-to-point synchronization. Notice the statement post(i) and and wait(i-1). post(i) is a signal produced by producer a[i]. Once a[i] has been produced, it will be post immediately. Meanwhile, the consumer is waiting i-1 by using wait(i-1). The reason makes consumer has to wait the previous a[i] is because S2 has to use a[i-1] to calculate to generate a[i]. Next, when S2 produce a[i], it will post it, post(i), to let the next consumer consume it. We will discuss how DOACROSS parallelism works in figure later.

Code 3.9 Exploiting DOACROSS parallelism in the loop from code 3.7
post(0);
for (i=1; i<=N; i++) {
  S1: temp[i] = b[i] * c[i];}
  wait(i-1);
  S2: a[i] = a[i-1] + temp[i];
  post(i);}

In this figure, we will introduce how DOACROSS parallelism executes by using post and wait. In task 1 (i=1), S2 post post(1) as it finishes its own statement. Next, in task 2 (i=2), when S1 finished its own statement, task 2 has to wait until task 1 finishes and post (1). The statement of S2 in task 2 is a[2] = a[2-1] + temp[2]; and it means S2 can not produce value without a[1]. The same to task 3, S2 in task 3 is a[3] = a[3-1] + temp[3]; and has to wait until task 2 finishes its task and post a[2].

DOPIPE

In code 3.12, there is a loop-carried dependence existing in the loop.

S1[i]-> T S1[i+1]

Code 3.12 A loop amenable to pipelined parallelism
for (i=1; i<=N; i++) {
 S1: a[i] = a[i-1] + b[i];
 S2: c[i] = c[i] + a[i];}

Here we split code 3.12 in 2 loops and make it parallelized in DOALL parallelism. For the first loop, there is no way to use DOALL parallelism because of loop-carried dependence. Otherwise, for the second loop, it is available to use DOALL parallelism since there is no loop carried dependence but loop-independence. Howevr, DOALL is not the only solution to parallelize code 3.12 and it still has an disadvantage. If there are only a few processors to run this program, then the speedup will not be too much. We will introduce another solution, DOPIPE parallelism, in code 3.13.

Code DOALL parallelism(transformed from 3.12) 
for (i=1; i<=N; i++) {  
  S1: a[i] = a[i-1] + b[i];}
for (i=1; i<=N; i++) { //this loop has DOALL parallelism
  S2: c[i] = c[i] + a[i];}

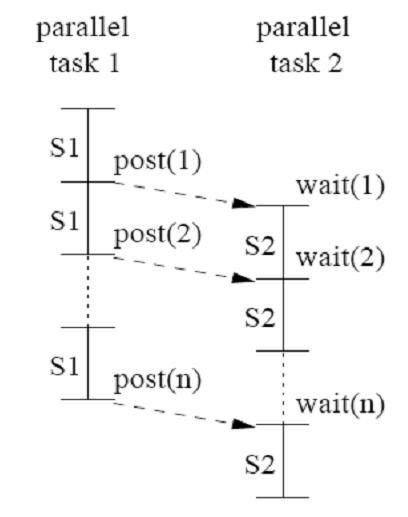
Here, we use DOPIPE parallelism to solve code 3.12. We still split code 3.12 as twp loops and insert primitive synchronization, post and wait. In order to calculate c[i], S2 has to get the value of a[i]. However, there is no a[i] in the second loop. S2 has to wait until S1 finished processing a[i] and post it. Once S1 produces a[i], S2 consumes a[i] immediately and starts process its own statement. We will explain this principle in figure later.

Code 3.13 DOPIPE parallel version of the loop from code 3.12
for (i=1; i<=N; i++) {  //this loop has DOALL parallelism
  S1: a[i] = a[i-1] + b[i];
  post(i);}
for (i=1; i<=N; i++) {
  wait(i);
  S2: c[i] = c[i] + a[i];}

This figure present us how DOPIPE parallelism works. Each task processes different statement. For example, task1 processes S1 and task2 processes S2 in this figure. On the other hands, S1 is a producer to produce a[i]. Once S1 produces a[i], it will post a[i], post(i), to let S2 consume. S2 has to wait for a[i] by using wait(i), because S2 does not know the value of a[i] until S1 produces and posts it.

References

1. wikipedia: Parallel Computing
2. FUNDAMENTALS OF PARALLEL COMPUTER ARCHITECTURE, Yan Solihin, Aug 2009