CSC/ECE 506 Spring 2010/ch 3 yl

Supplement to Chapter 3: Support for parallel-programming models. Discuss how DOACROSS, DOPIPE, DOALL, etc. are implemented in packages such as Posix threads, Intel Thread Building Blocks, OpenMP 2.0 and 3.0.

Parallel-programming models

Loop-independent vs. loop-carried dependences

Before performing the three kinds of parallelism analysis, we need to discuss about loop-dependence analysis first.

Statement dependences

To discuss code analysis, let's define the framework as follows. Let S denote a statement in the source code. Let [] denote loop iteration space. Let S1 -> S2 denote statement S1 executes before S2. Then, we further define three statement dependences:

• S1 ->T S2 denotes true dependence: S1 -> S2, and S1 writes to a location that is read by S2.
• S1 ->A S2 denotes anti dependence: S1 -> S2, and S1 reads a location written by S2.
• S1 ->O S2 denotes output dependence: S1 -> S2, and S1 writes to the same location written by S2.

To give a better understanding, we illustrate the dependences using the code section below:

for (i=1; i<N; i++)
  S1: a[i] = i;
  S2: b[i] = a[i];
  S3: b[i] = a[i]+c[i];
  S4: z[i] = 2*i;

DOALL

for    i:=2:N-1 do A(i):=[A(i-1) + A(i) + A(i+1)]/3; next i;
forall i:=2:N-1 do A(i):=[A(i-1) + A(i) + A(i+1)]/3;

for (i=2; i<=n; i+=2)
 s: a[i] = a[i-2];
for (i=3; i<=n; i+=2)
 s: a[i] = a[i-2];

DOACROSS

In code 3.7, apparently there is a loop-carried dependence existing in the code.

S[i] -> T S[i+1]

Obviously, there is no way to implement it as DOALL parallelism.

Code 3.7 A loop with loop-carried dependence
for (i=1; i<=N; i++) {
 S: a[i] = a[i-1] + b[i] * c[i];}

If we split code 3.7 as two loops, then the fist loop can be implement in DOALL parallism. In code 3.8, first of all, we created a new array named temp[i]. Second, we put temp[i] in a loop which is individual and loop-independence. However, this solution generated a disadvantage: high storage. Due to increasing the array size of temp by i++, the size of temp depends on the number of iterations instead of threads. If N ( # of iteration) is bigger, then the size of temp will be larger.

Code 3.8 A split version of the loop in Code 3.7
for (i=1; i<=N; i++) {  //this loop has DOALL parallelism
  S1: temp[i] = b[i] * c[i];}  
for (i=1; i<=N; i++) {
  S2: a[i] = a[i-1] + temp[i];}

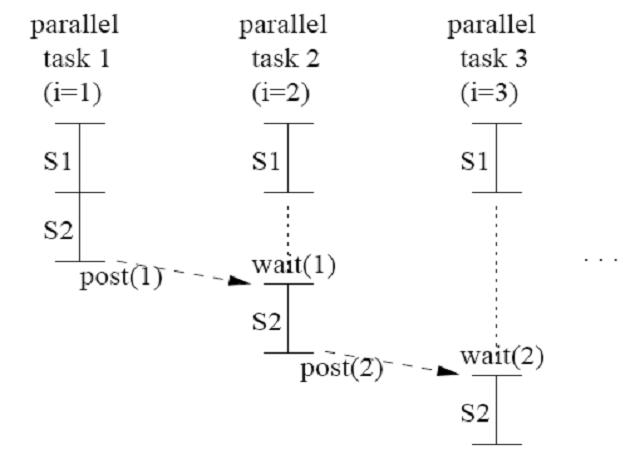
post(0);
for (i=1; i<=N; i++) {
  S1: temp[i] = b[i] * c[i];}
  wait(i-1);
  S2: a[i] = a[i-1] + temp[i];
  post(i);}

References

1. wikipedia: Parallel Computing
2. FUNDAMENTALS OF PARALLEL COMPUTER ARCHITECTURE, Yan Solihin, Aug 2009