CSC/ECE 506 Spring 2010/ch 3 yl

Supplement to Chapter 3: Support for parallel-programming models. Discuss how DOACROSS, DOPIPE, DOALL, etc. are implemented in packages such as Posix threads, Intel Thread Building Blocks, OpenMP 2.0 and 3.0.

Parallel-programming models

Loop-independent vs. loop-carried dependences

Before performing the three kinds of parallelism analysis, we need to discuss about loop-dependence analysis first.

Statement dependences

To discuss code analysis, let's define the framework as follows. Let S denote a statement in the source code. Let [] denote loop iteration space. Let S1 -> S2 denote statement S1 executes before S2. Then, we further define three statement dependences:

• S1 ->T S2 denotes true dependence: S1 -> S2, and S1 writes to a location that is read by S2. S1 is the producer of data that is read by the consumer (S2).
• S1 ->A S2 denotes anti dependence:

DOALL

for    i:=2:N-1 do A(i):=[A(i-1) + A(i) + A(i+1)]/3; next i;
forall i:=2:N-1 do A(i):=[A(i-1) + A(i) + A(i+1)]/3;

for (i=2; i<=n; i+=2)
 s: a[i] = a[i-2];
for (i=3; i<=n; i+=2)
 s: a[i] = a[i-2];

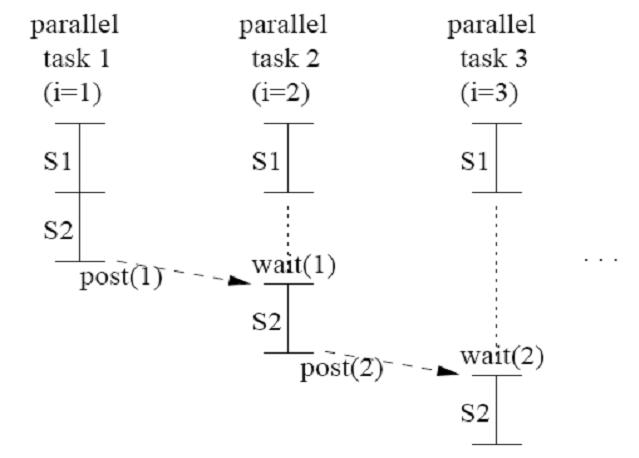
DOACROSS

for (i=1; i<=N; i++) {
 S: a[i] = a[i-1] + b[i] * c[i];}

for (i=1; i<=N; i++) {
  S1: temp[i] = b[i] * c[i];}
for (i=1; i<=N; i++) {
  S2: a[i] = a[i-1] + temp[i];}

post(0);
for (i=1; i<=N; i++) {
  S1: temp[i] = b[i] * c[i];}
  wait(i-1);
  S2: a[i] = a[i-1] + temp[i];
  post(i);}

References

1. wikipedia: Parallel Computing
2. FUNDAMENTALS OF PARALLEL COMPUTER ARCHITECTURE, Yan Solihin, Aug 2009