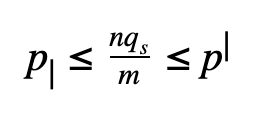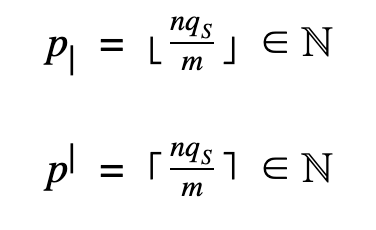CSC/ECE 517 Fall 2019 - E1986. Allow reviewers to bid on what to review

Why Should a Student bid for Reviewing Submissions?

If the choice of which submission to review is left to student itself, he/she would choose to review those topics which are related to their project or whatever they are highly interested in. This would benefit both the reviewer and reviewer because

From a Student's Perspective:

• Because he/she does not have to spend a lot of time understanding what is going on.
• The Student would be more focused on giving the review and hence judgment made tend to be more objective than subjective.
• This would improve the quality of reviews and will also be helpful for the reviewer.
• By implementing the color-coding feature, the student at any point knows which topic/s are more likely to get and he/she optimizes between "what they want" and "what they can get"
• Also, Bidding in Fun !!!!!!!

From the Instructor's Standpoint:

• Because opinions expressed in the reviews are a result of informed decisions, the inference made from the Machine Learning models trained on these data sets would make more sense.

Problem Statement

Currently Deployed Implementation

When an assignment participant wants to review others’ work, they will be asked to choose an assignment topic. The participant will be allowed to choose from among those assignment topics that have not been already assigned to 10 other participants. If they choose the ‘I do not care about the topic I review’ option, a random topic will be chosen from all the available topics and will be assigned to them. That is, the reviews are being allocated on a First Come First Serve basis.

Previous Work on this issue

E1856

E1928

What’s Deeply wrong in those implementations?

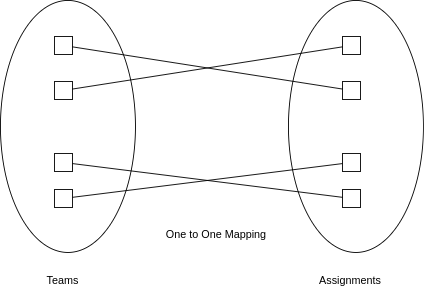
To understand what's wrong, first consider the differences between Teams Bidding for Assignments and Students Bidding for Reviews. Both of these are Matching or resource Allocation Problems.

The former can be modelled as a one-to-one matching problem. (i.e team and assignment has one-to-one correspondence).

However, Students and Reviews have many-to-many relationship (a student can choose multiple submissions for review and a submission can be given to multiple students for review)

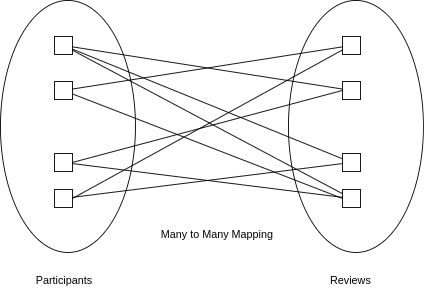
The Mathematical formulation is itself wrong in E1856 and E1928 and they have used the below shown diagram to represent the relationship.

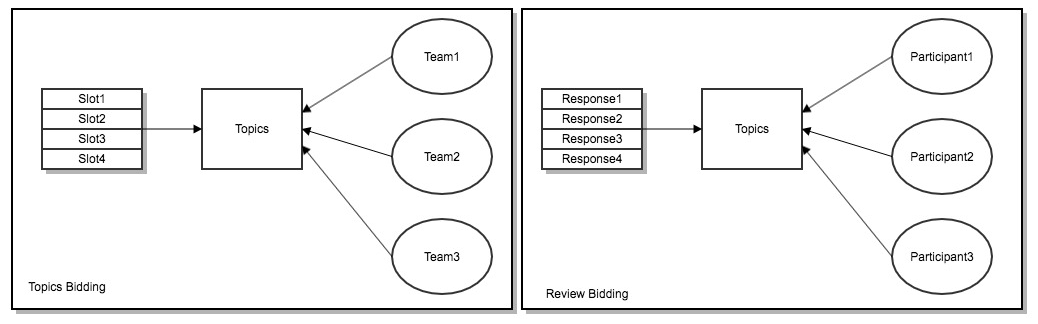
Why does the difference is the representation matter?

Since they have modeled the problem on the same lines, they have used the same version of the Gale-Shapley or Top Trading Cycles Algorithm used for one-to-many or one-to-one approach. Famous Problems Dealt on these lines.

Stable Marriage Problem (One-to-One)

School Choice Problem (One-to-Many)

Other Implementation pitfalls observed

E1928

• Once the bidding for review topics is done, the selections need to be saved to the database which is not happening and when the page is refreshed, the UI does not retain the bids.
• The button responsible for running the algorithm cannot be checked and it is a hunk-like icon.
• The button appears multiple times on the page.
• The algorithm needs to be implemented in the web service which should be ideally be used from the lottery controller which is not they have tried to implement. The entire code is written in Ruby.
• The algorithm needs to skip the review topic that the user has worked on. This Code already exists for topic and again written in the new implementation that needs to be integrated into the existing one and hence needs refactoring.
• Proper tests need to be written.

What needs to be done?

The participants should be able to bid for topics to review in the same way they bid for topics to work on.

Approach for matching students with topics

We have a set of students S = {S₁, ..., S_n}, and a set of topics T = {T₁, ..., T_m}. Each student must get exactly q_S topics (The threshold in our case is q_S = 4, it’s up to the student to decide how many of these they want to actually review.), while each topic must be assigned to at least q_T reviewers. Students will submit a list of preferences over the set of topics in linear order. If they submit the preferences for only a certain topics, the rest of the topics will be appended to their preference list in a random order. The topics shall have (possibly different) linear order preference over the set of students according to the timestamps of their time of bid and the total number of topics they have bid for. Students with lower timestamps and who bid for lower number of topics will be given higher preference.

To begin, we will try to obtain a matching with an approximately equal number of students reviewing each topic, which we call uniform distribution. If no uniform stable matching exists, our mechanism will nonetheless return a stable matching, provided one exists for a given profile of preferences.

The average number of reviewers assigned to each course will be

where n is the number of students, and m is the number of courses.

Clearly, this number is not necessarily an integer. Let us assume that

where

Matching 𝝁 is a mapping which assigns exactly qS different topics to each student in Sand at least qT different students to each topic in T. We denote the set of topics assigned by matching 𝜇 to the student si and the set of students who were assigned the topic tj as 𝜇(si) and 𝜇(tj),respectively.

Blocking Pair (Defined according to our problem): A pair (s, t) is called a blocking pair, if the student is associated with the topic (If he/she is in the group which works on topic t). A Matching Set M is considered Stable if it does not have any blocking pairs.

The matching is (pairwise) stable if there are no blocking pairs.

Mechanism:

First we calculate k, p|, and p|. The goal is for each topic to be assigned to either p| and p| students, and to assign exactly qS courses.

The algorithm:

Step 1: Each topic proposes to accept the first pI students in its preference list. Each student accepts no more than qS proposals according to his/her preferences, rejecting the rest. Step k: Each course that has z < pI students proposes to accept pI - z students it has not yet proposed to. Each student accepts no more than qS proposals according to his/her preferences, rejecting the others.

The algorithm stops when every topic that has not reached the maximum quota pI has proposed acceptance to every student.

Functional Requirements

• Each participant should be able to submit a list of preferences in decreasing preference order for the topics they would like to review. The list may contain any number of topics.
• During bidding, the topics should be color-coded according to the number of participants who are contending for each topic. The colors should range from green to red with green representing a topic with a low number of bids and red representing a topic with a high number of bids.
• There should be a deadline before which all participants must submit their list of preferences.
• After the deadline, the course instructor should be able to run the bidding algorithm after which each participant will be assigned a list of topics to review. The number of topics assigned to a participant should be minimum(4,k) where ‘k’ is the number of topics in their preference list.
• Once the topics to review have been assigned, the participants should be able to see those topics they have been assigned and give feedback to the submission for each topic.
• If a participant has given feedback to less than 4 topics and chooses to review a submission, the topic with the minimum number of current reviewers will be assigned to that participant.

Non-functional Requirements

• There must exist a web service that takes the participants and their respective preference lists as input runs a bidding algorithm like top trading cycles and returns a map of the participants and the list of topics assigned to each participant.
• This web service must either be called from the LotteryController or a new controller can be created on the same (if Lottery Controller becomes too complex).

Implementing the Web Service

• 1) Python
• 2) Flask (Minimal MVC Framework for Python Backend)
• 3) JSON as the Data Serialization Format.
• 4) Deployment (AWS or VCL)
• 5) Apache Web Server or GUnicorn or Default Flask Server.

(Potential) Addition/Modification of files in expertiza

• 1) Lottery Controller
• 2) Review Mapping Controller
• 3) A New model to store the bidding information entered by the student.
• 4) Unit Test Files Associated
• 5) Views/Routes Associated

Test Plan

• Ensuring that the algorithm results in stable matchings. The concept of stability is defined above.
• Check whether the UI reflects the bids made by the user.
• Testing that the color-coding feature is working and appropriate.
• Check if a user is assigned 4 topics for review, even though he might have bid for any number of topics.
• Regression testing if the code is added in the lottery controller. If new model/controller is added then relevant tests will be included based on the proposal acceptance.
• Tests to ensure that each review topic gets minimum number of reviews.
• Tests to check whether the web service works as expected.

Project Mentor

Ramya Vijayakumar (rvijaya4@ncsu.edu)

Team Members

Yaswanth Soodini (ysoodin@ncsu.edu)

Sai Shruthi Madhuri Kara (skara2@ncsu.edu)

Ayushi Rungta (arungta@ncsu.edu)

Vivek Karri (vkarri@ncsu.edu)

Important references

InteligentAssignment

Many-to-Many-Matching-Problem-with-Quotas-by-Freer-and-Titova

Project_E1928._Allow_reviewers_to_bid_on_what_to_review

E1856_Allow_reviewers_to_bid_on_what_to_review