CSC/ECE 506 Spring 2015/7a ap

Previous Page: http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2013/7a_bs

Current Page: http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2015/7a_ap

Memory Consistency

Memory consistency deals with the ordering of all memory operations/accesses (loads and stores) to different memory locations. It can be summarized as the rule which must be enforced among all loads and stores to different locations in a shared memory by different processors. It can also be present in systems without caches.

Memory Consistency Model

In order to maintain memory consistency in a multiprocessor system when a program is executed on it, a model is required to specify the behavior of how the memory has to be accessed or to provide an agreement between the memory implementation and the program which is going to utilize this memory. This model is called Memory Consistency Model and It is used to define the ordering in which all loads and stores must be performed, both relative to each other in the same program and to other loads and stores by another program on another processor. The programmer before writing the code must have knowledge of the Memory Consistency Model used by the hardware in order to ensure program correctness. The code below from Solihin<ref>Yan Solihin. "Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems." Solihin Publishing & Consulting LLC, 2009.</ref> shows an example of possible inconsistency:

                      P0                                          P1
                S1 : datum = 5                            S3 : while(!datumIsReady) {}
                S2 : datumIsReady = 1                     S4 : print datum

In this example, P0 generates sets the values of datum and datumIsReady. By setting datumIsReady to 1, this signals P1 that datum is now ready. P1 spins in the while loop waiting for this flag to become 1 and then prints datum. In this example an in similar cases, it is important that the compiler understand what the programmer intended so that the program order is preserved. Within a uni-processor, this problem can be solved by declaring which variables must be synchronized. For instance when using C, this can be accomplished by declaring variables that may be susceptible to inconsistency as volatile.

When a programmer writes a code, then he implicitly expects that the order of all memory accesses (loads and stores ) coming out of a pocessor will be performed in the program order and each memory access will be performed atomically. The code below from Solihin<ref>Yan Solihin. "Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems." Solihin Publishing & Consulting LLC, 2009.</ref> shows another example of possible inconsistency:

                      P0                                        P1                                       P3
                S1 : x = 5                            S3 : while(!xReady) {}                        S6: while(!xyReady)
                S2 : xReady = 1                       S4 : y = x + 4                                S7: z = x * y
                                                      xyReady = 1

Example 2

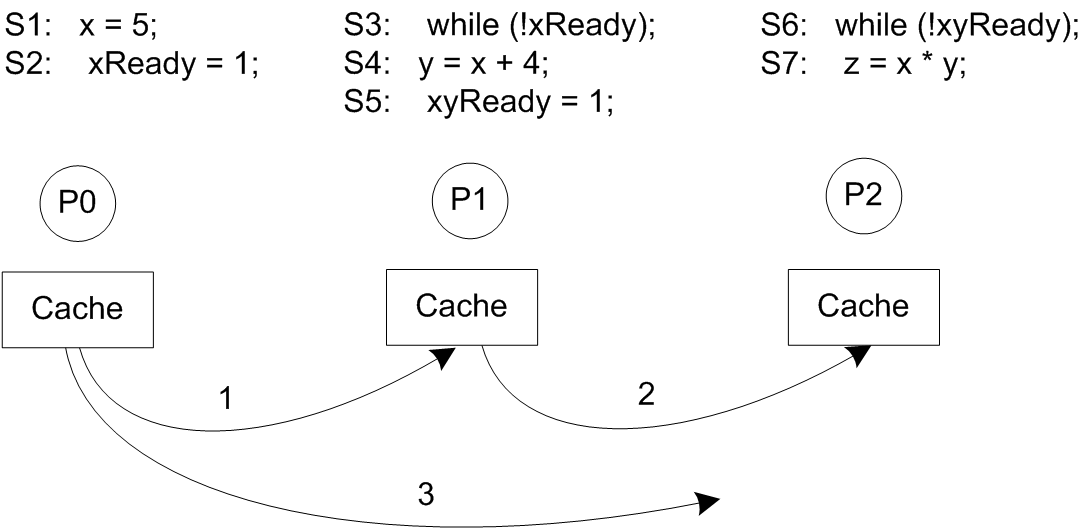
In the above example, initially, the values of x, y, z, xReady and xyReady are zero. If we consider that the program order to S1 S2 S3 S4 S5 S6 S7.

So as per the code, firstly P0 executes its statements S1 and S2 in order and sets the value of x as 5 and then xReady as 1. After that, P1 executes its statements in order of S3 then S4 then S5. P1 reads the value of xReady and comes out of the loop and then reads the value of latest x (which is 5) to calculate the value of y. Once it is calculated then the variable xyReady is set to 1. P3 then checks the value of the variable xyReady and comes out of the loop. Then it reads the latest value of x and y (which is 5 and 9) and find the value of z. The programmer expects that the value of z should be 45 (5*9) due to the atomicity of the execution of the instructions.

Now, consider the following scenario. P0 executes S1, which writes a value of 5 to x. This write is then propagated to P1 and P2, however it reaches P1 faster that P2. Then, P0 performs a write to xReady, which is also propagated to P1. P1 now sees the new values of xReady and x. So P1 excutes its S4 statement, assigning a value of 9 to y, and then sets xyReady to 1which is propagated to P2. P2 then gets out of its loop and reads the value of x and y. Since the value of x from P0 has yet not reached P2, P2 reads a fresh value of y but the stale value of x. Thus the output of the program is un-expected which in this case is z = 0.

INSERT PICTURE HERE

From the first and second example we can understand that the implicit expectation of the programmer is:

1) Memmory accesses performed by a single processor should be occured in program order and

2) Each of them should be performed atomically.

Such an expectation was formally defined as the Sequential Consistency which we are going to Describe first.

Memory Semantics in Uniprocessor Systems

Uniprocessor languages use simple sequential semantics for memory operations, which allow the programmer to assume that all memory operations will occur one at a time in the sequential order specified by the program. Thus, the programmer can expect a read to return the value of the most recent write to the location according to sequential program order. It is sufficient to only maintain uniprocessor data and control dependences. The compiler and hardware can freely reorder operations to different locations if the uniprocessor data and control dependences are respected. This enables compiler optimizations such as register allocation, code motion, and loop transformations, and hardware optimizations, such as pipelining, multiple issue, write buffer bypassing and forwarding, and lockup-free caches, all of which lead to overlapping and reordering of memory operations.<ref>Sarita V. Adve. Kourosh Gharachorloo. "Shared Memory. Consistency Models: A Tutorial." Digital Western Research Laboratory 250 University Avenue Palo Alto. <http://www.hpl.hp.com/techreports/Compaq-DEC/WRL-95-7.pdf</ref>

Memory Semantics in Multiprocessor Systems

Unfortunately, memory consistency is not as straight-forward on multiprocessors. With regard to the example above, instead of each process running on a separate thread, each process runs on a separate processor. With multiple processors, more problems arise with respect to order of execution. While one process might execute instructions in program order, other processes may not recognize the executions in the same order due to delays in communication. How processors handle this problem depends on the chosen consistency model<ref>http://www-vs.informatik.uni-ulm.de/teach/ss05/dsm/arizona.pdf</ref>.

Types of Memory Consistency Models

INSERT MCM_TREE HERE

Tree

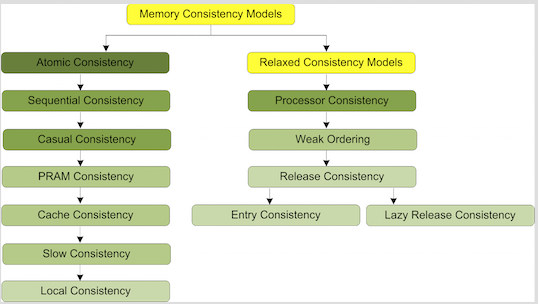
The tree represents most of the memory consistency models. There are some other memory consistency models as well. These are:

1) Delta Consistency Model

2) Entry Consistency Model

3) Eventual Consistency Model

4) Fork Consistency Model

5) One-Copy Serializability

6) Vector-Field Consistency Model

Following are the detailed explanation of consistency models<ref>http://en.wikipedia.org/wiki/Consistency_model</ref>:

Atomic or Strict Consistency

<ref>http://en.wikipedia.org/wiki/Linearizability</ref> This model is the strictest of all consistency models. The model works on the concept of atomicity. In this model, all the memory accesses are performed atomically that is one memory access from any one processor can be executed at any given time and secondly the whole sequence of memory accesses are executed entirely. They can not be interrupted by any concurrent operation. Due to very high restrictions on memory operations, this model has low performance.

Sequential Consistency

<ref>http://en.wikipedia.org/wiki/Sequential_consistency</ref> The most commonly assumed memory consistency model for shared memory multiprocessors is Sequential Consistency Model. This model is similar to Atomic Consistency but it contains the possiblity of optimizations to improve the performance. Sequential Consistency was formally defined by Lamport as follows:

“A multiprocessor system is sequentially consistent if the result of any execution is the same as if the operations of all the processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by its program.”

There are two main aspects to sequential consistency:

(1) Maintenance of the program order among memory operations from individual processors

(2) Maintenance of a single sequential order among memory operations from all processors

The second aspect makes it appear as if one memory operation executes atomically or instantaneouslywith respect to other memory operations.

INSERT IMAGE HERE

Basic Implementation of Sequential Consistency

The basic implementation of SC involves execution of one memory access at a time without overlapping it with another memory access. Thus it is required to understand the starting and ending point of a particular memory access. Memory accesses are performed when either there is a load or a store operation: Let us consider a load operation,

Step 1- computation of effective address in a functional unit.

Step 2- cache access to the effective address issued by memory hierarchy.

Step 3- fetching the data value associated with the address.

Step 4- returning the value to the destination register of the load instruction.

Here, it is clear that step 1 and step 4 are not affected by other memory accesses. Effective address is computed in the functional unit which involves computation not access. Similarly the final value to be loaded in the destination register has already been fetched from the cache so it does not invlove any further memory access. Thus it can be concluded that the actual load (which involves memory access) starts from step 2 and ends on step 3. These two steps should be performed atomically.

Let us consider store operations:

Step 1- computation of effective address in a functional unit.

Step 2- the store is consigned by copying the destination address and the latest value to be written to a write buffer.

Step 3- the store value in the write buffer is released to the cache.

Step 4- the store is considered complete only when this new value is fully propagated to the other processors.

As the store invloves multiple cache values thus effectively the store starts when the destination address is issued and the latest value is stored in the write buffer in step 2 till the step 4 where the store is fully propagated to other caches. So these steps should be performed atomically. It can be concluded that the basic implementation of SC inflicts a lot of restriction on how the intructions within a program have to executed and thus it affects the performance. So in order to improve the performance of SC, few optimizations in the model are possible . INSERT IMAGE HERE

Techniques to improve Sequential Consistency Performance

It can be concluded that the performance of an SC implementation can be improved if the execution of memory accesses is made faster and when it is allowed for the memory accesses to be overlapped with respect to one another.

1) The first performance enhancement technique avoids the overlapping of execution of loads and stores but involves overlapping of the data fetches that are generated by these loads and stores.

2) The second technique of performance enhancement depends on speculation access where the execution of a load can be overlapped with the execution of the older load by speculatively assuming that the older load is executed atomically. If the older load doesnot get executed atomically then this younger load is canceled and then it is executed again. This speculative execution is typically only implemented for loads. All stores are issued to the cache atomically only.

Causal Consistency

<ref>http://en.wikipedia.org/wiki/Causal_consistency</ref> Casual Consistency Model is a weaker Model of Sequential Consistency Model. Here, a differentiation is made between events that are potentially causally connected with each other and those that are not. A system provides Causal Consistency if memory operations that potentially are causally related are seen by every processor of the system in the same order. Operations that are not causally related are said to be concurrent. Concurrent writes (i.e. ones that are not causally related) may be seen in different order by different processors but Condition-writes (i.e. ones that are potentially causally related) must be seen by all processes in the same order.

When a store operation follows a load operation performed by a processor then the load and store are considered casually connected. Similarly, when a load operations follows a store operation then it is also considered casually connected. Also, even two stores operations performed by the same processor are defined to be causally ordered, in the order they were performed.

INSERT IMAGE HERE

Here, load operation r3(x) is casually dependent on store w2(x) and load operation r4(x) is casually dependent on store w1(x).

PRAM Consistency

<ref>http://en.wikipedia.org/wiki/PRAM_consistency</ref> PRAM consistency is pipelined random access memory consistency. It is also known as FIFO consistency. This consistency model is even more relaxed than casual consistency model. In this consistency model, all processors see the stores performed by one processor in the same order as they were issued from that processor. But stores performed by different processers may be seen in a different order by different processors. In this consistency model, only the store order needs to be consistent not the load and that is why it is named as pipelined. PRAM consistency is easy to implement. The model simply says that there are no guarantees about the order in which different processors see the stores, except that two or more stores performed by the single processor must arrive in order, as if they were in a pipeline.

INSERT IMAGE HERE

Cache Consistency Model

Cache Consistency is dealt using cache coherence protocols. This model simply requires that all store operations to the same memory location by the processors are performed in some sequential order. Also, the apearance of their order to other processors is same as the order in which they are performed.

Slow Consistency Model

The Slow Consistency Model is weaker than PRAM Consistency Model. This model states that when a load operation is performed on a memory location then the memory returns the latest write operation performed on it. But succeeding loads to the same location may not return stores issued earlier (by the processor that issued the earlier stores) than the first load.

INSERT IMAGE HERE

Local Consistency Model

Local Consistency Model is considered to be the weakest model. The model requires that all the load and store operations by the performed by a processor are apeared to that processor as if they are performed on a single processor system. Although, there is no restriction on how the order of memory operations performed by different processors will apear to different processors.

Relaxed Consistency Models

These models basically loosen up the memory access restrictions of Sequential Consistency model. As these models do not put a lot of restriction on the sequence of the memory access thus their performance is better than Sequential Consistency Model. But the implementation of these models require a lot of complexity in the program. During coding, the programmers have to make sure that their programs obey the rules of the consistency model that the hardware provides.

Relaxation in the memory accesses may allow the order of execution of the instructions in a program different from the programmer’s expectation. Thus to prevent any non-deterministic outcome of the program, safty net is provided to the programmers to implement it in their program to specify strict ordering between a pair of memory accesses. This safty net is provided in terms of fence instruction. Once a fence instruction is implemented in the program then it prohibits all the memory accesses following it until all the memory accesses before it have been completed. Fence instruction is of two types. When the fence is only applied to the stores such that there is a proper ordering of the memory accesses between all the stores before the fence and all following it then such type of fence is called store fence/barrier. On the other side, when the fence is only applied to the loads such that there should be perfect ordering between the loads before the fence apears and the loads after the fence then such a fence is called load fence/barrier.

When a fence is implemented in the program then all the memory accesses younger than fence are flushed out from the pipeline. Firstly all the memory accesses older than fence are completed. After that the processor state is restored to the state prior to the fence instruction and execution is resumed from that point.

Processor Consistency Model

In Sequential Consistency, on all the memory accesses, a proper ordering is forced that is Load -> Load, Load -> Store, Store -> Store, and Store -> Load. The basic implementation of a Processor Consistency Model is based on relaxing the ordering between an older store and a younger store (Store -> Load). In this model, when a store has not completed, a younger load is allowed to issue to the cache and even complete. The importance of this is that store instructions can be queued in the write buffer and be completed at a later time without the use of load speculation. In the mean time, loads do not require to wait for the older stores to complete and can access the cache and hence they reduce the load latency. In case of PC, when a load is issued to the chache then it is not rolled back even if the illusion of atomicity is broken in contrast to SC where the load is rolled back at once. This result is better performance of PC as compared to SC. PC only relaxes one ordering rule out of four, hence it only affects the correctness of code that has a store followed by a load. If a program is properly synchronized programs, PC provides the same outcome as SC. In a post and wait synchronization in which a processor produces a data value and sets a flag to signal tha availability of the new value. This involves at least two store instructions, which are ordered with respect to each other in PC. Once the comsumer sees the flag high the it performs at least two loads and this ordering is also gurenteed under PC. Thus, post and wait sysnc produces te same outcome in PC as in SC.

INSERT IMAGE HERE

Weak Ordering Model

<ref>http://en.wikipedia.org/wiki/Weak_consistency</ref> When a programmer writes a program then he makes sure that the ordering issue is addressed using synchronization primitives. So it could be said that a majority of the programs are properly synchronized. These synchronization primitives can be of the form of barriers, point-to-point synchrnozation, lock etc. Also it can be concluded that if a program is properly synchrnonized , there is no data race that can occur. Data race is defined as simultaneous accesss of a single locations by multiple threads in which at least one of the access is a store. Simulatanous loads do not chance the outcome of the loads hence they cannot produce data race. Simulatanous stores may overwirte each other hence they can induce data race. A simulatanoues load and store also may cause the load to return different values. The implication of the lack of data race in a properly synchronizaed program is that the ordering of memory accesses can be relaxed except at synchronization points. This concept is implemented in Weak Ordering Consistency Model. The WO model uses 2 assumptions:

1) Programs are properly synchronized and

2) Programmers correctly express to the hardware which loads and stores act as syncrhonization accesses.

Based on the assumptions, we can define the correct behaviour of a synchronization access:

1) Before a synchronization access can issue, all prior loads, stores and synchronization accesses must have completed and

2) All loads, stores. And synchronization accesses following it must not have issued.

Basic Implementation of Weak Ordering Model

When a synchronization access is encountered at the processor pipeline, first of all, all the memory accesses following this synchronization point are flushed out of the processor pipeline. Then this synchronization accees itself is made to halt until all the memory accesses before this synchronization point are completed. All the loads have obtained their value and all the stores have been propagated their values. WO is more relaxed than PC because a WO compiler can re-order the memory accesses and it just have to make sure that they do not cross the synchronization point. In PC only Store Load access is relaxed. WO works well if the critical section is big containing more memory accesses to be executed. If the critical section is small then there is very less opportunities to reorder the memory accesses as there are less number of them. So when critical section is small then PC outperforms WO. WO is more relaxed but when program complexity is concerned then PC is better than WO.

INSERT IMAGE HERE

INSERT CODE HERE

Release Consistency Model

<ref>http://en.wikipedia.org/wiki/Release_consistency</ref> The Release Consistency model implementation is based on two different types of syncrhonization accesses:

Acquire syncrhonization (lock): which ensures that no younger load/store executes before the acquire is complete. Thus it prevents upward migration of memory accesses but not downward migration.

Release syncronization (unlock): which ensures that all older loads/stores complete before the release is issued. This it prevents downward migration of memory accesses but no upward migration.

It is also made sure in this model that acquires and releases must execute atomically with respect to one another. This implies that they must not appear to have overlapped their execution with respect of one another. This model requires all syncronization accesses in a program to be indetified correctly and completely, so that the hardware can ensure correct execution of properly synchronized program. Programming complexity is higher in RC than in WO.

Basic Implementation of Release Consistency Model

The release synchronization must prevent downward migration, so when a release synchronization access is encountered in the processor pipeline, the release access is halted until all prior memory accesses have completed. An acquire syncrhonization must prevent upward migration. When an acquire synchronization access is encountered in the processor pipeline, all instructions younger than it (including all loads and stores) are cancled and re-executed after the acquire syncrhonization completes. Similar to WO, RC allows the compiler to freely recorder loads and stores excep that they cannot migratre upward past as acquire synchronization and cannot migrate downward past a release synchronization . However, this flexibility and perfornamce advantage of RC results in higher complexity of the program.

INSERT IMAGE HERE

INSERT IMAGE HERE

Lazy Release Consistency Model

The Lazy Release Consistency model is a further optimization of the Release Consistency model (RC) in which it is considered that the thread that executes an acquire synchronization does not need values written by another thread until the acquire synchronization is completed. When a store is executed in a critical section then before the unlock is executed it is made sure that the this memory access is propagated fully to the other caches. Then the unlock operation is executed which involves another store where the value of lockvar is changed to 0. This value is again propagated fully to other caches and then after that the lock operation is executed. It can be concluded that the value of the store in the first critical section is not required until the lock operation for the second critical section is executed. So it can be said that the propagation of the values written prior to the release synchronization can be delayed until the release synchronization is complete and then both the values wiritten in the critical section and on release synchronization can be propagated togather to the other caches. This model is beneficial in the cases where there is a little bandwidth available between the processors or in a system where there are high overheads due to the propagation of small amount of data or infrequent propagattion of large amount of data.

INSERT IMAGE HERE

Other Consistency Models

Delta Consistency Model

<ref>http://en.wikipedia.org/wiki/Delta_consistency</ref> This model is a core functionality that gives content providers “freshness guarantee” by ensuring that updates will propagate through the system and all replicas will be consistent after a fixed time period.

Entry Consistency Model

<ref>http://en.wikipedia.org/wiki/Entry_consistency</ref> This model requires the programmer to use acquire and release at the start and end of each critical section, respectively. Entry consistency requires each ordinary shared variable to be associated with some synchronization variable such as a lock or barrier. If it is desired that elements of an array be accessed independently in parallel, then different array elements must be associated with different locks.

Eventual Consistency Model

<ref>http://en.wikipedia.org/wiki/Eventual_consistency</ref> This model states that given a sufficiently long period of time over which no changes are sent, all updates can be expected to propagate eventually through the system and the replicas will be consistent.

Fork Consistency Model

<ref>http://en.wikipedia.org/wiki/Fork_consistency</ref> In this model, if an untrusted server hides the modifications of one writer to another, the latter will not be shown any future modifications of the former, effectively forking the views of them. This is the strongest consistency model that can be achieved with an untrusted server.

One-Copy Consistency Model

<ref>http://en.wikipedia.org/wiki/One-copy_serializability</ref> This model is the same as sequential consistency, as though there is only one copy of the file, thus, access requests are fully serialized.

One-Copy Consistency Model

<ref>http://en.wikipedia.org/wiki/One-copy_serializability</ref> This model is the same as sequential consistency, as though there is only one copy of the file, thus, access requests are fully serialized.

Vector-Field Consistency Model

<ref>http://en.wikipedia.org/wiki/Vector-field_consistency</ref> This is a consistency model for replicated data. It is designed to allow bounded divergence of object replicas. In this model replica consistency is selectively and dynamically strengthened or weakened based on the on-going game state and simultaneously it manages: how the consistency degree is changed throughout the execution; and how the consistency requirements are specified.

References

<References> [1] Yan Solihin. "Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems." Solihin Publishing & Consulting LLC, 2009.

[2] Sarita V. Adve. Kourosh Gharachorloo. "Shared Memory. Consistency Models: A Tutorial." Digital Western Research Laboratory 250 University Avenue Palo Alto. <http://www.hpl.hp.com/techreports/Compaq-DEC/WRL-95-7.pdf>

[3] Kai Li, and Paul Hudak. "Memory coherence in shared virtual memory systems". Published in Journal ACM Transactions on Computer Systems (TOCS), Volume 7 Issue 4, Nov. 1989 <http://dl.acm.org.prox.lib.ncsu.edu/citation.cfm?id=75104.75105&coll=DL&dl=GUIDE&CFID=251927&CFTOKEN=71004880>.

</References>

Quiz

2.What is the major difference between One copy Serializabilty and Sequential consistency?

a) No difference

b) One copy Serializabilty Model has only one copy of the file.

c) Sequential Consistency Model has only one copy of the file.

d) None.

4.On what basis are memory consistency strategies classified? (More than one options could be correct)

a) Page faults

b) Page synchronization

c) Page ownership

d) None.

6.Which of the following is true about sequential consistency? (More than one options could be correct)

a) All orderings are enforced.

b) Loads and stores can exchange positions freely.

c) Performance can suffer

d) SC is deterministic

Quiz Answers: 1. b,c 2. b 3. c 4. b,c 5. b 6. a,c 7. c 8. a,d