CSC/ECE 506 Spring 2013/12a TS

Interconnection Network Architecture

In a multi-processor system, processors need to communicate with each other and access each other's resources. In order to route data and messages between processors, an interconnection architecture is needed.

Typically, in a multiprocessor system, message passed between processors are frequent and short¹. Therefore, the interconnection network architecture must handle messages quickly by having low latency, and must handle several messages at a time and have high bandwidth.

In a network, a processor along with its cache and memory is considered a node. The physical wires that connect between them is called a link. The device that routes messages between nodes is called a router. The shape of the network, such as the number of links and routers, is called the network topology.

History of Network Topologies

The use of different topologies has changed over the years. The following pie charts from top500.org show the share of different network topologies over the years.

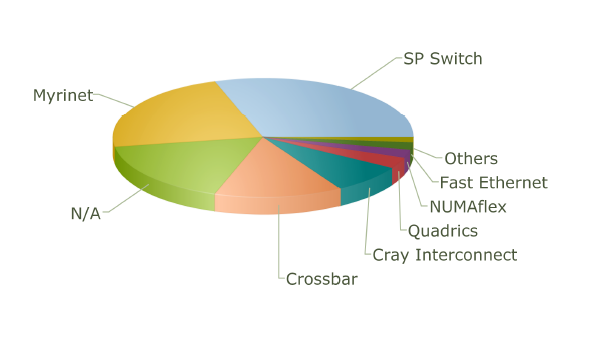Interconnect Family Market Share for 2001 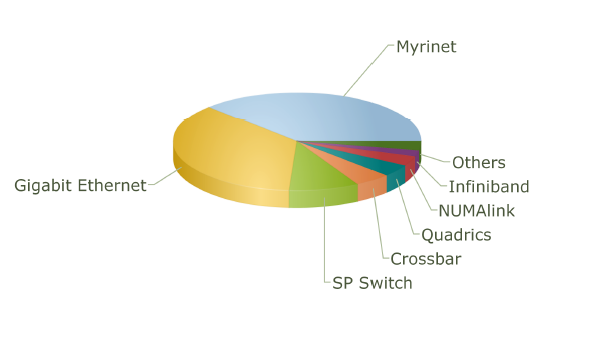Interconnect Family Market Share for 2004 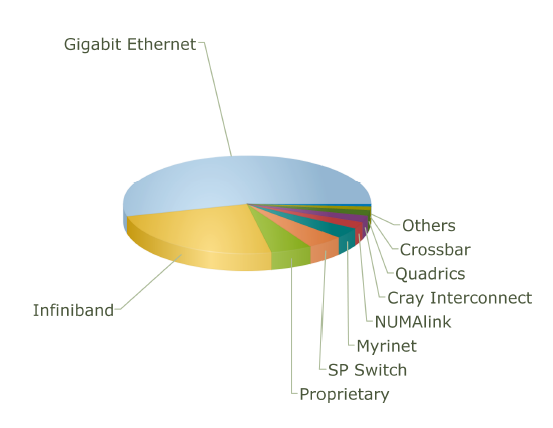Interconnect Family Market Share for 2007 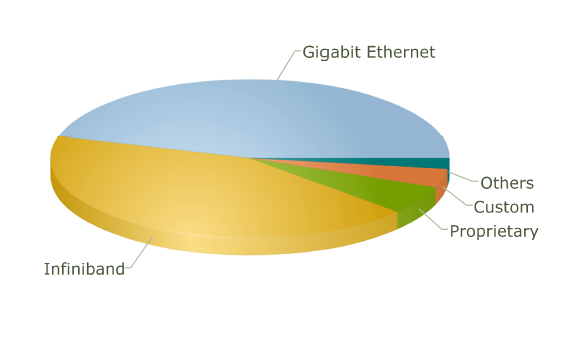Interconnect Family Market Share for 2010

Performance Metrics for Interconnection Network Topologies

The several metrics used for evaluating characteristics of a network topology like latency, bandwidth, cost, etc. are as follows:

• Diameter: This is the longest distance between any pair of nodes of the network. It is measured in terms of network hops (the number of links the message must travel before reaching the destination).
• Bisection Bandwidth: This is the minimum number of links that one must cut in order to partition the network into two halves.
• Degree: This is the total number of links in and out from a router.

The Diameter and Bisection bandwidth are the measure of performance of a network while the degree along with the total number of links is the measure of cost.

Interconnection evolution in the Top500 List

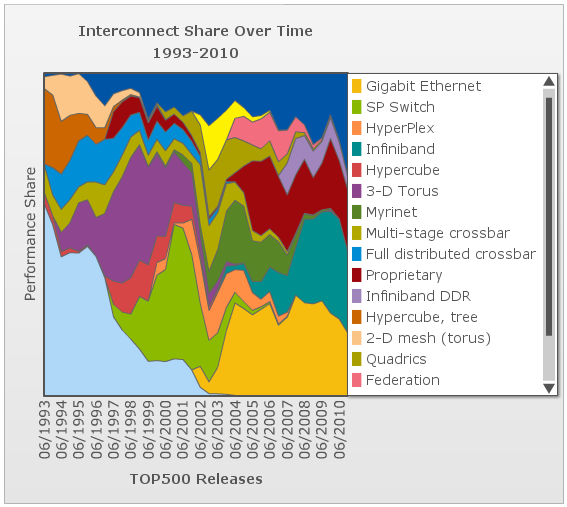
This chart shows the evolution over time of the different interconnect topologies by their dominance in the top500 list of supercomputers ⁷. As one can see, many technologies came into vogue briefly before losing performance share and disappearing. In the early days of the list, most of the computers list that the interconnect type is not applicable. However, the trailing end of the hypercube phase is clear in burnt orange. The dark blue at the top is "other" and the dark red in the middle is "proprietary", so we can only speculate about what topologies they might employ. The toroidal mesh appears briefly at the start in a cream color, and slightly outlasts the hypercube. The two crossbar technologies (blue and olive) followed the toroidal mesh. The fully-distributed crossbar died out quickly, but the multi-stage crossbar lasted longer but wasn't ever dominant. The 3-D torus (purple) dominates much of the 90s with hypercube topologies (dark pink) enjoying a short comeback in the later part of the decade. SP Switch (light olive), an IBM interconnect technology which uses a multi-stage crossbar switch replaced the 3-D torus⁸. Myrinet, Quadrics, and Federation all shared the spotlight in the mid 00s each used a similar fat-tree topology^9,10. The current class of supercomputers is dominated by nodes connected with either Infiniband or gigabit ethernet. Both can be connected in either a fat-tree or 2-D mesh topology. The primary difference between them is speed. Infiniband is considerably faster per link and allows links to be ganged into groups of 4 or 12. Gigabit ethernet is vastly less expensive, however, and some supercomputer designers have apparently chosen to save money on the interconnect technology in order to allow the use of faster nodes ^11,12.

Types of Network Topologies

Several metrics are normally choose to represent the cost and performance for a certain topology. In this section, degree, number of links, diameter and bisection width will be calculated for each topology.

Linear Array

The nodes are connected linearly as in an array. This type of topology is simple, however, it does not scale well.

• Diameter: p-1
• Bisection BW: 1
• # Links: p-1
• Degree: 2

A linear array is the cheapest way to connect a group of nodes together. The number of links and degree of linear array have the smallest value of any topology. However, the draw back of this topology is also obvious: the two end points suffer the longest distance between each other, which makes the diameter p-1. This topology is also not reliable since the bisection bandwidth is 1.

Ring

Similar structure as the linear array, except, the ending nodes connect to each other, establishing a circular structure.

• Diameter: p/2
• Bisection BW: 2
• # Links: p
• Degree: 2

Compared with the cheapest linear array topology, the ring topology uses least effort (only add one link) to get a relatively big improvement. The longest distance between two nodes is cut into half. And the biseciton bandwidth has increased to 2.

2-D Mesh

The 2-D mesh can be thought of as several linear arrays put together to form a 2-dimensional structure. This topology is very suitable for some of the applications such as the ocean application and matrix calculation.

• Diameter: 2(sqrt(p)-1)
• Bisection BW: sqrt(p)
• # Links: 2sqrt(p)(sqrt(p)-1)
• Degree: 4

Nodes that are not on the edge have a degree of 4. To calculate the number of links, add the number of vertical links, sqrt(p)(sqrt(p)-1), to the number of horizontal links, also sqrt(p)(sqrt(p)-1), to get 2sqrt(p)(sqrt(p)-1). The diameter is calculated by the distance between two diagonal nodes which is the sum of 2 edges of length sqrt(p)-1.

2-D Torus

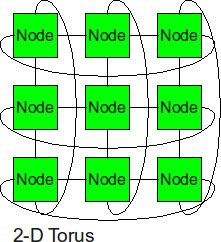
Similarly as the trick we did from linear array to ring topology, the 2-D torus takes the structure of the 2-D mesh and connects the nodes on the edges.

• Diameter sqrt(p)–1
• Bisection BW 2sqrt(p)
• # Links 2p
• Degree 4

With end-around connection, the longest distance has been cut. And the biseciton bandwidth also increased. Of course, the cost from 2-D mesh to 2-D torus almost increased twice.

Cube (3-D Mesh)

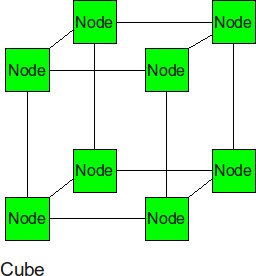
If we add two more neighbor to each node, we can get a cube. The cube can be thought of as a three-dimensional mesh.

• Diameter: 3(p^1/3-1) --this is the corner-to-corner distance, analogous to the 2-d mesh formula
• Bisection BW: p^2/3 -- p^1/3 rows of p^1/3 links must be cut to bisect a cube
• # Links: 3*p^2/3 -- there are p^2/3 links in each of 3 dimensions.
• Degree: 6 (from the inside nodes)

Hypercube

Hypercube

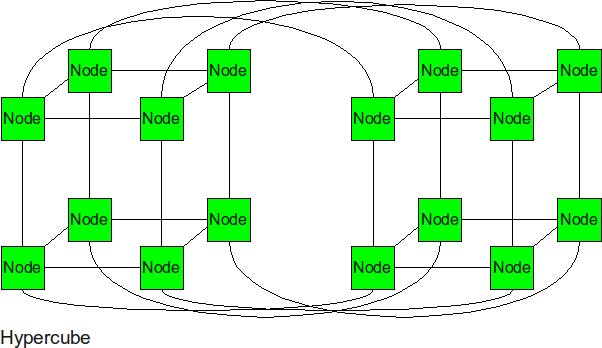
In the N-dimensional cube, the boundary nodes are normally the one who hurts the performance of entire network. Thus, we can fix it by connecting those broundary nodes together. The hypercube is essentially multiple cubes put together.

• Diameter: log₂(p)
• Bisection BW: p/2 -- p/2 links run from one N-1 cube to the other.
• # Links: p/2 * log₂(p) -- each node has a degree of log₂(p). Multiply by p nodes and divide by 2 nodes per link.
• Degree: log₂(p)

From the metrics we can see, the diameter and bisection bandwidth are significantly improved for the high order topologies. Each node is numbered with a bitstring that is log₂(p) bits long. The farthest away node is this bitstring's complement. One bit can be flipped per hop so the diameter is log₂(p).

Tree

Tree

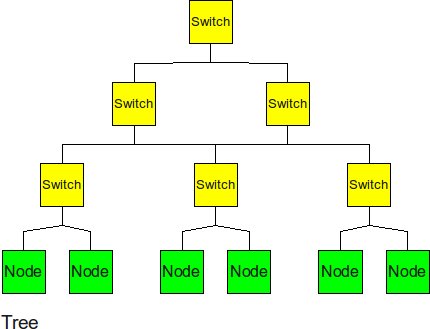
The tree is a hierarchical structure nodes on the bottom and switching nodes at the upper levels.

• Diameter: 2log₂(p) -- the path from a leaf through the root to the farthest leaf on the other side
• Bisection BW: 1 -- breaking either link to the root bisects the tree
• # Links: 2(p-1) -- there are 2 links for each router and there are p routers if p is a power of 2.
• Degree: 3 -- interior routers have a degree of 3.

The tree experiences high traffic at the upper levels. Since almost half of the messages need go through the root node, the root of the tree becomes the bottom neck of the tree topology. Also, the other disadvantage of tree topology is that the bisection bandwidth is only 1.

Fat Tree

Fat Tree

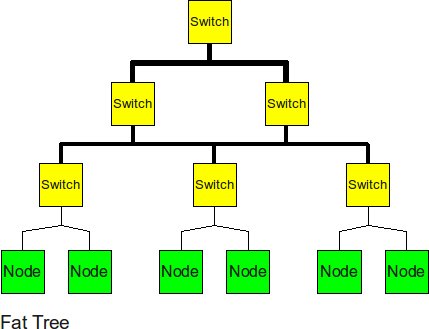
In order to improve the performance of the tree topology, the fat tree alleviates the traffic at upper levels by "fattening" up the links at the upper levels.

• Diameter: 2log₂(p) -- same as a regular tree
• Bisection BW: p/2 -- all links to (one side of) the root must be cut to bisect the tree
• # Links: plog₂(p) -- there are p links at each of log₂(p) levels
• Degree: p -- the root node has p links through it.

The fat tree relieved pressure of root node, the biseciton bandwidth has also been increased.

Butterfly

Butterfly

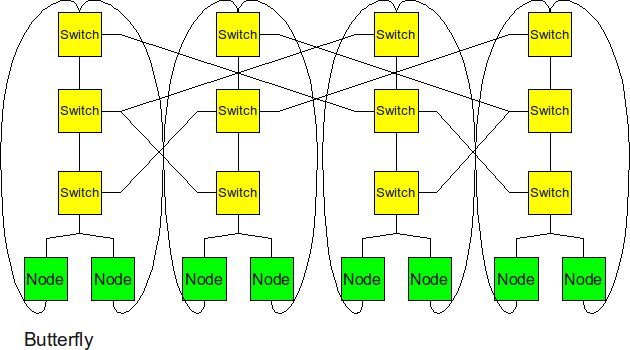
The butterfly structure is similar to the tree structure, but it replicates the switching node structure of the tree topology and connects them together so that there are equal links and routers at all levels.

• Diameter: 2log₂(p) -- same as a tree since butterfly has the same depth as a tree (just with p nodes at each level)
• Bisection BW: p -- p links connect the two halves at the top level
• # Links: 2p*log₂(p) -- there are 2*p links at each level times log₂(p) levels.
• Degree: 4 -- the routers in the middle levels all have 4 links. The leaves and routers at the top level each have 2 links.

Butterfly has similar performance to Hypercube. In terms of cost, butterfly has a smaller degree (so cheaper routers can be used) but hypercube has fewer links.

Real-World Implementation of Network Topologies

In a research study by Andy Hospodor and Ethan Miller, several network topologies were investigated in a high-performance, high-traffic network². Several topologies were investigated including the fat tree, butterfly, mesh, torii, and hypercube structures. Advantages and disadvantages including cost, performance, and reliability were discussed.

In this experiment, a petabyte-scale network with over 100 GB/s total aggregate bandwidth was investigated. The network consisted of 4096 disks with large servers with routers and switches in between².

Basic structure of Hospodor and Miller's experimental network²

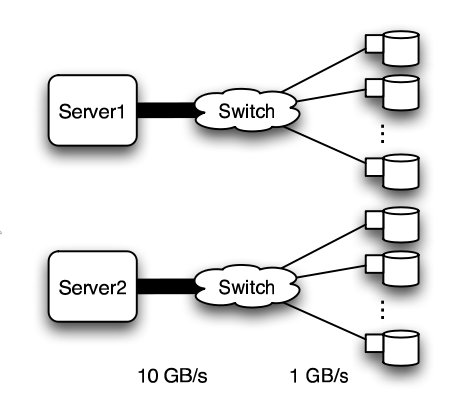
The overall structure of the network is shown below. Note that this structure is very susceptible to failure and congestion.

Fat Tree

In large scale, high performance applications, fat tree can be a choice. However, in order to "fatten" up the links, redundant connections must be used. Instead of using one link between switching nodes, several must be used. The problem with this is that with more input and output links, one would need routers with more input and output ports. Router with excess of 100 ports are difficult to build and expensive, so multiple routers would have to be stacked together. Still, the routers would be expensive and would require several of them².

The Japan Agency for Marine-Earth Science and Technology supercomputing system uses the fat tree topology. The system connects 1280 processors using NEC processors⁷.

Butterfly

In high performance applications, the butterfly structure is a good choice. The butterfly topology uses fewer links than other topologies, however, each link carries traffic from the entire layer. Fault tolerance is poor. There exists only a single path between pairs of nodes. Should the link break, data cannot be re-routed, and communication is broken².

Butterfly structure²

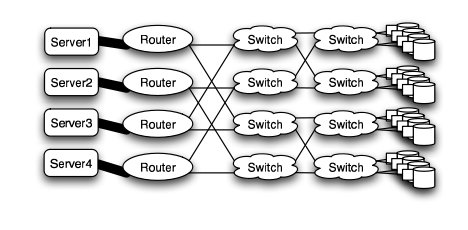
Meshes and Tori

The mesh and torus structure used in this application would require a large number of links and total aggregate of several thousands of ports. However, since there are so many links, the mesh and torus structures provide alternates paths in case of failures².

Mesh structure²

Torus structure²

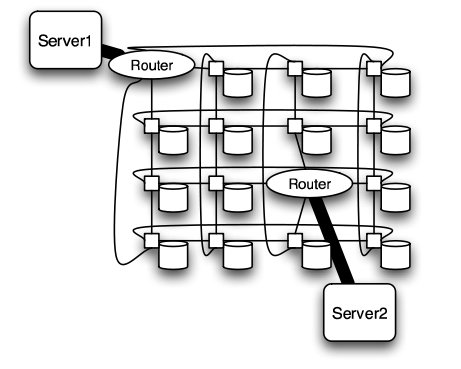
Some examples of current use of torus structure include the QPACE SFB TR Cluster in Germany using the PowerXCell 8i processors. The systems uses 3-D torus topology with 4608 processors⁷.

Hypercube

Similar to the torii structures, the hypercube requires larger number of links. However, the bandwidth scales better than mesh and torii structures.

The CRAY T3E, CRAY XT3, and SGI Origin 2000 use k-ary n-cubed topologies.

Hypercube structure²

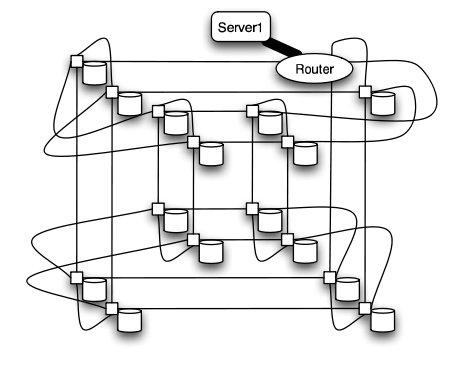
It is worth to mention that even though there are many topologies have much better performance than 2-D mesh, the cost of these advanced topologies are also high. Since most of the chips is in 2-D space, it is very expensive to implement high dimensional topology on 2-D chip. For hypercube topology, the increases of number of node will cause higher degree for each node. For the butterfly topology, although the increases of degree is relatively slow but the required number of links and number of switches increases rapidly.

Comparison of Network Topologies

The following table shows the total number of ports required for each network topology.


Number of ports for each topology²

As the figure above shows, the 6-D hypercube requires the largest number of ports, due to its relatively complex six-dimensional structure. In contrast, the fat tree requires the least number of ports, even though links have been "fattened" up by using redundant links. The butterfly network requires more than twice the number of ports as the fat tree, since it essentially replicates the switching layer of the fat tree. The number of ports for the mesh and torii structures increase as the dimensionality increases. However, with modern router technology, the number of ports is a less important consideration.

Below the average path length, or average number of hops, and the average link load (GB/s) is shown.


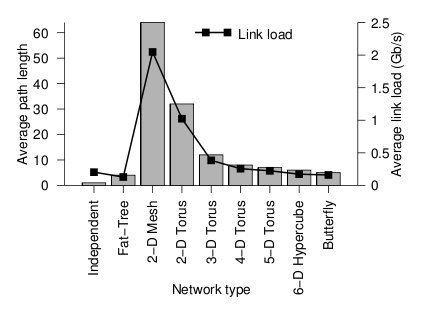
Average path length and link load for each topology²

Looking at the trends, when average path length is high, the average link load is also high. In other words, average path length and average link load are proportionally related. It is obvious from the graph that 2-D mesh has, by far, the worst performance. In a large network such as this, the average path length is just too high, and the average link load suffers. For this type of high-performance network, the 2-D mesh does not scale well. Likewise the 2-D torus cuts the average path length and average link load in half by connected the edge nodes together, however, the performance compared to other types is relatively poor. The butterfly and fat-tree have the least average path length and average link load.

The figure below shows the cost of the network topologies.


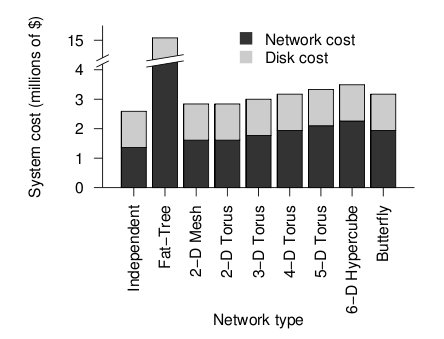
Cost of each topology²

Despite using the fewest number of ports, the fat tree topology has the highest cost, by far. Although it uses the fewest ports, the ports are high bandwidth ports of 10 GB/s. Over 2400, ports of 10 GB/s are required have enough bandwidth at the upper levels of the tree. This pushes the cost up dramatically, and from a cost standpoint is impractical. While the total cost of fat tree is about 15 million dollars, the rest of the network topologies are clustered below 4 million dollars. When the dimensionalality of the mesh and torii structures increase, the cost increases. The butterfly network costs between the 2-D mesh/torii and the 6-D hypercube.

When the cost and average link load is factored the following graph is produced.


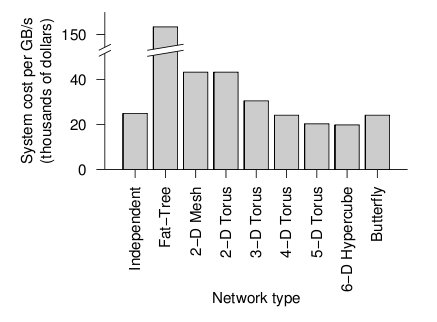
Overall cost of each topology²

From the figure above, the 6-D hypercube demonstrates the most cost effective choice on this particular network setup. Although the 6-D hypercube costs more because it needs more links and ports, it provides higher bandwidth, which can offset the higher cost. The high dimensional torii also perform well, but cannot provide as much bandwidth as the 6-D hypercube. For systems that do not need as much bandwidth, the high-dimensional torii is also a good choice. The butterfly topology is also an alternative, but has lower fault tolerance. However, when the number of nodes increases, the relative cost of the higher-dimensional topologies increases far faster than their relative performance when compared to a 2-D mesh. This is because the 2-D mesh only uses low-cost, short links. The higher-dimensional structures must be projected onto our 3-dimensional world, and thus require many long, expensive links that wrap around the outside of the system like an impenetrable tangle of jungle vines. Maintaining such a network is also quite slow and tedious.

Packet Routing

The routing algorithm determines what path a packet of data will take from source to destination. Routing can be deterministic, where the path is the same given a source and destination, or adaptive, where the path can change. The routing algorithm can also be partially adaptive where packets have multiple choices, but does not allow all packets to use the shortest path³.

Deadlock

When packets are in deadlock when they cannot continue to move through the nodes. The illustration below demonstrates this event.


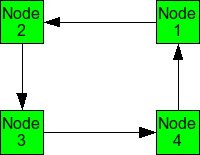
Example of deadlock

Assume that all of the buffers are full at each node. Packet from Node 1 cannot continue to Node 2. The packet from Node 2 cannot continue to Node 3, and so on. Since packet cannot move, it is deadlocked.

The deadlock occurs from cyclic pattern of routing. To avoid deadlock, avoid circular routing pattern.

To avoid circular patterns of routing, some routing patterns are disallowed. These are called turn restrictions, where some turns are not allowed in order to avoid making a circular routing pattern. Some of these turn restrictions are mentioned below.

Dimensional ordered (X-Y) routing

Turns from the y-dimension to the x-dimension are not allowed.

West First

Turns to the west are not allowed.

North Last

Turns after a north direction are not allowed.

Negative First

Turns in the negative direction (-x or -y) are not allowed, except on the first turn.

Odd-Even Turn Model

Unfortunately, the above turn-restriction models reduce the degree of adaptiveness and are partially adaptive. The models cause some packets to take different routes, and not necessarily the minimal paths. This may cause unfairness but reduces the ability of the system to reduce congestion. Overall performance could suffer³.

Ge-Ming Chiu introduces the Odd-Even turn model as an adaptive turn restriction, deadlock-free model that has better performance than the previously mentioned models³. The model is designed primarily for 2-D meshes.

Turns from the east to north direction from any node on an even column are not allowed.
Turns from the north to west direction from any node on an odd column are not allowed.

Turns from the east to south direction from any node on an even column are not allowed.
Turns from the south to west direction from any node on an odd column are not allowed.


The illustration below shows allowed routing for different source and destination nodes. Depending on which column the packet is in, only certain directions are allowed.


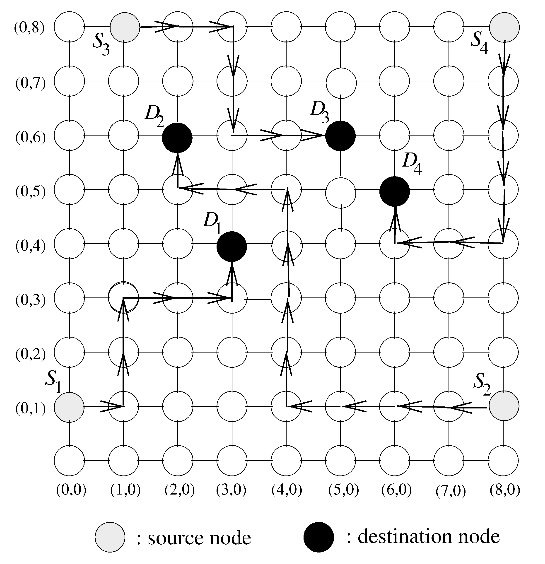
Odd-Even turn restriction model proposed by Ge-Ming Chiu³

Comparison of Turn Restriction Models

To simulate the performance of various turn restriction models, Chiu simulated a 15 x 15 mesh under various traffic patterns. All channels have bandwidth of 20 flits/usec and has a buffer size of one flit. The dimension-ordered x-y routing, west-first, and negative-first models were compared against the odd-even model.

Traffic patterns including uniform, transpose, and hot spot were conducted. Uniform simulates one node send messages to any other node with equal probability. Transpose simulates two opposite nodes sending messages to their respective halves of the mesh. Hot spot simulates a few "hot spot" nodes that receive high traffic.

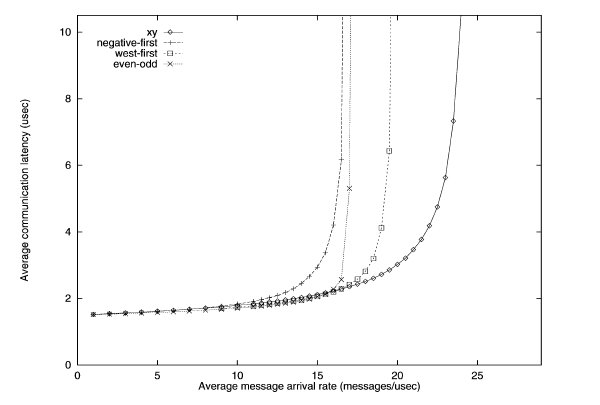
Uniform traffic simulation of various turn restriction models³

The performance of the different routing algorithms is shown above for the uniform traffic. For uniform traffic, the dimensional ordered x-y model outperforms the rest of the models. As the number of messages increase, the x-y model has the "slowest" increase in average communication latency.

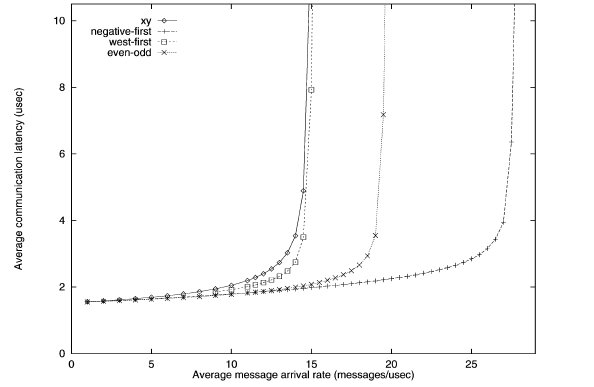
First transpose traffic simulation of various turn restriction models³

The performance of the different routing algorithms is shown above for the first transpose traffic. The negative-first model has the best performance, while the odd-even model performs better than the west-first and x-y models.

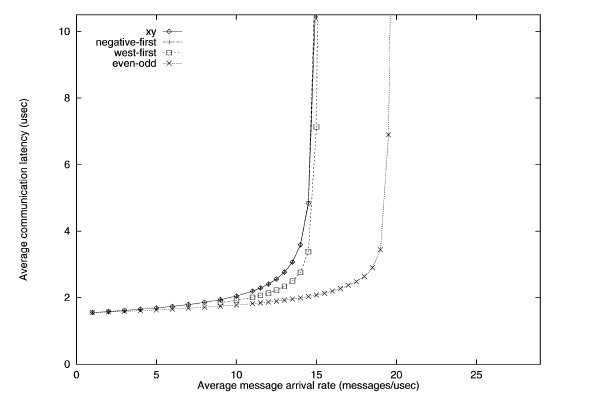
Second transpose traffic simulation of various turn restriction models³

With the second transpose simulation, the odd-even model outperforms the rest.

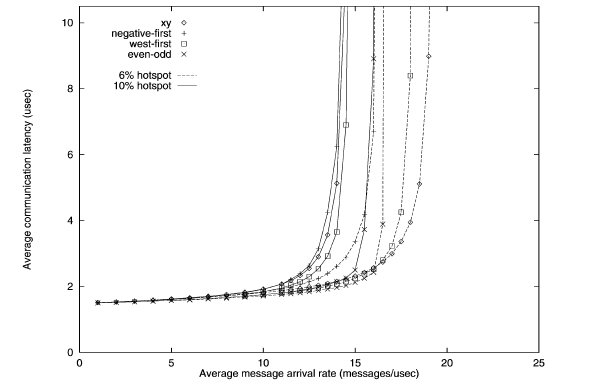
Hotspot traffic simulation of various turn restriction models³

The performance of the different routing algorithms is shown above for the hotspot traffic. Only one hotspot was simulated for this test. The performance of the odd-even model outperforms other models when hotspot traffic is 10%.

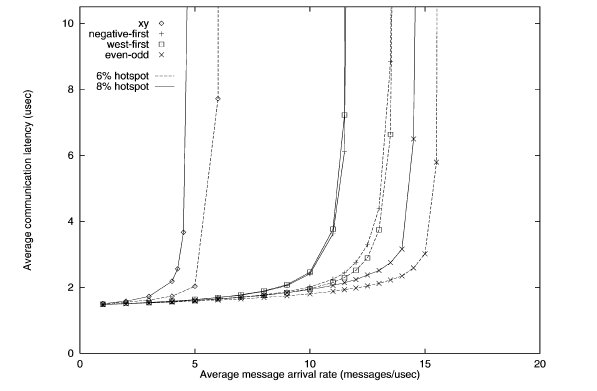
Second hotspot traffic simulation of various turn restriction models³

When the number of hotspots is increased to five, the performance of the odd-even begins to shine. The latency is lowest for both 6 and 8 percent hotspot. Meanwhile, the performance of x-y model is horrendous.

While the x-y model performs well in uniform traffic, it lacks adaptiveness. When traffic becomes hotspot, the x-y model suffers from the inability to adapt and re-route traffic to avoid the congestion caused by hotspots. The odd-even model has superior adaptiveness under high congestion.

Router Architecture

The router is a device that routes incoming data to its destination. It does this by having several input ports and several output ports. Data incoming from one of the inputs ports is routed to one of the output ports. Which output port is chosen depends on the destination of the data, and the routing algorithms.

The internal architecture of a router consists of input and output ports and a crossbar switch. The crossbar switch connects the selects which output should be selected, acting essentially as a multiplexer.

Router technology has improved significantly over the years. This has allowed networks with high dimensionality to become feasible. As shown in the real-world example above, high dimensional torii and hypercube are excellent choice of topology for high-performance networks. The cost of high-performance, high-radix routers has contributed to the viability of these types of high dimensionality networks. As the graph below shows, the bandwidth of routers has improved tremendously over a period of 10 years⁴.

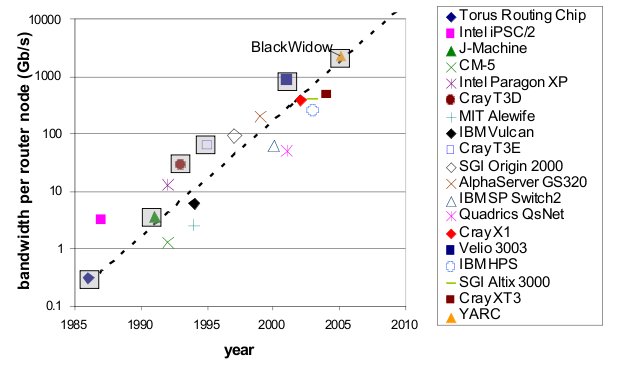
Bandwidth of various routers over 10 year period⁴

Looking at the physical architecture and layout of router, it is evident that the circuitry has been dramatically more dense and complex.

Router hardware over period of time⁴

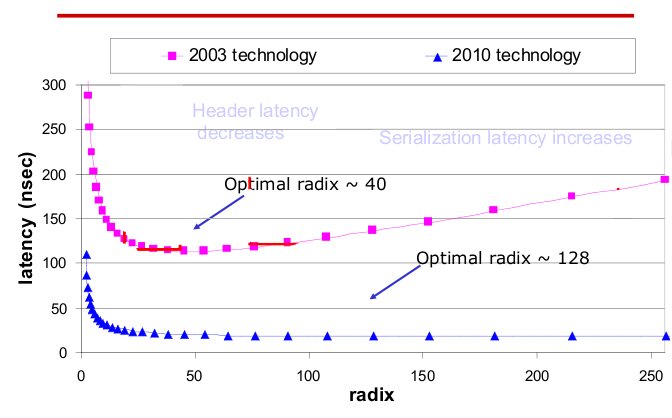
Radix and latency of routers over 10 year period⁴

The radix, or the number of ports of routers has also increased. The current technology not only has high radix, but also low latency compared to last generation. As radix increases, the latency remains steady.

With high-performance routers, complex topologies are possible. As the router technology improves, more complex, high-dimensionality topologies are possible.

Fault Tolerant Routing

Fault-tolerant routing means the successful routing of messages between any pair of non faulty nodes in the presence of faulty components⁶. With increased number of processors in a multiprocessor system and high data rates reliable transmission of data in event of network fault is of great concern and hence fault tolerant routing algorithms are important.

Fault Models

Faults in a network can be categorized in two types:

1.Transient Faults⁵ : A transient fault is a temporary fault that occurs for a very short duration of time. This fault can be caused due to change in output of flip-flop leading to generation of invalid header. These faults can be minimized using error controlled coding. These errors are generally evaluated in terms of Bit Error Rate.

2.Permanent Faults⁵: A permanent fault is a fault that does not go away and causes a permanent damage to the network. This fault could be due to damaged wires and associated circuitry. These faults are generally evaluated in terms of Mean Time between Failures.

Fault Tolerance Mechanisms (for permanent faults)

The permanent faults can be handled using one of the two mechanisms:

1.Static Mechanism: In static fault tolerance model, once the fault is detected all the processes running in the system are stopped and the routing tables are emptied. Based on the information of faults the routing tables are re-calculated to provide a fault free path.

2.Dynamic Mechanisms: In dynamic fault tolerance model, it is made sure that the operation of the processes in the network is not completely stalled and only the affected regions are provided cure. Some of the methods to do this are:

a.Block Faults: In this method many of the healthy nodes in vicinity of the faulty nodes are marked as faulty nodes so that no routes are created close to the actual faulty nodes. The shape of the region could be convex or non-convex, and is made sure that none of the new routes introduce cyclic dependency in the cyclic dependency graph (CDG).

DISADVANTAGE: This method causes lot of healthy nodes to be declared as faulty leading to reduction in system capacity.



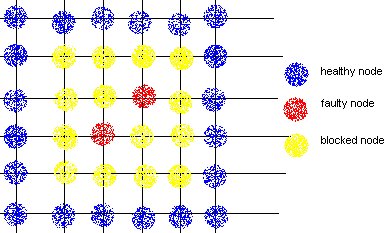
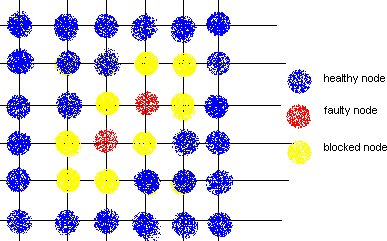
b.Fault Rings: This method was introduced by Chalasani and Boppana. A fault tolerant ring is a set of nodes and links that are adjunct to faulty nodes/links. This approach reduces the number of healthy nodes to be marked as faulty and blocking them.

References

1 Y. Solihin, Fundamentals of Parallel Computer Architecture. Madison: OmniPress, 2009.
2 Interconnection Architectures for Petabyte-Scale High-Performance Storage Systems
3 The Odd-Even Turn Model for Adaptive Routing
4 Interconnection Topologies:(Historical Trends and Comparisons) This link is down at this time. Google Cache
5 Efficient mechanisms to provide fault tolerance in interconnection networks for PC clusters, José Miguel Montañana Aliaga.
6 Adaptive Fault Tolerant Routing Algorithm for Tree-Hypercube Multicomputer, Qatawneh Mohammad
7 TOP500 Supercomputing Sites
8 Understanding and Using the SP Switch
9 Myrinet Overview
10 QsNet (Quadrics' network)
11 Dragonfly Topology
12 Flattened Butterfly Topology