CSC/ECE 506 Spring 2013/4a aj: Difference between revisions
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
===Data/Loop-level Parallelism=== | ===Data/Loop-level Parallelism=== | ||
{| align="right" | {| align="right" | ||
| [[ | | [[Image:grid.png|thumb|right|200px|8x8 Array of processing elements]] | ||
|} | |} | ||
| Line 38: | Line 38: | ||
===Algorithm/Task-level/Functional Parallelism=== | ===Algorithm/Task-level/Functional Parallelism=== | ||
{| align="right" | {| align="right" | ||
| [[Image: | | [[Image:Two_procs.png|thumb|right|200px|Two separate subroutines executing on two separate processors]] | ||
|} | |} | ||
Revision as of 00:56, 14 February 2013
Introduction
Automatic parallelization, also auto parallelization, autoparallelization, or parallelization, the last one of which implies automation when used in context, refers to converting sequential code into multi-threaded or vectorized (or even both) code in order to utilize multiple processors simultaneously in a shared-memory multiprocessor (SMP) machine.<ref>http://en.wikipedia.org/wiki/Automatic_parallelization</ref> Developers desire parallelization as it can provide significant performance gains by reducing the amount of time a particular program or routine takes to complete by spreading the work across multiple processing elements. Ideally, the developer(s) would architect their applications to take advantage of parallel computers, but this may not occur for a few reasons: he/she inherited a sequentially written legacy program, lack of understanding how to program for parallel computers, or the simplicity of developing a sequential program is desired. In these cases, the developer needs to rely on another person to transform the code to support parallel execution or to rely on a compiler to identify and exploit parallelism in the source code. In the past decades the ability of compilers to extract parallelism was minimal or non-existant. Today, a majority of compilers are able to identify and extract parallelism from source code. This wiki article was directed by Wiki Topics for Chapters 3 and 4
Identification
A primary goal of the compiler is to identify opportunities for parallelization and to this end it may use feedback from the developer, high-level language constructs, low-level language constructs, and/or runtime data. Whereas processors focus on instruction-level parallelism and operating systems focus on program-level parallelization, compilers focus on loop-level and task-level parallelization to potentially improve performance. The data parallel style is based on the ability to have part of the data worked on by each processor. The functional style is based on the ability to simultaneously execute different statements or subroutines on different processors.
Data/Loop-level Parallelism
 |
<code>
//Embarrassingly parallel or pleasingly parallel code
for (int i=0; i<N; i++)
{
for (int j=0; j<N; j++)
{
A[i][j] = B[i][j] + C[i][j]; //no dependencies on previous iterations
}
}
</code>
In the code above, both loops can be parallelized. You can imagine an NxN grid of processors, with each processor working on one element of the array. However, this is often not done by compilers as the inner loop often incurs too much overhead, so in this case you can imagine a row of processors with each processor responsible for a single column.
//Not obviously parallelizable code
for (int i=1; i<N; i++)
{
for (int j=1; j<N; j++)
{
A[i][j] = B[i-1][j] + C[i][j-1]; //dependencies on both previous iterations
}
}
However, the code above is parallelizable by sweeping the anti-diagonals. A problem with this approach however will be maintaining a reasonable load across all the processors as some processors will have little work.
Algorithm/Task-level/Functional Parallelism
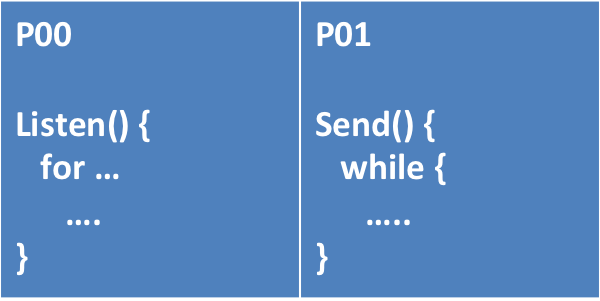 |
<code>
//Functionally parallel code
for (int i=0; i<N; i++)
{
A[i][j] = B[i][j] + C[i][j]; //no dependencies on previous iterations
D[i][j] = E[i][j] + C[i][j]; //no dependencies on previous iterations
}
The above code can be split out as two for loops that execute simultaneously
for (int i=0; i<N; i++)
{
A[i][j] = B[i][j] + C[i][j]; //no dependencies on previous iterations
}
for (int i=0; i<N; i++)
{
D[i][j] = E[i][j] + C[i][j]; //no dependencies on previous iterations
}
</code>
Parallelism was identified by determining that the order of the operations was not important. Therefore, the operations could be conducted in parallel.
High-Level Parallelization Techniques in Compilers<ref>http://www.csc.villanova.edu/~tway/publications/DiPasquale_Masplas05_Paper5.pdf</ref>
Automated parallelization can take place at compile time where the compiler will perform different kinds of analysis in order to determine what can be parallelized. There are many ways to perform this analysis, including scalar analysis, array analysis, and commutativity analysis. By using different types of analysis, the compiler can find different ways that it is possible to parallelize a program. With the growing need for parallel and distributed computing environments, it is often up to the compiler to determine ways in which a users' program can be parallelized. Giving the traditional software developer who hasn't been trained in parallelization technniques a way to automatically parallelize their programs by using a compiler to parallelize their program is advantageous. However, this has proved to be a very difficult task, given that the compiler knows nothing about the program besides the code that it is given. By using different types of analysis like scalar, array, and commutativity analyses, compilers can make an attempt at making a parallelizable program.
Scalar and Array Analysis
Scalar and array analyses are usually performed in conjunction with each other in imperative, low-level languages like C or FORTRAN. "Scalar analysis breaks down a program to analyze scalar variable use and the dependencies that they have." The scalar analysis will find anything that it deems can be parallelized and any sections that it cannot find to be parallelizable, it is left to the array analysis.
One type of array analysis is called array data-flow analysis where the compiler will look for array data that can be privatizable. This privatization can allocate a local copy of an array so different threads in the program can work on different parts of the array. However, if there are any loop-carried dependencies, the analysis will deem that the array is not privatizable, thus not parallizable.
Although these types of analysis are powerful, there are limitations. The most significant limitation is that it cannot support some subsets of the C programming language, which includes pointers. These types of compiler analyses cannot handle pointers since at compile-time it is impossible to determine if a dynamic pointer will contain data objects that are parallelizable. So, this kind of analysis is limited to loop parallelization where a data access pattern is known.
Commutativity Analysis
Unlike scalar and array analysis, commutativity analysis can be used with language more more advanced feature sets, including pointers. "This is a technique that is, 'designed to automatically recognize and exploit commuting operations'". Using the commutativity property in mathematics, the compiler can find ways to automatically parallelize a program. This property is true if two operands, or operations, can be calculated in any order and still produce the same result. In order to test commutativity of an operation, the following conditions are followed:
1. "The new value of each instance variable of the receiver objects of A and B must be the same after the execution of the object section of A followed by the object section of B as after the execution of the object section of B followed by the object section of A"
2. "The multiset of operations directly invoked by either A or B under the execution order A followed by B must be the same as the multiset of operation directly invoked by either A or B under the execution order B followed by A"
In summary, if two operations in a program execute the same method with the same receiver object and the same parameters, then the operation are considered identical by the commutativity property. <ref>http://www.csc.villanova.edu/~tway/publications/DiPasquale_Masplas05_Paper5.pdf</ref>
Polytope Method
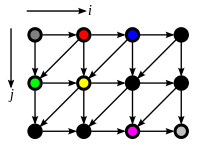
This method represents each iteration of a loop as a vertex point, similar to the familiar Loop-carried Dependency Graphs.
Profile Driven
Deals with input provided by the developer.
Limitations

Luke Scharf, of the National Center for Supercomputing Applications, describes well the limitations of automatic parallelization when he wrote of the problem of parallelization in general, "we usually solve this problem by putting a smart scientist in a room with a smart parallel programmer and providing them a whiteboard and a pot of coffee. Until a compiler can do what these people do, the utility of automatic parallelization is very limited." Compilers are thus limited by the amount and the type of information that is made available to them. Yan Solihin provides a great example of this when describing the ocean current problem in which each loop iteration in the code dependent upon previous iterations. He explains that the code introduces these dependencies, but they are not relevant to solving the problem. At this stage he describes that each point simply takes into account their neighbor and creates a result. Therefore, he discerns that the grid points can be separated by red-black partitioning where each neighbor is a different color, and each partition is assigned to a processor. This is something the compiler will probably never accomplish. Another limitation of compilers is that they must produce results that match results that can be computed serially. When there is a risk that the parallel code will not return the same values as a serial implementation, the compiler must err on the side of caution and fail to parallelize that aspect. [1]
Fine-grained Parallelism
blah blah blah
Course-grained Parallelism
blah blah blah
Examples
Power FORTRAN Analyzer
A powerful commercial product by Silicon Graphics International Corp. When used with Pro MPF it allows for visualization of the parallelization, input from the developer, describes why a loop was not parallelized, and can show the performance of each parallelized loop.<ref>http://www.sgi.com/products/software/irix/tools/prompf.html</ref> An example of output of the analyzer is depicted below in which the compiler determined that the loop was able to be concurrentized/parallelized by scalar analysis.
Footnotes Actions Do Loops Line
DIR 1 # 1 "sample.f"
2 subroutine sample(a,b,c)
3 dimension a(1000),b(1000),c(1000)
SO C +-------- 4 do 10 i = 1,1000
SO *_______ 5 10 a (i) = b(i) + c(i)
6 end
Abbreviations Used
SO scalar optimization
DIR directive
C concurrentized
Loop Summary
From To Loop Loop at
Loop# line line label index nest Status
1 4 5 Do 10 I 1 concurrentized
<ref>http://techpubs.sgi.com/library/dynaweb_docs/0630/SGI_Developer/books/MproPF_PG/sgi_html/ch03.html</ref>
Polaris
Designed in the early 1990s to take a sequential FORTRAN77 program and output an optimized version suitable for execution on a parallel computer. This compiler supported inter-procedural analysis, scalar and array privatization, and reduction recognition.<ref>http://polaris.cs.uiuc.edu/polaris/polaris-old.html</ref>
Stanford University Intermediate Format (SUIF 1,2)
Started out as an NSF-funded and DARPA-funded collaboration between a few universities in the late 1990s with a goal of creating a universal compiler. A major focus of SUIF was parallelization of C source code, and this started with taking an intermediate program representation of the code. At this stage, various automatic parallelization techniques were used including: interprocedure optimization, array privatization, and pointer analysis, reduction recognition.
Jade
A DARPA-funded project that focused on the interactive technique for automatic parallelization. Using this technique, the programmer is able to exploit coarse-grained concurrency.<ref>http://www-suif.stanford.edu/papers/ppopp01.pdf</ref>
Kuck and Associates, Inc. KAP
A commercial compiler that was later acquired by Intel. KAP was an early product which supported FORTRAN and C that featured advanced loop distribution and symbolic analysis.
Intel C and C++ Compilers
A contemporary, advanced compiler that can incorporate multiple parallelization paradigms including: static analysis, interactive, and adaptive/profile-driven. Flags:
-O0, no optimization -O1, optimize without size increase -O2, default optimization -O3, high-level loop optimization -ipo, multi-file inter-procedural optimization -prof-gen, profile guided optimization -prof-use, profile guided optimization -openmp, OpenMP 3.0 support -paralell, automatic parallelization
External links
3.Top500-The supercomputer website
5.Supercomputers to "see" black holes
6.Supercomputer simulates stellar evolution
7.Encyclopedia on supercomputer
10.Water-cooling System Enables Supercomputers to Heat Buildings
13.UC-Irvine Supercomputer Project Aims to Predict Earth's Environmental Future
14.Wikipedia
15.Parallel programming in C with MPI and OpenMP ByMichael Jay Quinn
19.SuperComputers for One-Fifth the Price
References
<references/>