User:Mdcotter

New Interconnection Topologies

Introduction

Parallel processing has assumed a crucial role in the field of supercomputing. It has overcome the various technological barriers and achieved high levels of performance. The most efficient way to achieve parallelism is to employ multicomputer system. The success of the multicomputer system completely relies on the underlying interconnection network which provides a communication medium among the various processors. It also determines the overall performance of the system in terms of speed of execution and efficiency. The suitability of a network is judged in terms of cost, bandwidth, reliability, routing ,broadcasting, throughput and ease of implementation. Among the recent developments of various multicomputing networks, the Hypercube (HC) has enjoyed the highest popularity due to many of its attractive properties. These properties include regularity, symmetry, small diameter, strong connectivity, recursive construction, partitionability and relatively small link complexity.

Metrics Interconnection Networks

Network Connectivity

Network nodes and communication links sometimes fail and must be removed from service for repair. When components do fail the network should continue to function with reduced capacity. Network connectivity measures the resiliency of a network and its ability to continue operation despite disabled components i.e. connectivity is the minimum number of nodes or links that must fail to partition the network into two or more disjoint networks The larger the connectivity for a network the better the network is able to cope with failures.

Network Diameter

The diameter of a network is the maximum internode distance i.e. it is the maximum number of links that must be traversed to send a message to any node along a shortest path. The lower the diameter of a network the shorter the time to send a message from one node to the node farthest away from it.

Narrowness

This is a measure of congestion in a network and is calculated as follows: Partition the network into two groups of processors A and B where the number of processors in each group is Na and Nb and assume Nb < = Na. Now count the number of interconnections between A and B call this I. Find the maximum value of Nb / I for all partitionings of the network. This is the narrowness of the network. The idea is that if the narrowness is high ( Nb > I) then if the group B processors want to send messages to group A congestion in the network will be high ( since there are fewer links than processors )

Network Expansion Increments

A network should be expandable i.e. it should be possible to create larger and more powerful multicomputer systems by simply adding more nodes to the network. For reasons of cost it is better to have the option of small increments since this allows you to upgrade your network to the size you require ( i.e. flexibility ) within a particular budget. E.g. an 8 node linear array can be expanded in increments of 1 node but a 3 dimensional hypercube can be expanded only by adding another 3D hypercube. (i.e. 8 nodes)

Hypercube

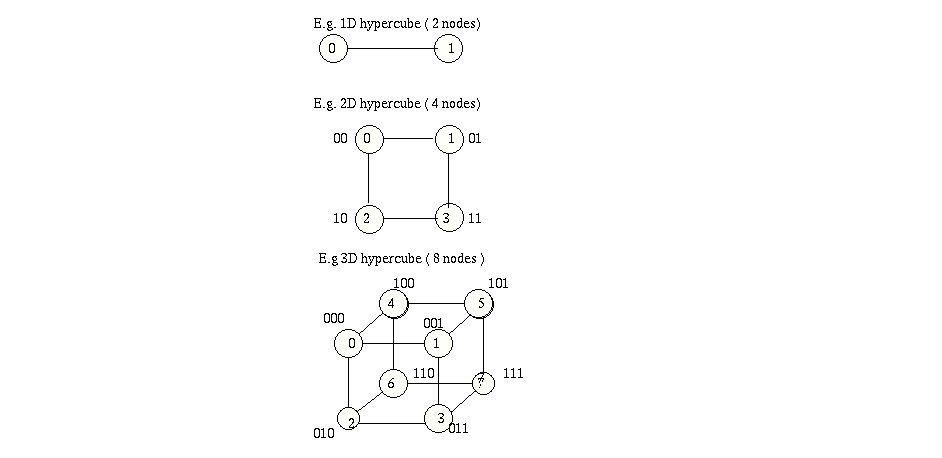
Hypercube networks consist of N = 2n nodes arranged in a k dimensional hypercube. The nodes are numbered 0 , 1, ....2n -1 and two nodes are connected if their binary labels differ by exactly one bit. The attractiveness of the hypercube topology is its small diameter, which is the maximum number of links (or hops) a message has to travel to reach its final destination between any two nodes. For a hypercube network the diameter is identical to the degree of a node n = log2N. There are 2n nodes contained in the hypercube; each is uniquely represented by a binary sequence bn-1bn-2...b0 of length n. Two nodes in the hypercube are adjacent if and only if they differ at exactly one bit position. This property greatly facilitates the routing of messages through the network.

In addition, the regular and symmetric nature of the network provides fault tolerance. Most Important parameters of an interconnection network of a multicomputer system are its scalability and modularity. Scalable networks have the property that the size of the system (e.g., the number of nodes) can be increased with minor or no change in the existing configuration. Also, the increase in system size is expected to result in an increase in performance to the extent of the increase in size. a major drawback of the hypercube network is its lack of scalability, which limits its use in building large size systems out of small size systems with little changes in the configuration. As the dimension of the hypercube is increased by one, one more link needs to be added to every node in the network. Therefore, it becomes more difficult to design and fabricate the nodes of the hypercube because of the large fan-out.

Referecences

<references />