CSC/ECE 506 Spring 2012/10b sr

Use of consistency models in current multiprocessors

The memory consistency model of a shared memory system determines the order in which memory operations will appear to execute to the programmer. This article describes how consistency is used in multiprocessors today and later digs into the details of popular consistency models in use today. The impact of these models on the multiprocessor performance is also discussed.

Introduction

Many modern computer systems and most multicore chips support shared memory in hardware. In a shared memory system, each of the processor cores may read and write to a single shared address space. These designs seek various goodness properties, such as high performance, low power, and low cost. Of course, it is not valuable to provide these goodness properties without first providing correctness. Correct shared memory seems intuitive at a hand-wave level, but, there are subtle issues in even defining what it means for a shared memory system to be correct, as well as many subtle corner cases in designing a correct shared memory implementation. Moreover, these subtleties must be mastered in hardware implementations where bug fixes are expensive.

It is the job of consistency to define shared memory correctness. Consistency definitions provide rules about loads and stores (or memory reads and writes) and how they act upon memory. Ideally, consistency definitions would be simple and easy to understand. However, defining what it means for shared memory to behave correctly is more subtle than defining the correct behavior of, for example, a single-threaded processor core. The correctness criterion for a single processor core partitions behavior between one correct result and many incorrect alternatives. This is because the processor’s architecture mandates that the execution of a thread transforms a given input state into a single well-defined output state, even on an out-of-order core. Shared memory consistency models, however, concern the loads and stores of multiple threads and usually allow many correct executions while disallowing many incorrect ones. The possibility of multiple correct executions is due to the ISA allowing multiple threads to execute concurrently, often with many possible legal interleavings of instructions from different threads. The multitude of correct executions complicates the erstwhile simple challenge of determining whether an execution is correct. Nevertheless, consistency must be mastered to implement shared memory and, in some cases, to write correct programs that use it.

Consistency in current-day multiprocessors

Today's scalable multiprocessors are mostly built with a distributed shared memory architecture. The memory physically distributed but logically shared. In other words, the address spaces generated by all processing nodes globally form a single address space. The main advantage of such a system lies in the scalability with distributed hardware and programmability of a shared virtual memory. Representative systems include the Cray T3D, the Stanford Dash, the MIT Alewife , the Teracomputer, and Convex SPP.

A scalable systems should be able to hide the long latencies of remote memory accesses. Several latency hiding techniques have been proposed: Coherent caches reduce frequency of remote memory accesses by caching data close to the processor. Relaxed memory consistency allows reordering of memory events and buffering or pipelining of remote memory accesses. Data prefetching attempts to hide long read latency by issuing read requests well ahead of time, with the exception that the data will be available in the cache when it is referenced. Multithreading attempts to hide the long latency by context switching between several active threads, thus allowing the processor to perform useful work while waiting for remote requests or synchronization faults to complete.

Consistency models used

Address translation aware memory consistency

These memory consistency models define the behavior of operations (loads, stores, memory barriers, etc.) on physical addresses and virtual addresses. The two important levels of memory consistency that can be classified as address translation aware are described below:

Physical address memory consistency (PAMC)

It is necessary to have correct PAMC for unmapped code to work correctly. Unmapped software, including the boot code and part of the system software that manages AT, relies upon PAMC. It is the responsibility of the hardware to implement PAMC and this is specified precisely in the architectural manual. It is not too difficult to adapt an AT-oblivious consistency model as the specification of PAMC.

Example:

   The PAMC model could be SC. In such a case the interface would specify that 
   (i) there must exist a total order of all loads and stores to physical addresses that respects the program order of each thread and 
   (ii) the value of each load is equal to the value of the most recent store to that physical address in the total order.

Virtual address memory consistency (VAMC)

Correct VAMC is required for mapped code to work correctly.

Although adapting an AT-oblivious consistency model for PAMC is straightforward, there are a few challenges when adapting an AT-oblivious consistency model for VAMC:

• synonyms - Multiple virtual addresses may map to the same physical address. Suppose two virtual addresses VA1 and VA2 map to the same physical address PA. SC requires that the value of a load is equal to the value of the most recent store to the same address. It is possible to have a naive definition of VAMC that does not consider the level of indirection introduced by AT. To overcome this challenge, we re-formulate AT-oblivious consistency models for VAMC by applying the model to synonym sets of virtual addresses rather than individual addresses. For instance, we can define SC for VAMC as follows: there must exist a total order of all loads and stores to virtual addresses that respects program order and in which each load gets the value of the most recent store to any virtual address in the same virtual address synonym set. Incorporating synonyms explicitly in the consistency model allows programmers to reason about the ordering of accesses to virtual addresses.
• mapping and permission changes - Another challenge is that the set of memory operations at the VAMC level is richer than at the PAMC level.
• load/store side effects - Yet another challenge in specifying VAMC is that loads and stores to virtual addresses have certain side effects. The AT system includes status bits such as accessed and dirty bits for each page table entry. These status bits are part of the architectural state, and the ordering of updates to those bits must thus be specified in VAMC. To achieve this we add two new operations to the specification tables: Ld-sb (load’s impact on status bits) and St-sb (store’s impact on status bits).

Causal consistency

Causal Consistency example

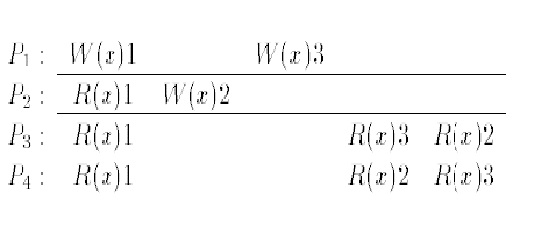
Hutto and Ahamad <ref>P.W. Hutto andM. Ahamad. Slowmemory: Weakening consistency to enhance concurrency in distributed shared memories. In Proceedings of the 10th International Conference on Distributed Computing Systems, pages 302–311,May 1990.</ref> introduced causal consistency. Lamport <ref>Leslie Lamport. Time, clocks, and the ordering of events in a distributed system. Communications of the ACM, 21(7):558–565, 1978.</ref> defined the notion of potential causality to capture the flow of information in a distributed system. This notion can be applied to a memory system by interpreting a write as a message-send event and a read as a message-read event. A memory is causally consistent if all processors agree on the order of causally related events. Causally unrelated events (concurrent events) can be observed in different orders. The example shown here is a legal execution history under CC but not under SC. Note that W(x)1 and W(x)2 are causally related as P2 observed the first write by P1. Furthermore, P3 and P4 observe the accesses W(x)2 and W(x)3 in different orders, which would not be legal in SC.

Delta consistency

The delta consistency model states that after a fixed time period δ, an update is propagated through the system and all replicas will be consistent. In other words, barring a short bounded interval after a modification, the result of any read operation is consistent with a read on the original copy of an object. If an object is modified, the read will not be consistent during the short period of time following its modification. Once the fixed time period elapses, the modification is propagated and the read is now consistent.

Entry consistency

This consistency model has been designed to be used with critical sections. Here, the programmer needs to use acquire and release at the start and end of each critical section just like in both variants of release consistency. However it also required every ordinary shared variable to be associated with a synchronization variable such as a lock or a barrier. If the elements of an array need to be accessed independently in parallel, then each element of the array must be associated with a lock. When an acquire is done on a synchronization variable, only those ordinary shared variables guarded by that synchronization variable are made consistent. Release consistency does not associate shared variables with locks or barriers and at acquire time has to determine empirically which variables it needs. This is where entry consistency differs from release consistency.

Formally, a memory exhibits entry consistency if the following conditions are met:

• An acquire access of a synchronization variable is not allowed to perform with respect to a process until all updates to the guarded shared data have been performed with respect to that process.
• Before an exclusive mode access to a synchronization variable by a process is allowed to perform with respect to that process, no other process may hold the synchronization variable, not even in nonexclusive mode.
• After an exclusive mode access to a synchronization variable has been performed, any other process next nonexclusive mode access to that synchronization variable may not be performed until it has performed with respect to that variable's owner.

Eventual consistency

Given a sufficiently long period of time over which no changes are sent, all updates can be expected to propagate eventually through the system. Thus, all the replicas will be consistent. As the consistency achieved is eventual, the possibility of conflicts is high. The conflicts have to be resolved. There are three types of resolution:

• Read repair: The correction is done when a read finds an inconsistency. This slows down the read operation.
• Write repair: The correction is done when a write operation finds an inconsistency, slowing down the write operation.
• Asynchronous repair: The correction is not part of a read or write operation.

Linearizability

This is also known as strict or atomic consistency. An operation is linearizable if it appears to the rest of the system to occur instantaneously. An atomic operation either occurs completely or does not occur at all. In reality, atomic operations do not actually occur instantaneously. Atomicity is enforced by mutual exclusion. At the software level, locks or semaphores are used to achieve this, while at the hardware level, a cache coherency protocol maybe used. This makes it appear to the user that the entire operation occurred in a single instruction.

A sequence of invocations and responses made of an object by a set of threads is referred to as history. When a function is invoked, a subsequent response is generated.

Example:

   Suppose two threads, A and B attempt to acquire a lock, backing off if it's already taken. 
   This would be modeled as both threads invoking the lock operation, then both threads receiving a response, one successful, one not.  
   A calls lock
   B calls lock
   lock returns fail to A
   lock returns success to B

When all calls make immediate responses, the history is called sequential history. A history that is linearizable is:

• its invocations and responses can be reordered to yield a sequential history
• that sequential history is correct according to the sequential definition of the object
• if a response preceded an invocation in the original history, it must still precede it in the sequential reordering

Now we can reorder the above example in two ways as follows:

Example:

   One way would be:
   A calls lock
   lock returns fail to A
   B calls lock
   lock returns success to B

   The other way would be:
   B calls lock
   lock returns success to B
   A calls lock
   lock returns fail to A

Thus, an object is linearizable if all valid histories of its use can be linearized.

PRAM consistency

PRAM Consistency example

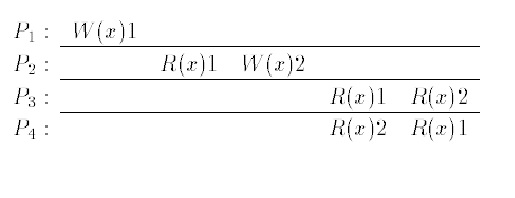
It is also known as FIFO consistency. The reasoning that led to this model was as follows: Consider a multi-processor where each processor has a local copy of the shared memory. For the memory to be scalable, an access should be independent of the time it takes to access the other processors’ memories. They proposed that on a read, a PRAM would simply return the value stored in the local copy of the memory. On a write, it would update the local copy first and broadcast the new value to the other processors. Assuming a constant time for initiating a broadcast operation, the goal of making the cost for a read or write constant is thus achieved. In terms of ordering constraints, this is equivalent to requiring that all processors observe the writes from a single processor in the same order while they may disagree on the order of writes by different processors. The example shown is legal under PRAM but not under SC or CC. P3 and P4 observe the writes by P1 and P2 in different orders, although W(x)1 and W(x)2 are potentially causally related.

Release consistency

Release consistency is one of the consistency models used in the domain of the concurrent programming (e.g. in distributed shared memory, distributed transactions etc.).

Systems of this kind are characterised by the existence of two special synchronisation operations, release and acquire. Before issuing a write to a memory object a node must acquire the object via a special operation, and later release it. Therefore the application that runs within the operation acquire and release constitutes the critical region. The system is said to provide release consistency, if all write operations by a certain node are seen by the other nodes after the former releases the object and before the latter acquire it.

There are two kinds of protocols that implement release consistency:

• eager, where all coherence actions are performed on release operations, and
• lazy, where all coherence actions are delayed until after a subsequent acquire

Sequential consistency

PRAM Consistency example

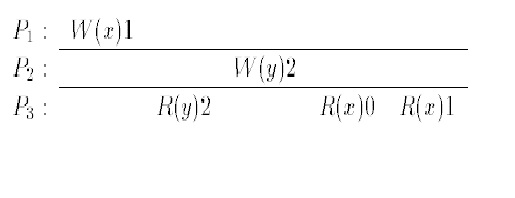
Sequential consistency was first defined by Lamport in 1979. He defined a memory system to be sequentially consistent if: the result of any execution is the same as if the operations of all the processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by it's program.

In a sequentially consistent system, all processors must agree on the order of observed effects. The image to the right shows an example for SC. Note that R(y)2 by processor P3 reads a value that has not been written yet! Of course, this is not possible in any real physical system. However, it shows a surprising flexibility of the SC model. Another reason why this is not a legal history for atomic consistency is that the write operations W(x)1 and W(y)2 appear commuted at processor P3.

Sequential consistency has been the canonical memory consistency model for a long time. However, many multiprocessor machines actually implement a slightly weaker model called processor consistency.

Weak consistency

A memory system is weakly consistent if it enforces the following restrictions:

• accesses to synchronization variables are sequentially consistent and
• no access to a synchronization variable is issued in a processor before all previous data accesses have been performed and
• no access is issued by a processor before a previous access to a synchronization variable has been performed

Notice that the meaning of “previous” is well-defined because it refers to program order. That is, an access A precedes access B if an only if the processor that executed access B has previously executed access A. Synchronizing accesses work as fences. At the time a synchronizing access performs, all previous accesses by that processor are guaranteed not to have performed. The synchronization model corresponding to these access order constraints is relatively simple. A program executing on a weakly consistent system appears sequentially consistent if the following two constraints are observed:

• There are no data races and
• Synchronization is visible to the memory system.

Strong consistency

Strong consistency is one of the consistency models used in the domain of concurrent programming (e.g. in distributed shared memory, distributed transactions etc.). Strong consistency is supported if:

• All accesses are seen by all parallel processes (or nodes, processors etc.) in the same order (sequentially)
• Only one consistent state can be observed. On the other hand, in weak consistency (where different parallel processes or nodes etc.) perceive variables in different states.

Practical performance impact

Implementation of consistency models

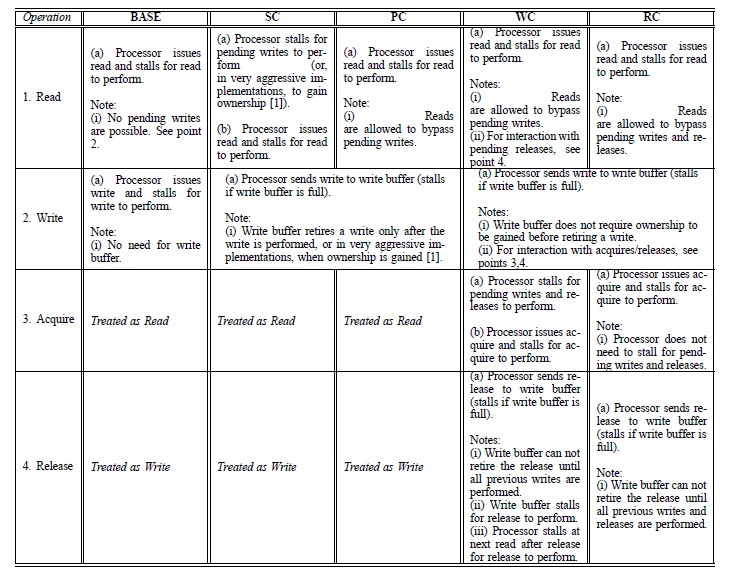
Here, we define performance as the processor utilization achieved in an execution. The reason for using processor utilization as the distinguishing factor is that it provides reasonable results even when the program’s control path is not deterministic and depends on relative timing of synchronization accesses. Let us make a comparative analysis of the performance achieved by the various consistency models on the LFC architecture (an aggressive implementation with lock-free caches).

A BASE model has been added to the four consistency models viz. Sequential Consistency (SC), Processor Consistency (PC), Release Consistency (RC) and Weak Consistency (WC). This is the most constrained model and is used as baseline for all performance comparisons. It incorporates no buffering or pipelining and waits for each read and write to complete before proceeding.

Performance of SC versus BASE

The SC model does not perform significantly better than BASE. The performance gains from BASE to SC is small for most applications. This is because reads are expected to be closely interleaved with writes. Significant write clustering may occur sometimes, for example, when initializing data structures, but such occurrences are expected to be infrequent.

Performance of PC versus SC and BASE

In PC, sequential consistency is abandoned. The main benefit of this extra complexity comes from the fact that reads do not have to stall for pending writes to perform. However, some of the benefits may be lost if the write buffer gets full and stalls the processor. The PC model is relatively successful in hiding almost all of the latency of writes given a reasonably deep write buffer. Since the comparison of PC and WC is more involved than the comparison with RC, we next examine PC versus RC. Subsequently, we compare PC and WC.

Performance of PC versus RC

In addition to providing all the benefits of the PC model, it allows pipelining of writes by exploiting information about the synchronization accesses. That is, writes can be retired from the write buffer before ownership has been obtained. The fact that writes are retired at a faster rate has two implications:

• the write buffer becoming full is less of a problem, and
• in cases where a release operation is behind several writes in the write buffer, that release can be observed sooner by

a processor waiting to do an acquire. The write buffer getting full is really not a problem for PC. Therefore, most gains, if observed, will be due to faster completion of synchronization.

Performance of WC versus PC and RC

The differences between WC and RC arise because WC does not differentiate between acquire and release synchronization operations. Consequently, any synchronization operation must conservatively satisfy the constraints of both release and acquire. Thus, compared to RC, WC stalls the processor at an acquire until pending writes and releases complete. In addition, the processor is stalled for pending releases if it attempts to do a read operation.

On comparing WC and PC we observe a surprising result that PC sometimes performs better than WC. WC has the advantage that writes can be retired at a faster rate from the write buffer. The disadvantage of WC to PC is the same as the disadvantage of WC to RC, in that WC stalls the processor at some points for pending writes and releases to perform.

References

<references/>