CSC/ECE 506 Spring 2012/3a yw: Difference between revisions
(Created page with "Patterns of Parallel Programming -------------------------------------------------------------- ==Introduction== -------------------------------------------------------------- ...") |
No edit summary |
||
| Line 26: | Line 26: | ||
-------------------------------------------------------------- | -------------------------------------------------------------- | ||
In this section, we present a number of commonly used parallel programming patterns. Based on their parallelism forms, we divided the patterns into three categories - functional parallelism, data parallelism and inseparable. The first few patterns are basic patterns represented in graphs. We will focus our discussion on the patterns which uses geometric or mesh data structures. | In this section, we present a number of commonly used parallel programming patterns. Based on their parallelism forms, we divided the patterns into three categories - functional parallelism, data parallelism and inseparable. The first few patterns are basic patterns represented in graphs. We will focus our discussion on the patterns which uses geometric or mesh data structures,recursive data structure and pipeline pattern. | ||
===Functional Parallelism Patterns=== | ===Functional Parallelism Patterns=== | ||
| Line 58: | Line 58: | ||
Suppose the problem involves an operation on a recursive data structure (such as a List, Tree, or Graph) that appears to require sequential processing. How can operations on these data structures be performed in parallel? | Suppose the problem involves an operation on a recursive data structure (such as a List, Tree, or Graph) that appears to require sequential processing. How can operations on these data structures be performed in parallel? | ||
=====Driving Forces===== | =====Driving Forces===== | ||
Recasting the problem to transform an inherently sequential traversal of the recursive data structure into one that allows all elements to be operated upon concurrently does so at the cost of increasing the total work of the computation. This must be balanced against the improved performance available from running in parallel. | |||
This recasting may be difficult to achieve (because it requires looking at the original problem from an unusual perspective) and may lead to a design that is difficult to understand and maintain. | |||
Whether the concurrency exposed by this pattern can be effectively exploited to improve performance depends on how computationally expensive the operation is and on the cost of communication relative to computation on the target parallel computer system. | |||
=====Solutions===== | =====Solutions===== | ||
Latest revision as of 00:38, 12 February 2012
Patterns of Parallel Programming
Introduction
The trend in general purpose microprocessor design has shifted from single-core to chip multiprocessor. The theoretical performance of a multi-core processor is much higher than that of a single-core processor running at similar clock speed. However, despite the rapid advances in hardware performance, the full potential of processing power is not being exploited in the community for one clear reason: difficulty of designing parallel software. <ref>http://www.cs.uiuc.edu/homes/snir/PPP/patterns/concerns.pdf</ref> Parallel programming requires much more effort than serial programming because the programmers need to find the parallelism that exists in an algorithm, and figure out a way to distribute the workload across multiple processors and still get the same result as the serial program. This turned out to be a difficult task. Identifying tasks, designing parallel algorithm, and managing the load balance among many processors has been a daunting task for novice programmers, and even the experienced programmers are often trapped with design decisions that result in suboptimal performance. <ref>http://www.cs.uiuc.edu/homes/snir/PPP/patterns/concerns.pdf</ref> Therefore, to make parallel programming easier for programmers, several common design patterns have been identified over the last decade.
What is a design pattern? It can be defined as quality description of problem and solution to a frequently occuring problem in some domain. <ref>http://www.cs.uiuc.edu/homes/snir/PPP/patterns/patterns.ppt</ref> In the area of parallel programming, design patterns refer to the definition, solution and guidelines for common parallelization problems. Such pattern can take the form of templates in software tools, written paragraphs with detailed description, or charts, diagrams and examples.<ref>http://www.cs.uiuc.edu/homes/snir/PPP/patterns/concerns.pdf</ref> Design patterns implement various types of common process structures and interactions found in parallel systems, but with the key components - the application-specific procedures - unspecified. <ref>http://www.cs.uiuc.edu/homes/snir/PPP/skeleton/dpndp.pdf</ref>
A Sample Pattern
Let's take a look at an example below. Although the example is not related to parallel programming, it gives you a general idea about what exactly a pattern is, which is helpful for understanding the parallel programming patterns we are going to describe in the following sections.

The example describes a lunch pattern. As seen from the figure, a pattern is usually made up of definition, driving forces, solution, benefits, difficulties and related patterns. We will follow this format to describe some of the parallel design patterns.
Why Do We Need Parallel Programming Patterns?
To fully exploit the performance of parallel hardware, programmers need to design their programs in a totally different manner than serial code. This turned out to be a difficult task. The design patterns will guide the programmers systematically to achieve optimal parallel performance by providing them with the framework of parallel programs. The patterns are abstractions of commonly occuring structures and communication characteristics of parallel applications. Programmers just need to fill in their application specific procedures in these patterns, which enables them to develop parallel codes in a faster and easier manner. Also, using the patterns are likely to guarantee the correct operation of parallel application, since the data structures and communication handling codes are well tested. <ref>http://www.cs.uiuc.edu/homes/snir/PPP/skeleton/dpndp.pdf</ref>
Common Parallel Programming Patterns
In this section, we present a number of commonly used parallel programming patterns. Based on their parallelism forms, we divided the patterns into three categories - functional parallelism, data parallelism and inseparable. The first few patterns are basic patterns represented in graphs. We will focus our discussion on the patterns which uses geometric or mesh data structures,recursive data structure and pipeline pattern.
Functional Parallelism Patterns
Functional parallelism focuses on distributing independent tasks across multiple processors. Each processor executes a different thread on the same or different data. Communications occur among the processors while they are executing the codes. We present two patterns in this category.
Embarassingly Parallel Pattern
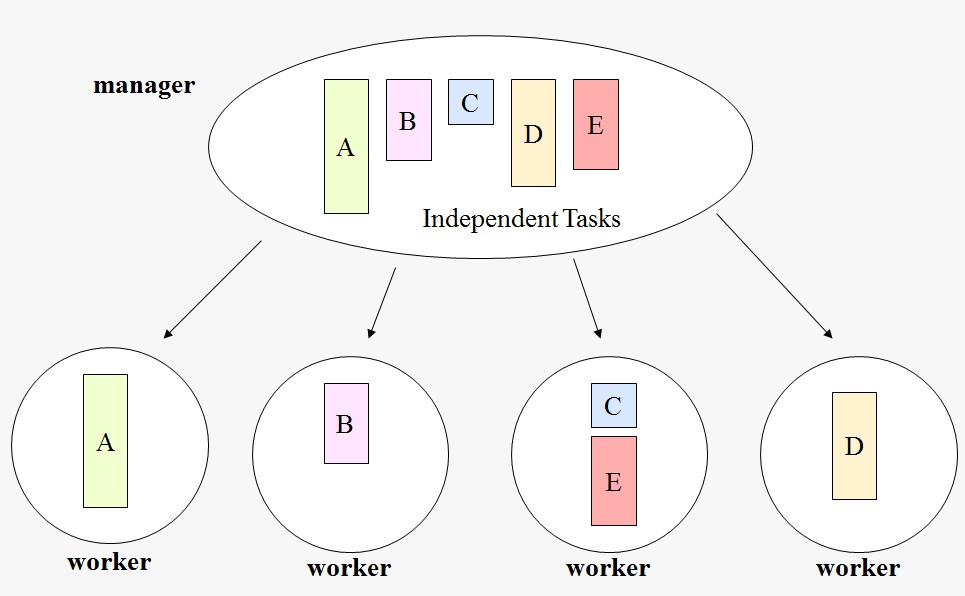
The figure above shows a pattern where we have multiple independent tasks, which are being distributed by the master node to four slave nodes. The tasks are independent of each other so there is no communication between the slave nodes. The communication occurs only between master and slave. The ideal situation is that the master node distribute the same amount of work to each slave node. However, this is dependent of the size of each task, which might vary significantly from one to another. Load balancing is difficult to achieve for this approach.
Divide & Conquer
Divide and Conquer is an approach to solve a big problem by splitting it into several independent smaller problems, which are solved by multiple processors and then the intermediate results are merged to get the final answer. The figure below is a graphical representation of divide and conquer approach. A big problem is divided into multiple smaller problems, which are then distributed to multiple processors. An issue with this approach is that initially when the number of tasks are low, the program is not able to take full advantage of parallel hardware resources. One solution is that we can look for parallelism that exist in each subproblem and try to exploit the parallelism with other patterns.
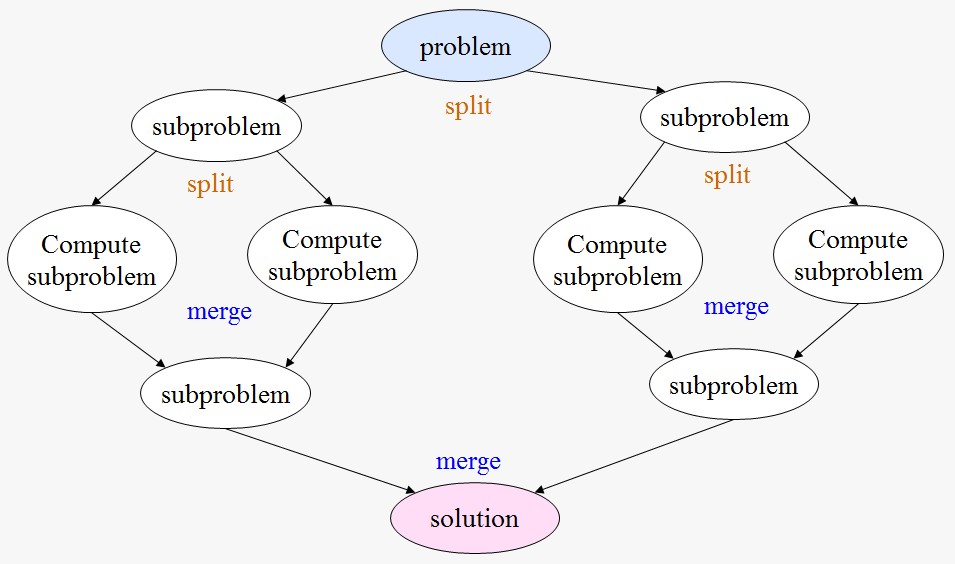
Data Parallelism Patterns
Replicable Pattern
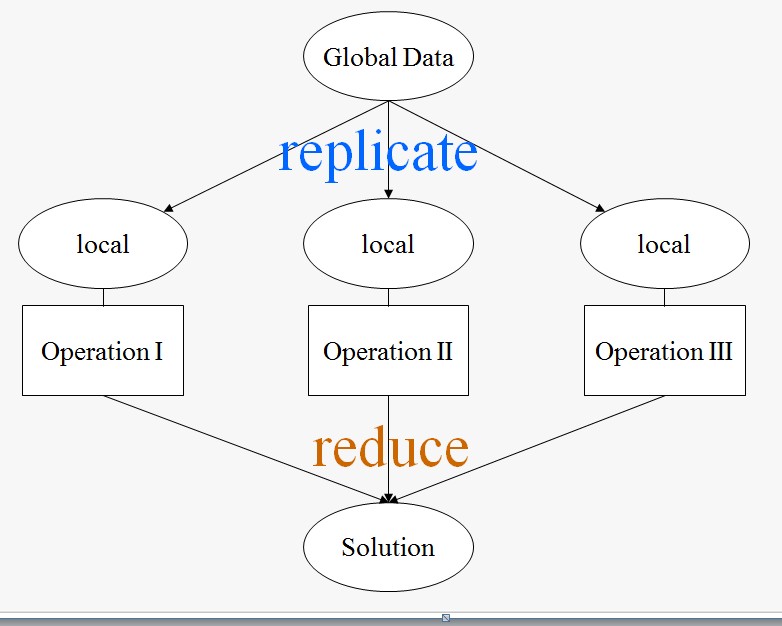
The above figure shows a replicable pattern. The issue is that we need to perform a set of operations on a global data structure, which causes dependency across different threads. To solve this problem, each thread makes a local copy of the required global data, performs a certain operation on that local data and produces a partial result. All the partial results are merged together by the master node to generate the final solution. The merging operation is called reduction. Apparently, this approach can also be considered as a divide and conquer approach.
Repository Pattern
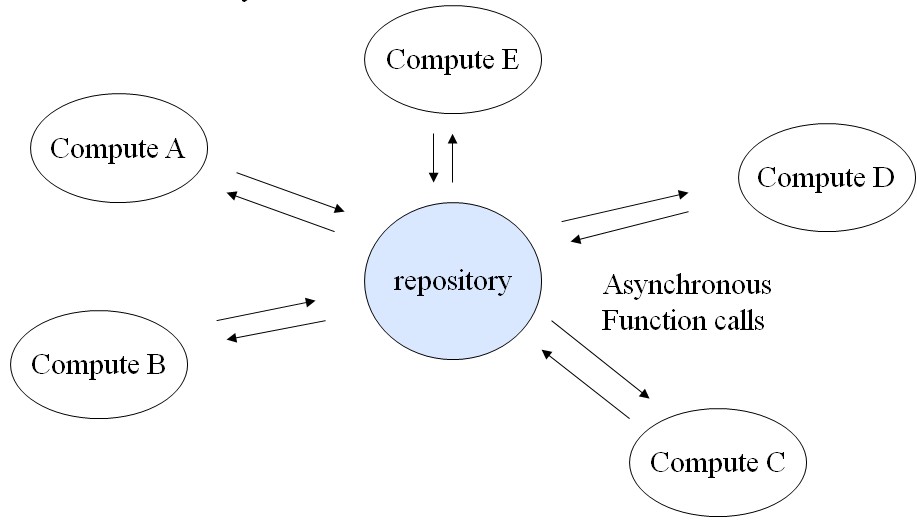
In this case, we have a centralized data structure which is shared by all the computation nodes. Each worker node needs to perform operations on the central data structure in a non-deterministic way. Therefore, the central data structure is controlled by a node to guarantee that each element in the data structure is only accessible by one worker node at any time.
Recursive Data Pattern<ref>Patterns for Parallel Programming, Timothy G. Mattson, ISBN-10: 0321228111</ref>
Problem Description
Suppose the problem involves an operation on a recursive data structure (such as a List, Tree, or Graph) that appears to require sequential processing. How can operations on these data structures be performed in parallel?
Driving Forces
Recasting the problem to transform an inherently sequential traversal of the recursive data structure into one that allows all elements to be operated upon concurrently does so at the cost of increasing the total work of the computation. This must be balanced against the improved performance available from running in parallel. This recasting may be difficult to achieve (because it requires looking at the original problem from an unusual perspective) and may lead to a design that is difficult to understand and maintain. Whether the concurrency exposed by this pattern can be effectively exploited to improve performance depends on how computationally expensive the operation is and on the cost of communication relative to computation on the target parallel computer system.
Solutions
The most challenging part of applying this pattern is restructuring the operations over a recursive data structure into a form that exposes additional concurrency. General guidelines are difficult to construct, but the key ideas should be clear from the examples provided below.
Assuming such situation: Suppose we have a forest of rooted directed trees (defined by specifying, for each node, its immediate ancestor, with a root node's ancestor being itself) and want to compute, for each node in the forest, the root of the tree containing that node. To do this in a sequential program, we would probably trace depth-first through each tree from its root to its leaf nodes; as we visit each node, we have the needed information about the corresponding root. Total running time of such a program for a forest of N nodes would be O(N). There is some potential for concurrency (operating on sub-trees concurrently), but there is no obvious way to operate on all elements concurrently, because it appears that we cannot find the root for a particular node without knowing its parent's root.
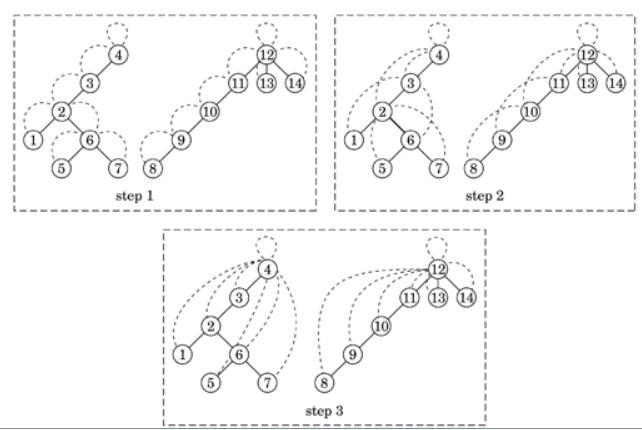
However, a rethinking of the problem exposes additional concurrency: We first define for each node a "successor", which initially will be its parent and ultimately will be the root of the tree to which the node belongs. We then calculate for each node its "successor's successor". For nodes one "hop" from the root, this calculation does not change the value of its successor (because a root's parent is itself). For nodes at least two "hops" away from a root, this calculation makes the node's successor its parent's parent. We repeat this calculation until it converges (that is, the values produced by one step are the same as those produced by the preceding step), at which point every node's successor is the desired value. The figure below shows an example requiring three steps to converge. At each step we can operate on all N nodes in the tree concurrently, and the algorithm converges in at most log N steps.
What we have done is transform the original sequential calculation (find roots for nodes one "hop" from a root, then find roots for nodes two "hops" from a root, etc.) into a calculation that computes a partial result (successor) for each node and then repeatedly combines these partial results, first with neighboring results, then with results from nodes two hops away, then with results from nodes four hops away, and so on. This strategy can be applied to other problems that at first appear unavoidably sequential; the Examples section presents other examples. This technique is sometimes referred to as pointer jumping or recursive doubling.
Example
Algorithms developed with this pattern are a type of data parallel algorithm. They are widely used on SIMD platforms and to a lesser extent in languages such as High Performance Fortran. These platforms support the fine-grained concurrency required for the pattern and handle synchronization automatically because every computation step (logically if not physically) occurs in lockstep on all the processors. Hillis and Steele <ref> W. Daniel Hillis and Guy L. Steele,, Jr. Data parallel algorithms. Communications of the ACM, 29(12): 1170-1183, 1986.</ref> describe several interesting applications of this pattern, including finding the end of a linked list, computing all partial sums of a linked list, region labeling in two-dimensional images, and parsing. Pseudocode for finding partial sums of a list
for all k in parallel
{
temp[k] = next[k];
while temp[k] != null
{
x[temp[k]] = x[k] + x[temp[k]];
temp[k] = temp [temp [k] ];
}
}
In combinatorial optimization, problems involving traversing all nodes in a graph or tree can often be solved with this pattern by first finding an ordering on the nodes to create a list. Euler tour and Ear decomposition are well-known techniques to compute this ordering.
Geometric and Irregular Mesh Pattern<ref> http://www.cs.uiuc.edu/homes/snir/PPP/patterns/AMR.pdf</ref>
Problem Description
Data-parallelism is exposed on a geometric mesh structure (either irregular or regular), Where each point iteratively communicates with nearby neighboring points in computing a Solution until a convergence has been reached. There is a system of formula that Characterizes and governs the global and local behavior of the mesh structure, exposing each partition of mesh elements to different error and accuracy as the computation progresses in steps. Due to the varying error among the partitions, some mesh points provide sufficiently accurate results within a short number of steps, while others exhibit inaccurate results that may require “refined” computation at more fine-grained resolution. Efficiency is an important requirement of the process, thus it is necessary to adaptively refine meshes for selected regions, while leaving out uninteresting part of the domain at a lower resolution.
Driving Forces
- Performance of the adaptively refined computation on the mesh structure must be higher than uniformly refined computation. In other words, the overhead of maintaining adaptive features must be relatively low.
- To provide accurate criterion for further refinement, a good local error estimate must be obtained locally without consulting the global mesh structure. Since global knowledge is limited, useful heuristics must be employed to calculate the local error.
- Efficient data structure needs to be used to support frequent structural resolution change and to preserve data locality across subsequent refinement.
- Partition and re-partition of the mesh structure after each refinement stage must provide each processing unit balanced computational load and minimum communication overhead.
- At each refinement stage, data migration and work stealing needs to be implemented for dynamically balancing the computational load.
Solutions
The solution is an iterative process that consists of multiple components. First, we need an initial partition to divide the mesh points among the processing units. Second, an error indicator that will evaluate how close the locally computed results are to the real solution. Thirdly, when the error is above certain tolerance level, the partition needs to be “refined”, meaning that the mesh size will be reduced by a factor of a constant (usually by power of two). Fourth, as the partition gets altered the mapping of the data elements to the processing units must also be adjusted for better load balance while keeping the data locality at the same time. All these components repeat themselves under efficient data structures designed for efficient access and locality preservation. The outline the algorithm for the Adaptive-Mesh-Refinement pattern, it looks as the following.
n = number of processors;
m = mesh structure;
Initially partition m over n processors;
while (not all partitions satisfy error tolerance) {
compute locally value of partition p;
// using the system of equations.
for each mesh points mp in partition p {
if errorEstimate(mp) > tol) {
mark mp for refinement;
}
}
refine mesh structure where marked;
redistribute m OR
migrate individual data between processors;
}
Example
Barnes-Hut algorithm is used in n-body particle simulation problem, to compute the force between each pair among n particles, and thereby updating their positions. The spatial domain is represented as Quad or Octal tree, and iteratively updated as each particle’s position gets changed during the simulation. One special property that the algorithm exploits is the distance between the particles. If a cluster of particle is located sufficiently far away from another, its effective force can be approximated by using a centre of mass of the cluster (without having to visit individual nodes). This effective force can be calculated recursively, thus reducing the number of traversals required to compute force interactions. Although quite different from partial differential equations, Barnes-Hut also exhibit adaptive refinement aspect in a simply way: it adaptively updates the tree representation depending on the distance of the particles. Unlike PDEs that refines triggered by error condition, Barnes-Hut updates the representation depending on the distance of the particles. The “distance indicator” will act as a guideline in whether to refine or even retract a given data representation as the particle positions move throughout the iterations. As this happens proper load balancing and re-distribution must be followed to increase the performance of the program.
Pipeline Pattern<ref> Patterns for Parallel Programming, Timothy G. Mattson, ISBN-10: 0321228111</ref>
Problem Description
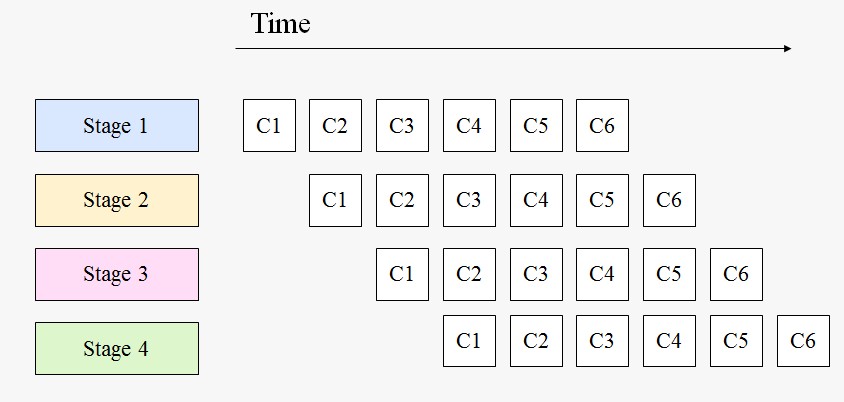
Suppose that the overall computation involves performing a calculation on many sets of data, where the calculation can be viewed in terms of data flowing through a sequence of stages. How can the potential concurrency be exploited? An assembly line is a good analogy for this pattern. Suppose we want to manufacture a number of cars. The manufacturing process can be broken down into a sequence of operations each of which adds some component, say the engine or the windshield, to the car. An assembly line (pipeline) assigns a component to each worker. As each car moves down the assembly line, each worker installs the same component over and over on a succession of cars. After the pipeline is full (and until it starts to empty) the workers can all be busy simultaneously, all performing their operations on the cars that are currently at their stations.
Driving Forces
- A good solution should make it simple to express the ordering constraints. The ordering constraints in this problem are simple and regular and lend themselves to being expressed in terms of data flowing through a pipeline.
- The target platform can include special-purpose hardware that can perform some of the desired operations.
- In some applications, future additions, modifications, or reordering of the stages in the pipeline are expected.
- In some applications, occasional items in the input sequence can contain errors that prevent their processing.
Solutions
The key idea of this pattern is captured by the assembly-line analogy, namely that the potential concurrency can be exploited by assigning each operation (stage of the pipeline) to a different worker and having them work simultaneously, with the data elements passing from one worker to the next as operations are completed. In parallel-programming terms, the idea is to assign each task (stage of the pipeline) to a UE and provide a mechanism whereby each stage of the pipeline can send data elements to the next stage. This strategy is probably the most straightforward way to deal with this type of ordering constraints. It allows the application to take advantage of special purpose hardware by appropriate mapping of pipeline stages to PEs and provides a reasonable mechanism for handling errors, described later. It also is likely to yield a modular design that can later be extended or modified.
Example
A type of calculation widely used in signal processing involves performing the following computations repeatedly on different sets of data.
- Perform a discrete Fourier transform (DFT) on a set of data.
- Manipulate the result of the transform elementwise.
- Perform an inverse DFT on the result of the manipulation.
Inseparable Patterns
There are some other situations that the patterns above cannot fit. However, when some elements are accessed, they need explicit protection. Examples like mutual exclusion and producer-consumer Also, there are some patterns are vaguely defined.
Limitations of Parallel Patterns
Some argue that the parallel patterns identified so far have little to none contribution towards parallel software development. They claim that parallel design patterns are too trivial and fail to give detailed guidelines for specific parameters that can affect the performance of wide range of complex problem requirements. By experience in the community, it is coming to a consensus that there are only limited number of patterns; namely pipeline, master & slave, divide & conquer, geometric, replicable, repository, and not many more. So far the community efforts were focused on discovering more design patterns, but new patterns vary a little and fall into range that is not far from one of the patterns mentioned above. The source of ineffectiveness of these patterns, in fact, does not come from its lack of variety, but it comes from inflexibility of how existing patterns are presented.<ref>http://www.cs.uiuc.edu/homes/snir/PPP/patterns/concerns.pdf</ref>
Comparison
Although the patterns are very different from each other since they should fit different problems, they do have some similarities. They all have to start from decomposing some sequential problem to expose concurrency. As the two categories state above, the Data parallelism patterns expose concurrency from working on different data elements at the same time. On the other hand, Functional parallelism patterns expose concurrency from working on independent functional tasks at the same time<ref> http://www.cs.uiuc.edu/homes/snir/PPP/ </ref>. Also, if focused on some certain patterns which resolve similar problems, we can see that they have something in common. For example, in mesh pattern and pipeline pattern, many dependencies exist. On the other hand, in repository and Dvide & Conquer pattern access same memory location a lot. Many memory protections are needed in such patterns.
Quiz
1. Which of the following is NOT defined by a parallel design pattern?
A. Communication framework
B. Application-specific procedures
C. Data structure
D. Type of parallelism
2. Which of the following is true for embarassingly parallel pattern?
A. Slave nodes communicate to each other
B. Slave nodes only communicate to master node
C. Slave nodes are responsible for load balancing
D. None of the above
3. Which of the following is a characteristic of replicable parallel pattern?
A. Slave nodes perform operations on the global data structure directly.
B. Slave nodes have their own copy of required data.
C. Slave nodes are responsible for reduction.
D. None of the above
4. Which pattern has a centralized data structure which independent computations need to be applied to.
A. Pipeline.
B. Repository.
C. Mesh.
D. Replicable.
5. Which structure(s) can be example(s) of recursive data structure(s)
A. array.
B. list.
C. tree.
D. graph.
6. Barnes-Hut algorithm is an example of which pattern?
A. mesh pattern.
B. pipeline pattern.
C. recursive data pattern.
D. replicable.
7. Which are steps to solve the geometric pattern problem..
A. we need an initial partition to divide the mesh points among the processing units..
B. An error indicator that will evaluate how close the locally computed results are to the real solution.
C. When the error is above certain tolerance level, the partition needs to be “refined”..
D. Setup protection for centralized data structure.
8. Which may be the most challenging part to solve the recursive data structure pattern problem?
A. rewrite to a form can expose concurrency
B. balance the load of each processor
C. protection of data structure
D. deal with dependencies
9. Which pattern can be metaphorized to manufactoria?
A. Pipeline pattern
B. Recursive data pattern
C. Replicable
D. Geometric
10. Which is a practice example for pipeline pattern?
A. signal processing
B. tree traversal
C. ocean simulation
D. Barnes-Hut algorithm
References
<references></references>