CSC/ECE 506 Spring 2011/ch4a zz

Introduction

N-body Problem. Picture source: NASA

The N-body problem stated as follows: Select the position and velocity of n celestial bodies as states. Given the initial condition of of N bodies, compute their states at arbitrary time T. Normally a three-dimensional space is considered for N-body problem. There is a simplified N-body problem called restricted N-body problem where the mass of some of the bodies is negligible. Several remarkable three-body simulation can be found in [1].

The trajectory of restricted three-body system.

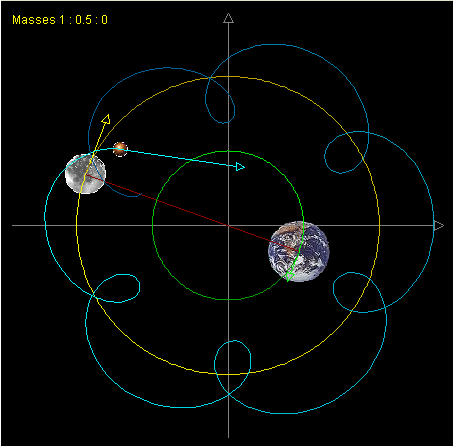
Many mathematicians have proofed that it is impossible to find a general solution for n-body problem analytically[2]. The system could become unstable very easily. However, the problem can be solved numerically. The most common approach is to iterate over a sequence of small time steps. Within each time step, the acceleration on a body is approximated by the transient acceleration in the pervious time step. The transient acceleration on a single body can be directly computed by summing the gravity from each of the other N-1 bodies. While this method is conceptually simple and is the algorithm of choice for many applications, its O(N²)

The simulation of N-body system can be used from simulation of celestial bodies (gravitational interaction)to interactions of a set of particles (electromagnetic interaction).

References

[1] [1] Collection of remarkable three-body motions

[2][[2]] something about Poincaré

[3] Diacu, F (01/01/1996). "The solution of the n-body problem". The Mathematical intelligencer (0343-6993), 18 (3), p. 66.