CSC 216/s08/eschew disenchantment

Formatting Resources

Formatting Help Guide from MetaWiki

The Hierarchical Merge Sort

The problem

In this exercise, we want to teach students the mechanics of a merge sort algorithm.

Participants and props

Seven students will participate in the exercise. They will need seven numbered note cards, scotch tape, and a series of hats. There should be seven hats as follows: One master hat, two delegate hats, and four peon hats.

The script

Setup

1. There should be a pseudocode description of the merge sort algorithm on a large display.
2. The numbered notecards must be taped together in a randomly ordered line.
3. Students should be shown an animation of the merge sort algorithm (shown here).

Pseudo Code

public int[] mergeSort(int[] m) {

    if (m.length == 1) Return m
    if (m.length == 2) Sort m, then return m
    Split m in half
    Call mergeSort on each half
    Merge the two halves after they are sorted and returned (iterative merge of two ordered arrays)
    Return the array

}

An example of a merge sort, showing the arrays through the process.

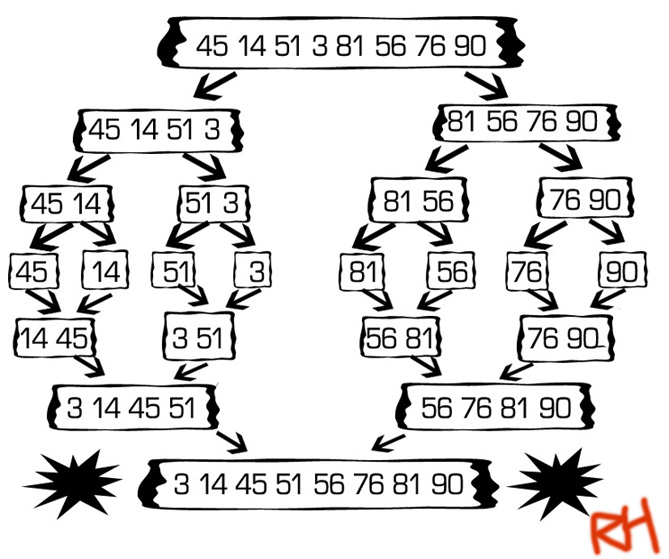
Activity

First, the seven hats need to be assigned to the seven students. Then the student wearing the king hat should perform as though he is the initial call to mergeSort(). The king should use his delegates to handle his recursive mergeSort calls. The delegates should use their peons to handle their own mergeSort() calls.

When it is time for a participant to merge two ordered lists, they may do so without adhering to any algorithm.