CSC/ECE 506 Spring 2015/7a ap: Difference between revisions
No edit summary |
|||
| (6 intermediate revisions by the same user not shown) | |||
| Line 35: | Line 35: | ||
In this example, initially, the values of ''x'', ''y'', ''z'', ''xReady'' and ''xyReady'' are zero. | In this example, initially, the values of ''x'', ''y'', ''z'', ''xReady'' and ''xyReady'' are zero. Consider that the code when executed follows program program order that is S1 -> S2 -> S3 -> S4 -> S5 -> S6 -> S7. | ||
So as per the code, firstly P0 executes its statements S1 and S2 in order and sets their values as 5 and 1 respectively. P1 receives the signal 1 from P0 and comes out of the loop in S3. P1 then reads the value of ''x'' and sets the value of ''y'' and ''xyReady'' as 9 and 1 respectively. P3 then receives the signal ''xyReady'' as 1 so it reads the value of ''x'' and ''y'' and sets the value of ''z''. The programmer expects that the value of z should be 45 (5*9) due to the atomicity of the execution of | So as per the code, firstly P0 executes its statements S1 and S2 in order and sets their values as 5 and 1 respectively. P1 receives the signal 1 from P0 and comes out of the loop in S3. P1 then reads the value of ''x'' and sets the value of ''y'' and ''xyReady'' as 9 and 1 respectively. P3 then receives the signal ''xyReady'' as 1 so it reads the value of ''x'' and ''y'' and sets the value of ''z''. The programmer expects that the value of ''z'' should be 45 (5*9) due to the atomicity of the execution of instructions. | ||
[[Image:MCM_eg_2.png|thumbnail|right|400px|Figure 1: Example 2 for Memory Consistency<sup><span id="3body"></span></sup>]] | [[Image:MCM_eg_2.png|thumbnail|right|400px|Figure 1: Example 2 for Memory Consistency<sup><span id="3body"></span></sup>]] | ||
Now, consider the scenario given in ''Figure 1''. P0 executes S1, which writes a value of 5 to ''x''. This write is then propagated to P1 and P2, however it reaches P1 faster | Now, consider the scenario given in ''Figure 1''. P0 executes S1, which writes a value of 5 to ''x''. This write is then propagated to P1 and P2, however it reaches P1 faster than P2. Then, P0 performs a write to ''xReady'', which is also propagated to P1. P1 now sees the new values of ''xReady'' and ''x''. So P1 executes its S4 statement, assigning a value of 9 to ''y'', and then sets ''xyReady'' to 1 which is propagated to P2. P2 then comes out of its loop and reads the value of ''x'' and ''y''. Since the value of ''x'' from P0 has yet not reached P2, P2 reads a fresh value of ''y'' but the stale value of ''x''. Thus the output of the program is unexpected which in this case is ''z'' = 0. | ||
From the first and second example it is clear that the implicit expectation of | From the first and second example it is clear that the implicit expectation of a programmer is: | ||
* Memory accesses performed by a single processor should be occurred in program order and | * Memory accesses performed by a single processor should be occurred in program order and | ||
| Line 60: | Line 60: | ||
==Types of Memory Consistency Models== | ==Types of Memory Consistency Models== | ||
Following Tree (''Figure 2'') shows different Memory Consistency models according to their | Following Tree (''Figure 2'') shows different Memory Consistency models according to their weakening order. A model is said to be weaker compared to another model if it has less restrictions. | ||
[[Image:MCM_tree_new2.png|thumbnail|center|1000px|Figure 2: Types of Memory Consistency Models<sup><span id="3body"></span></sup>]] | [[Image:MCM_tree_new2.png|thumbnail|center|1000px|Figure 2: Types of Memory Consistency Models<sup><span id="3body"></span></sup>]] | ||
| Line 93: | Line 93: | ||
The second aspect makes it appear as if one memory operation executes atomically or instantaneously with respect to other memory operations. This model is weaker than Strict Consistency model as this model does not require all changes to be propagated instantaneously to all the other processors in the system. | The second aspect makes it appear as if one memory operation executes atomically or instantaneously with respect to other memory operations. This model is weaker than Strict Consistency model as this model does not require all changes to be propagated instantaneously to all the other processors in the system. | ||
''Figure 4'' represents how the different loads and stores are performed when Sequential Consistency Model is used in the hardware. P1 stores a value “a” then P2 stores a value “b”. P3 reads the value | ''Figure 4'' represents how the different loads and stores are performed when Sequential Consistency Model is used in the hardware. P1 stores a value “a” then P2 stores a value “b”. P3 reads the value stored by P1 then P4 reads the value stored by P2 and so on. At each time, a single memory access operation is performed. Both P3 and P4 read the values stored by P1 and P2 in the proper order as they are propagated. | ||
====Basic Implementation of Sequential Consistency==== | ====Basic Implementation of Sequential Consistency==== | ||
| Line 108: | Line 108: | ||
Here, it is clear that Step 1 and Step 4 are not affected by other memory accesses. Effective address (Step 1) is computed in the functional unit which involves computation not access. Similarly the final value to be loaded in the destination register (Step 4) has already been fetched from the cache so it does not involve any further memory access. Thus, it can be concluded that the actual load (which involves memory access) starts from Step 2 and ends on Step 3. These two steps should be performed atomically. | Here, it is clear that Step 1 and Step 4 are not affected by other memory accesses. Effective address (Step 1) is computed in the functional unit which involves computation not access. Similarly the final value to be loaded in the destination register (Step 4) has already been fetched from the cache so it does not involve any further memory access. Thus, it can be concluded that the actual load (which involves memory access) starts from Step 2 and ends on Step 3. These two steps should be performed atomically. | ||
Consider a store | Consider a store operation. A store operation is completed in below four steps: | ||
* '''Step 1:''' Computation of effective address in a functional unit. | * '''Step 1:''' Computation of effective address in a functional unit. | ||
* '''Step 2:''' The store is | * '''Step 2:''' The store is committed by copying the destination address and the latest value to be stored to a write buffer. | ||
* '''Step 3:''' The store value in the write buffer is released to the cache. | * '''Step 3:''' The store value in the write buffer is released to the cache. | ||
* '''Step 4:''' The store is considered complete when this new value is fully propagated to the other processors. | * '''Step 4:''' The store is considered complete when this new value is fully propagated to the other processors. | ||
As the store involves multiple cache values thus effectively the store starts when the destination address is issued and the latest value is stored in the write buffer in Step 2 till | As the store involves multiple cache values thus effectively the store starts when the destination address is issued and the latest value is stored in the write buffer in Step 2 till Step 4 where the store is fully propagated to other caches. So these steps should be performed atomically. It can be concluded that the basic implementation of SC inflicts a lot of restrictions on how the instructions within a program have to be executed and thus it affects the performance. So in order to improve the performance of SC, few optimizations in the model are possible. | ||
====Techniques to improve Sequential Consistency performance==== | ====Techniques to improve Sequential Consistency performance==== | ||
Performance of a Sequential Consistency | Performance of a Sequential Consistency model can be improved if the execution of memory accesses is made faster and when it is allowed for the memory accesses to be overlapped with respect to one another as listed below, | ||
* The first performance enhancement technique avoids the overlapping of execution of loads and stores but involves overlapping of the data fetches that are generated by these loads and stores. In this technique, load/store prefetching is performed on the data which is to be used in the coming load/store by changing the state of the cache block to S (load prefetching) or M (store prefetching). Thus when the actual load/store memory access is performed then it takes less time to complete. | * The first performance enhancement technique avoids the overlapping of execution of loads and stores but involves overlapping of the data fetches that are generated by these loads and stores. In this technique, load/store prefetching is performed on the data which is to be used in the coming load/store by changing the state of the cache block to '''S''' (load prefetching) or '''M''' (store prefetching). Thus when the actual load/store memory access is performed then it takes less time to complete. | ||
* The second technique of performance enhancement depends on speculation access where the execution of a load can be overlapped with the execution of the older load by speculatively assuming that the older load is executed atomically. If the older load does not get executed atomically then this younger load is canceled and it is executed again. This speculative execution is typically only implemented for loads. All stores are issued to the cache atomically only. | * The second technique of performance enhancement depends on speculation access where the execution of a load can be overlapped with the execution of the older load by speculatively assuming that the older load is executed atomically. If the older load does not get executed atomically then this younger load is canceled and it is executed again. This speculative execution is typically only implemented for loads. All stores are issued to the cache atomically only. | ||
===Relaxed Consistency Models=== | ===Relaxed Consistency Models=== | ||
These models basically loosen up the memory access restrictions of Sequential Consistency model. As these models do not put a lot of restriction on the sequence of the memory accesses thus their performance is better than Sequential Consistency | These models basically loosen up the memory access restrictions of Sequential Consistency model. As these models do not put a lot of restriction on the sequence of the memory accesses thus their performance is better than Sequential Consistency model. But the implementations of these models require a lot of complexity in the program. During coding, the programmers have to make sure that their programs obey the rules of the consistency model that the hardware provides. | ||
Relaxation in the memory accesses may allow the order of execution of the instructions in a program different from the programmer’s expectation. Thus to prevent any non-deterministic outcome of the program, safety net is provided to the programmers to implement it in their | Relaxation in the memory accesses may allow the order of execution of the instructions in a program different from the programmer’s expectation. Thus to prevent any non-deterministic outcome of the program, safety net is provided to the programmers to implement it in their programs to specify strict ordering between a pair of memory accesses. This safety net is provided in terms of fence instruction. Once a fence instruction is implemented in the program then it prohibits all the memory accesses following it until all the memory accesses before it have been completed. Fence instruction is of two types. When the fence is only applied to the stores such that there is a proper ordering of the memory accesses between all the stores before the fence and all following it then such type of fence is called '''store fence/barrier'''. On the other side, when the fence is only applied to the loads such that there should be perfect ordering between the loads before the fence appears and the loads after the fence then such a fence is called '''load fence/barrier'''. | ||
[[Image:MCM_CC_eg.png|thumbnail|right|400px|Figure 5: Representation | [[Image:MCM_CC_eg.png|thumbnail|right|400px|Figure 5: Representation of any Load or Store in Causal Consistency<sup><span id="3body"></span></sup>]] | ||
When a fence is implemented in the program then all the memory accesses younger than fence are flushed out from the pipeline. Firstly all the memory accesses older than fence are completed and then the processor state is restored to the state prior to the fence instruction and execution is resumed from that point. | When a fence is implemented in the program then all the memory accesses younger than fence are flushed out from the pipeline. Firstly all the memory accesses older than fence are completed and then the processor state is restored to the state prior to the fence instruction and execution is resumed from that point. | ||
| Line 136: | Line 136: | ||
===Causal Consistency Model=== | ===Causal Consistency Model=== | ||
''[http://en.wikipedia.org/wiki/Causal_consistency Causal Consistency Model]'' <ref>http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.50.3356</ref> is a weaker | ''[http://en.wikipedia.org/wiki/Causal_consistency Causal Consistency Model]'' <ref>http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.50.3356</ref> is a weaker model of Sequential Consistency model. Here, a differentiation is made between events that are potentially causally connected with each other and those that are not. A system provides Causal Consistency if memory operations that potentially are causally related are seen by every processor of the system in the same order. Operations that are not causally related are said to be concurrent. Concurrent writes may be seen in different order by different processors but Condition-writes (i.e. ones that are potentially causally related) must be seen by all processors in the same order. Causal Consistency model is weaker than Sequential Consistency model in the sense that all the concurrent writes in this model can be seen in any order by all the other processors in the system while they are required to be seen in the same order by other processors in Sequential Consistency. | ||
When a store operation follows a load operation performed by a processor then the load and store are considered causally connected. Similarly, when a load operation follows a store operation then it is also considered causally connected. Also, the transitive closure of the previous two types of pairs of operations are also causally related. | When a store operation follows a load operation performed by a processor then the load and store are considered causally connected. Similarly, when a load operation follows a store operation then it is also considered causally connected. Also, the transitive closure of the previous two types of pairs of operations are also causally related. | ||
''Figure 5'' shows | ''Figure 5'' shows an order of loads and stores in this model. Store operation w(x)1 by processor P1 is causally related to store operation w(x)2 by processor P2 but the store operations w(x)3 by processor P1 and w(x)2 by processor P2 are concurrent writes thus can be seen in any order by processor P3 and P4. | ||
===Processor Consistency Model=== | ===Processor Consistency Model=== | ||
| Line 146: | Line 146: | ||
[[Image:MCM_ProcessorC_egnew.png|thumbnail|right|400px|Figure 6: Representation of Order of any Load or Store in Processor Consistency<sup><span id="3body"></span></sup>]] | [[Image:MCM_ProcessorC_egnew.png|thumbnail|right|400px|Figure 6: Representation of Order of any Load or Store in Processor Consistency<sup><span id="3body"></span></sup>]] | ||
Processor Consistency | Processor Consistency model is a weaker model than Causal Consistency. In Sequential Consistency a proper ordering is forced on all the memory accesses, which are, Load -> Load, Load -> Store, Store -> Store, and Store -> Load. The basic implementation of a Processor Consistency Model is based on relaxing the ordering between an older store and a younger store (Store -> Load). In this model, when a store has not completed, a younger load is allowed to issue to the cache and even complete. The importance of this is that store instructions can be queued in the write buffer and be completed at a later time without the use of load speculation. In the mean time, loads do not require to wait for the older stores to complete and can access the cache and hence they reduce the load latency. In case of Processor Consistency, when a load is issued to the cache then it is not rolled back even if the illusion of atomicity is broken in contrast to SC where the load is rolled back at once. This result is better performance of Processor Consistency as compared to Sequential Consistency. Processor Consistency only relaxes one ordering rule out of four, hence it only affects the correctness of code that has a store followed by a load. If a program is a properly synchronized program, PC provides the same outcome as Sequential Consistency. In a post and wait synchronization in which a processor produces a data value and sets a flag to signal the availability of the new value. This involves at least two store instructions, which are ordered with respect to each other in Processor Consistency. Once the consumer sees the flag high, it performs at least two loads and this ordering is also guaranteed under Processor Consistency. Thus, post and wait sync produces the same outcome in Processor Consistency as in Sequential Consistency. | ||
Processor Consistency | Processor Consistency model is weaker than Causal Consistency model in the sense that it requires all the stores performed by a single processor to be seen in the same order by different processors in the system as they are issued but stores performed by the different processors can be seen in any order by other processors in the system while in Causal Consistency all causally related stores are required to be seen in the same order by all the processors. Some definitions of Processor Consistency model involve the concept of cache coherence thus if there are two different stores performed by two different processors on the same memory location then the model requires that these stores are to be seen in the same order by the different processors in the system as they are issued. | ||
''Figure 6'' represents the same concept. Two stores w(x)1 and w(x)2 are performed by two different processors P1 and P2 but as they are performed on the same memory location thus the same order is required to be seen by processor P3 and P4. | ''Figure 6'' represents the same concept. Two stores w(x)1 and w(x)2 are performed by two different processors P1 and P2 but as they are performed on the same memory location thus the same order is required to be seen by processor P3 and P4. | ||
===PRAM Consistency Model=== | ===PRAM Consistency Model=== | ||
[[Image:MCM_PRAMC_eg.png|thumbnail|right|400px|Figure 7: Representation of Order of any Load or | [[Image:MCM_PRAMC_eg.png|thumbnail|right|400px|Figure 7: Representation of Order of any Load or Store in PRAM Consistency <sup><span id="3body"></span></sup>]] | ||
''[http://en.wikipedia.org/wiki/PRAM_consistency PRAM Consistency Model]'' <ref>http://cs.gmu.edu/cne/modules/dsm/orange/pram_con.html</ref> <ref>http://www.e-reading.link/chapter.php/143358/220/Tanenbaum_-_Distributed_operating_systems.html</ref>is pipelined random access memory consistency. It is also known as FIFO consistency. This consistency model is even more relaxed than Processor Consistency | ''[http://en.wikipedia.org/wiki/PRAM_consistency PRAM Consistency Model]'' <ref>http://cs.gmu.edu/cne/modules/dsm/orange/pram_con.html</ref> <ref>http://www.e-reading.link/chapter.php/143358/220/Tanenbaum_-_Distributed_operating_systems.html</ref>is pipelined random access memory consistency. It is also known as FIFO consistency. This consistency model is even more relaxed than Processor Consistency model. In this model, all processors see the stores performed by one processor in the same order as they were issued from that processor. But stores performed by different processors may be seen in a different order by different processors. In this consistency model, only the store order needs to be consistent not the load and that is why it is named as pipelined. PRAM Consistency is easy to implement. The model simply says that there are no guarantees about the order in which different processors see the stores, except that two or more stores performed by the single processor must arrive in order, as if they were in a pipeline. | ||
This model is weaker than Processor Consistency in the sense that it allows to see the stores by different processors in any order even if the store is performed on same memory location. In case of Processor Consistency, cache coherence also works thus store operations performed by different processors on the same location are required to be seen in the same ordered they are issued. | This model is weaker than Processor Consistency in the sense that it allows to see the stores by different processors in any order even if the store is performed on same memory location. In case of Processor Consistency, cache coherence also works thus store operations performed by different processors on the same location are required to be seen in the same ordered they are issued. | ||
''Figure 7'' shows w(x)1 performed by processor P1 and w(x)2 performed by processor P2 are seen in different order by processor P3 and P4 which is not allowed in Processor Consistency as both the stores are performed on same memory location ''x''. | ''Figure 7'' shows that w(x)1 performed by processor P1 and w(x)2 performed by processor P2 are seen in different order by processor P3 and P4 which is not allowed in Processor Consistency as both the stores are performed on same memory location ''x''. | ||
===Weak Ordering Model=== | ===Weak Ordering Model=== | ||
When a programmer writes a program then | When a programmer writes a program then he makes sure that the ordering issue is addressed in the program using synchronization primitives. So it can be said that a majority of the programs are properly synchronized. These synchronization primitives can be of the form of barriers, point-to-point synchronization, lock etc. Also, it can be concluded that if a program is properly synchronized, there is no data race that can occur. '''Data race''' is defined as the simultaneous access of a single location by multiple threads in which at least one of the access is a store. Simultaneous loads do not change the outcome of the loads hence they cannot produce data race. However, simultaneous stores may overwrite each other hence they can induce data race. A simultaneous load and store also may cause the load to return different values. The implication of the lack of data race in a properly synchronized program is that the ordering of memory accesses can be relaxed except at synchronization points. This concept is implemented in [http://en.wikipedia.org/wiki/Weak_consistency Weak Ordering Consistency Model]. The Weak Ordering model uses two assumptions, | ||
[[Image:MCM_WO.png|thumbnail|right|400px|Figure 8: Representation of Order of any Load or Store in Weak Ordering<sup><span id="3body"></span></sup>]] | [[Image:MCM_WO.png|thumbnail|right|400px|Figure 8: Representation of Order of any Load or Store in Weak Ordering<sup><span id="3body"></span></sup>]] | ||
| Line 174: | Line 174: | ||
* All loads, stores and synchronization accesses following it must not have issued. | * All loads, stores and synchronization accesses following it must not have issued. | ||
In the ''Figure 8'', S represents the synchronization access point. As the Weak Ordering | In the ''Figure 8'', S represents the synchronization access point. As the Weak Ordering model says that the ordering of the memory accesses can be relaxed between the synchronization access points thus the store w(x)1 and w(x)2 performed by processor P1 can be seen in a different order by processor P2 and P3 as long as the synchronization point has not reached. If the load r(x)1 and r(x)2 are performed after the synchronization point then all the loads performed by different processors must see the latest stores. | ||
=====Basic Implementation of Weak Ordering Model ===== | =====Basic Implementation of Weak Ordering Model ===== | ||
When a synchronization access is encountered at the processor pipeline, first of all, all the memory accesses following this synchronization point are flushed out of the processor pipeline. Then this synchronization access itself is made to halt until all the memory accesses before this synchronization point are completed. All the loads have obtained their value and all the stores have propagated their values. | When a synchronization access is encountered at the processor pipeline, first of all, all the memory accesses following this synchronization point are flushed out of the processor pipeline. Then this synchronization access itself is made to halt until all the memory accesses before this synchronization point are completed. All the loads have obtained their value and all the stores have propagated their values. | ||
Weak Ordering is more relaxed than Processor Consistency because a Weak Ordering compiler can reorder the memory accesses and it just have to make sure that they do not cross the synchronization points. In Processor Consistency only Store -> Load access is relaxed. This model works well if the critical section is big containing more memory accesses to be executed. If the critical section is small then there are very less opportunities to reorder the memory accesses, as there are less number of them. So when critical section is small then Processor Consistency | Weak Ordering is more relaxed than Processor Consistency because a Weak Ordering compiler can reorder the memory accesses and it just have to make sure that they do not cross the synchronization points. In Processor Consistency only Store -> Load access is relaxed. This model works well if the critical section is big containing more memory accesses to be executed. If the critical section is small then there are very less opportunities to reorder the memory accesses, as there are less number of them. So when critical section is small then Processor Consistency model does better than Weak Ordering model. Weak Ordering model is more relaxed but its program complexity is higher than Processor Consistency. | ||
===Release Consistency Model=== | ===Release Consistency Model=== | ||
| Line 197: | Line 197: | ||
=====Basic Implementation of Release Consistency Model ===== | =====Basic Implementation of Release Consistency Model ===== | ||
The release synchronization must prevent downward migration, so when a release synchronization access is encountered in the processor pipeline, the release access is halted until all prior memory accesses have completed. An acquire synchronization must prevent upward migration. When an acquire synchronization access is encountered in the processor pipeline, all instructions younger than it (including all loads and stores) are canceled and re-executed after the acquire synchronization completes. Similar to Weak Ordering, Release Consistency allows the compiler to freely recorder loads and stores except that they cannot migrate upward past as acquire synchronization and cannot migrate downward past a release synchronization. Thus overlapping of critical section is allowed in Weak Ordering which is not allowed in Release | The release synchronization must prevent downward migration, so when a release synchronization access is encountered in the processor pipeline, the release access is halted until all prior memory accesses have completed. An acquire synchronization must prevent upward migration. When an acquire synchronization access is encountered in the processor pipeline, all instructions younger than it (including all loads and stores) are canceled and re-executed after the acquire synchronization completes. Similar to Weak Ordering, Release Consistency allows the compiler to freely recorder loads and stores except that they cannot migrate upward past as acquire synchronization and cannot migrate downward past a release synchronization. Thus overlapping of critical section is allowed in Weak Ordering which is not allowed in Release Consistency hence this model is weaker than Release Consistency although Weak Ordering has higher programming complexity than Release Consistency. | ||
''Figure 10'' shows that when processor P1 enters critical section by acquiring lock (A(L)), it performs two stores and then it exits the critical section by releasing the lock (Q(L)). Since processor P2 also uses the same critical section thus it reads the latest value of store by processor P1. As processor P3 does not use the critical section thus it does not matter which value it reads. | |||
===Lazy Release Consistency Model=== | ===Lazy Release Consistency Model=== | ||
Latest revision as of 02:59, 24 March 2015
Previous Page: http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2013/7a_bs
Current Page: http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2015/7a_ap
Memory Consistency
Memory consistency deals with the ordering of all memory operations/accesses (loads and stores) to different memory locations. It can be summarized as the rule which must be enforced among all loads and stores to different locations in a shared memory by different processors. It can also be present in systems without caches.
Memory Consistency Model
In order to maintain memory consistency <ref>http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=546611&url=http%3A%2F%2Fieeexplore.ieee.org%2Fstamp%2Fstamp.jsp%3Ftp%3D%26arnumber%3D546611</ref><ref>http://www1.ece.neu.edu/~jmankin/docs/jmankin_mem_const.pdf</ref> in a multiprocessor system, when a program is executed on it, a model is required to specify the behavior of how the memory has to be accessed or to provide an agreement between the memory implementation and the program which is going to utilize this memory. This model is called Memory Consistency Mode and it is used to define the ordering in which all loads and stores must be performed, both relative to each other in the same program and to other loads and stores by another program on another processor. The programmer before writing the code must have knowledge of the Memory Consistency Model used by the hardware in order to ensure program correctness. The code below from Solihin<ref>Yan Solihin. "Fundamentals of Parallel Computer Architecture: Multi-chip and Multicore Systems." Solihin Publishing & Consulting LLC, 2009.</ref> shows an example of possible inconsistency:
P0 P1
S1 : datum = 5 S3 : while(!datumIsReady) {}
S2 : datumIsReady = 1 S4 : print datum
In this example, P0 sets the values of datum and datumIsReady to 5 and 1 respectively. By setting datumIsReady to 1, P0 signals P1 that datum is now ready. P1 spins in the while loop waiting for this flag to become 1 and then prints datum. In this example and in similar cases, it is important that the compiler understands what the programmer has intended so that the program order is preserved. Within a uni-processor, declaring which variables must be synchronized can solve this problem. For instance when using C, this can be accomplished by declaring variables that may be susceptible to inconsistency as volatile.
When a programmer writes a code, then he implicitly expects that the order of all memory accesses (loads and stores) coming out of a processor will be performed in the program order and each memory access will be performed atomically. The code below from Solihin shows another example of possible inconsistency:
P0 P1 P3
S1 : x = 5 S3 : while(!xReady) {} S6: while(!xyReady)
S2 : xReady = 1 S4 : y = x + 4 S7: z = x * y
S5 : xyReady = 1
In this example, initially, the values of x, y, z, xReady and xyReady are zero. Consider that the code when executed follows program program order that is S1 -> S2 -> S3 -> S4 -> S5 -> S6 -> S7.
So as per the code, firstly P0 executes its statements S1 and S2 in order and sets their values as 5 and 1 respectively. P1 receives the signal 1 from P0 and comes out of the loop in S3. P1 then reads the value of x and sets the value of y and xyReady as 9 and 1 respectively. P3 then receives the signal xyReady as 1 so it reads the value of x and y and sets the value of z. The programmer expects that the value of z should be 45 (5*9) due to the atomicity of the execution of instructions.
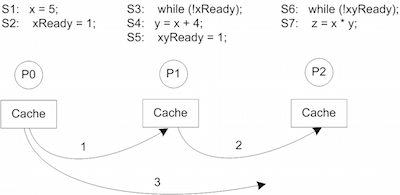
Now, consider the scenario given in Figure 1. P0 executes S1, which writes a value of 5 to x. This write is then propagated to P1 and P2, however it reaches P1 faster than P2. Then, P0 performs a write to xReady, which is also propagated to P1. P1 now sees the new values of xReady and x. So P1 executes its S4 statement, assigning a value of 9 to y, and then sets xyReady to 1 which is propagated to P2. P2 then comes out of its loop and reads the value of x and y. Since the value of x from P0 has yet not reached P2, P2 reads a fresh value of y but the stale value of x. Thus the output of the program is unexpected which in this case is z = 0.
From the first and second example it is clear that the implicit expectation of a programmer is:
- Memory accesses performed by a single processor should be occurred in program order and
- Each of them should be performed atomically.
Such an expectation is defined as Sequential Consistency.
Memory Semantics in Uniprocessor Systems
Uniprocessor languages use simple sequential semantics for memory operations, which allow the programmer to assume that all memory operations will occur one at a time in the sequential order specified by the program. Thus, the programmer can expect a load to return the value of the most recent store to the location according to sequential program order. It is sufficient to only maintain uniprocessor data and control dependences. The compiler and hardware can freely reorder operations to different locations if the uniprocessor data and control dependences are respected. This enables compiler optimizations such as register allocation, code motion, loop transformations and hardware optimizations such as pipelining, multiple issue, write buffer bypassing and forwarding, and lockup-free caches, all of which lead to overlapping and reordering of memory operations.<ref>Sarita V. Adve. Kourosh Gharachorloo. "Shared Memory. Consistency Models: A Tutorial." Digital Western Research Laboratory 250 University Avenue Palo Alto. <http://www.hpl.hp.com/techreports/Compaq-DEC/WRL-95-7.pdf</ref><ref>http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2013/7a_bs</ref>
Memory Semantics in Multiprocessor Systems
Unfortunately, memory consistency is not as straightforward on multiprocessors. With regard to the examples above, instead of each process running on a separate thread, each process runs on a separate processor. With multiple processors, more problems arise with respect to order of execution. While one process might execute instructions in program order, other processes may not recognize the executions in the same order due to delays in communication. How processors handle this problem depends on the chosen consistency model <ref>http://www-vs.informatik.uni-ulm.de/teach/ss05/dsm/arizona.pdf</ref><ref>http://www.cs.columbia.edu/~Roxana/teaching/DistributedSystemsF12/lectures/lec12.pdf</ref>.
Types of Memory Consistency Models
Following Tree (Figure 2) shows different Memory Consistency models according to their weakening order. A model is said to be weaker compared to another model if it has less restrictions.
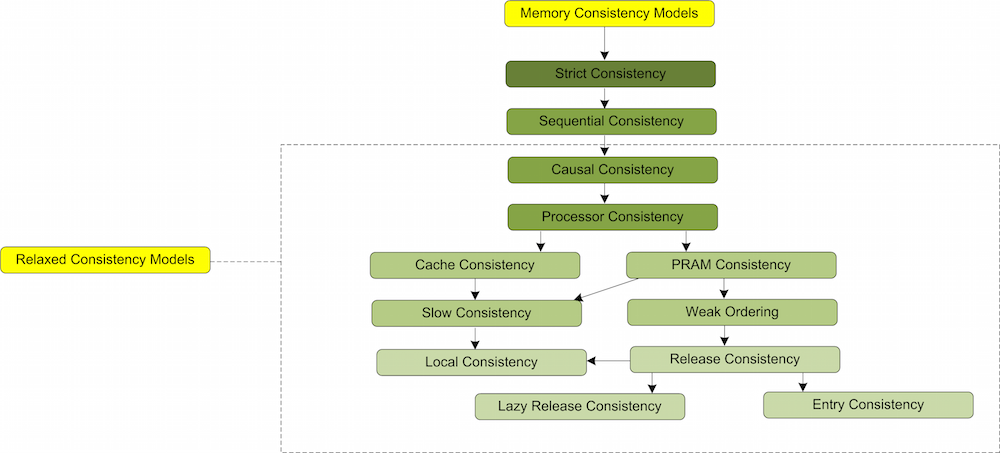
The tree represents most of the memory consistency models. There are some other memory consistency models as well, which are listed as follows.
- Delta Consistency Model
- Eventual Consistency Model
- Fork Consistency Model
- One-Copy Serializability
- Vector-Field Consistency Model
Following are the detailed explanations of different consistency models<ref>http://en.wikipedia.org/wiki/Consistency_model</ref>:
Strict Consistency Model
Strict Consistency Model is the strictest of all consistency models. It is stated as any load to a memory location returns the latest value stored to this memory location. This model implicitly assumes all store operations are propagated almost instantaneously to the other processors in the system. If a value stored at a memory location is changed then all the loads to that location will give the latest value of the store.
Sequential Consistency Model
The most commonly assumed memory consistency model for shared memory multiprocessors is Sequential Consistency Model <ref>http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1675439&tag</ref>. This model is similar to Atomic Consistency but it contains the possibility of optimizations to improve the performance. Sequential Consistency was formally defined by Lamport <ref>http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1675439</ref> as follows:
“A multiprocessor system is sequentially consistent if the result of any execution is the same as if the operations of all the processors were executed in some sequential order, and the operations of each individual processor appear in this sequence in the order specified by its program.”
There are two main aspects to sequential consistency:
- Maintenance of the program order among memory operations from individual processors
- Maintenance of a single sequential order among memory operations from all processors
The second aspect makes it appear as if one memory operation executes atomically or instantaneously with respect to other memory operations. This model is weaker than Strict Consistency model as this model does not require all changes to be propagated instantaneously to all the other processors in the system.
Figure 4 represents how the different loads and stores are performed when Sequential Consistency Model is used in the hardware. P1 stores a value “a” then P2 stores a value “b”. P3 reads the value stored by P1 then P4 reads the value stored by P2 and so on. At each time, a single memory access operation is performed. Both P3 and P4 read the values stored by P1 and P2 in the proper order as they are propagated.
Basic Implementation of Sequential Consistency
The basic implementation of SC involves execution of one memory access at a time without overlapping it with another memory access. Thus it is required to understand the starting and ending point of a particular memory access. Memory accesses are performed when either there is a load or a store operation: Consider a load operation. A load operation is completed in below four steps:

- Step 1: Computation of effective address in a functional unit.
- Step 2: Cache access to the effective address issued by memory hierarchy.
- Step 3: Fetching the data value associated with the address.
- Step 4: Returning the value to the destination register of the load instruction.
Here, it is clear that Step 1 and Step 4 are not affected by other memory accesses. Effective address (Step 1) is computed in the functional unit which involves computation not access. Similarly the final value to be loaded in the destination register (Step 4) has already been fetched from the cache so it does not involve any further memory access. Thus, it can be concluded that the actual load (which involves memory access) starts from Step 2 and ends on Step 3. These two steps should be performed atomically.
Consider a store operation. A store operation is completed in below four steps:
- Step 1: Computation of effective address in a functional unit.
- Step 2: The store is committed by copying the destination address and the latest value to be stored to a write buffer.
- Step 3: The store value in the write buffer is released to the cache.
- Step 4: The store is considered complete when this new value is fully propagated to the other processors.
As the store involves multiple cache values thus effectively the store starts when the destination address is issued and the latest value is stored in the write buffer in Step 2 till Step 4 where the store is fully propagated to other caches. So these steps should be performed atomically. It can be concluded that the basic implementation of SC inflicts a lot of restrictions on how the instructions within a program have to be executed and thus it affects the performance. So in order to improve the performance of SC, few optimizations in the model are possible.
Techniques to improve Sequential Consistency performance
Performance of a Sequential Consistency model can be improved if the execution of memory accesses is made faster and when it is allowed for the memory accesses to be overlapped with respect to one another as listed below,
- The first performance enhancement technique avoids the overlapping of execution of loads and stores but involves overlapping of the data fetches that are generated by these loads and stores. In this technique, load/store prefetching is performed on the data which is to be used in the coming load/store by changing the state of the cache block to S (load prefetching) or M (store prefetching). Thus when the actual load/store memory access is performed then it takes less time to complete.
- The second technique of performance enhancement depends on speculation access where the execution of a load can be overlapped with the execution of the older load by speculatively assuming that the older load is executed atomically. If the older load does not get executed atomically then this younger load is canceled and it is executed again. This speculative execution is typically only implemented for loads. All stores are issued to the cache atomically only.
Relaxed Consistency Models
These models basically loosen up the memory access restrictions of Sequential Consistency model. As these models do not put a lot of restriction on the sequence of the memory accesses thus their performance is better than Sequential Consistency model. But the implementations of these models require a lot of complexity in the program. During coding, the programmers have to make sure that their programs obey the rules of the consistency model that the hardware provides.
Relaxation in the memory accesses may allow the order of execution of the instructions in a program different from the programmer’s expectation. Thus to prevent any non-deterministic outcome of the program, safety net is provided to the programmers to implement it in their programs to specify strict ordering between a pair of memory accesses. This safety net is provided in terms of fence instruction. Once a fence instruction is implemented in the program then it prohibits all the memory accesses following it until all the memory accesses before it have been completed. Fence instruction is of two types. When the fence is only applied to the stores such that there is a proper ordering of the memory accesses between all the stores before the fence and all following it then such type of fence is called store fence/barrier. On the other side, when the fence is only applied to the loads such that there should be perfect ordering between the loads before the fence appears and the loads after the fence then such a fence is called load fence/barrier.

When a fence is implemented in the program then all the memory accesses younger than fence are flushed out from the pipeline. Firstly all the memory accesses older than fence are completed and then the processor state is restored to the state prior to the fence instruction and execution is resumed from that point.
Causal Consistency Model
Causal Consistency Model <ref>http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.50.3356</ref> is a weaker model of Sequential Consistency model. Here, a differentiation is made between events that are potentially causally connected with each other and those that are not. A system provides Causal Consistency if memory operations that potentially are causally related are seen by every processor of the system in the same order. Operations that are not causally related are said to be concurrent. Concurrent writes may be seen in different order by different processors but Condition-writes (i.e. ones that are potentially causally related) must be seen by all processors in the same order. Causal Consistency model is weaker than Sequential Consistency model in the sense that all the concurrent writes in this model can be seen in any order by all the other processors in the system while they are required to be seen in the same order by other processors in Sequential Consistency.
When a store operation follows a load operation performed by a processor then the load and store are considered causally connected. Similarly, when a load operation follows a store operation then it is also considered causally connected. Also, the transitive closure of the previous two types of pairs of operations are also causally related.
Figure 5 shows an order of loads and stores in this model. Store operation w(x)1 by processor P1 is causally related to store operation w(x)2 by processor P2 but the store operations w(x)3 by processor P1 and w(x)2 by processor P2 are concurrent writes thus can be seen in any order by processor P3 and P4.
Processor Consistency Model

Processor Consistency model is a weaker model than Causal Consistency. In Sequential Consistency a proper ordering is forced on all the memory accesses, which are, Load -> Load, Load -> Store, Store -> Store, and Store -> Load. The basic implementation of a Processor Consistency Model is based on relaxing the ordering between an older store and a younger store (Store -> Load). In this model, when a store has not completed, a younger load is allowed to issue to the cache and even complete. The importance of this is that store instructions can be queued in the write buffer and be completed at a later time without the use of load speculation. In the mean time, loads do not require to wait for the older stores to complete and can access the cache and hence they reduce the load latency. In case of Processor Consistency, when a load is issued to the cache then it is not rolled back even if the illusion of atomicity is broken in contrast to SC where the load is rolled back at once. This result is better performance of Processor Consistency as compared to Sequential Consistency. Processor Consistency only relaxes one ordering rule out of four, hence it only affects the correctness of code that has a store followed by a load. If a program is a properly synchronized program, PC provides the same outcome as Sequential Consistency. In a post and wait synchronization in which a processor produces a data value and sets a flag to signal the availability of the new value. This involves at least two store instructions, which are ordered with respect to each other in Processor Consistency. Once the consumer sees the flag high, it performs at least two loads and this ordering is also guaranteed under Processor Consistency. Thus, post and wait sync produces the same outcome in Processor Consistency as in Sequential Consistency.
Processor Consistency model is weaker than Causal Consistency model in the sense that it requires all the stores performed by a single processor to be seen in the same order by different processors in the system as they are issued but stores performed by the different processors can be seen in any order by other processors in the system while in Causal Consistency all causally related stores are required to be seen in the same order by all the processors. Some definitions of Processor Consistency model involve the concept of cache coherence thus if there are two different stores performed by two different processors on the same memory location then the model requires that these stores are to be seen in the same order by the different processors in the system as they are issued. Figure 6 represents the same concept. Two stores w(x)1 and w(x)2 are performed by two different processors P1 and P2 but as they are performed on the same memory location thus the same order is required to be seen by processor P3 and P4.
PRAM Consistency Model

PRAM Consistency Model <ref>http://cs.gmu.edu/cne/modules/dsm/orange/pram_con.html</ref> <ref>http://www.e-reading.link/chapter.php/143358/220/Tanenbaum_-_Distributed_operating_systems.html</ref>is pipelined random access memory consistency. It is also known as FIFO consistency. This consistency model is even more relaxed than Processor Consistency model. In this model, all processors see the stores performed by one processor in the same order as they were issued from that processor. But stores performed by different processors may be seen in a different order by different processors. In this consistency model, only the store order needs to be consistent not the load and that is why it is named as pipelined. PRAM Consistency is easy to implement. The model simply says that there are no guarantees about the order in which different processors see the stores, except that two or more stores performed by the single processor must arrive in order, as if they were in a pipeline. This model is weaker than Processor Consistency in the sense that it allows to see the stores by different processors in any order even if the store is performed on same memory location. In case of Processor Consistency, cache coherence also works thus store operations performed by different processors on the same location are required to be seen in the same ordered they are issued.
Figure 7 shows that w(x)1 performed by processor P1 and w(x)2 performed by processor P2 are seen in different order by processor P3 and P4 which is not allowed in Processor Consistency as both the stores are performed on same memory location x.
Weak Ordering Model
When a programmer writes a program then he makes sure that the ordering issue is addressed in the program using synchronization primitives. So it can be said that a majority of the programs are properly synchronized. These synchronization primitives can be of the form of barriers, point-to-point synchronization, lock etc. Also, it can be concluded that if a program is properly synchronized, there is no data race that can occur. Data race is defined as the simultaneous access of a single location by multiple threads in which at least one of the access is a store. Simultaneous loads do not change the outcome of the loads hence they cannot produce data race. However, simultaneous stores may overwrite each other hence they can induce data race. A simultaneous load and store also may cause the load to return different values. The implication of the lack of data race in a properly synchronized program is that the ordering of memory accesses can be relaxed except at synchronization points. This concept is implemented in Weak Ordering Consistency Model. The Weak Ordering model uses two assumptions,

- Programs are properly synchronized.
- Programmers correctly express to the hardware, which loads and stores act as synchronization accesses.
Based on the assumptions, the correct behavior of a synchronization access can be defined as:
- Before a synchronization access can issue, all prior loads, stores and synchronization accesses must have completed
- All loads, stores and synchronization accesses following it must not have issued.
In the Figure 8, S represents the synchronization access point. As the Weak Ordering model says that the ordering of the memory accesses can be relaxed between the synchronization access points thus the store w(x)1 and w(x)2 performed by processor P1 can be seen in a different order by processor P2 and P3 as long as the synchronization point has not reached. If the load r(x)1 and r(x)2 are performed after the synchronization point then all the loads performed by different processors must see the latest stores.
Basic Implementation of Weak Ordering Model
When a synchronization access is encountered at the processor pipeline, first of all, all the memory accesses following this synchronization point are flushed out of the processor pipeline. Then this synchronization access itself is made to halt until all the memory accesses before this synchronization point are completed. All the loads have obtained their value and all the stores have propagated their values. Weak Ordering is more relaxed than Processor Consistency because a Weak Ordering compiler can reorder the memory accesses and it just have to make sure that they do not cross the synchronization points. In Processor Consistency only Store -> Load access is relaxed. This model works well if the critical section is big containing more memory accesses to be executed. If the critical section is small then there are very less opportunities to reorder the memory accesses, as there are less number of them. So when critical section is small then Processor Consistency model does better than Weak Ordering model. Weak Ordering model is more relaxed but its program complexity is higher than Processor Consistency.
Release Consistency Model

The Release Consistency model <ref>http://dl.acm.org/citation.cfm?id=139676 </ref> implementation is based on two different types of synchronization accesses:
Acquire synchronization (lock): which ensures that no younger load/store executes before the acquire is complete. Thus it prevents upward migration of memory accesses but not downward migration.
Release synchronization (unlock): which ensures that all older loads/stores complete before the release is issued. This it prevents downward migration of memory accesses but no upward migration.
It is also made sure that acquires and releases must execute atomically with respect to one another. This implies that they must not appear to have overlapped their execution with respect of one another. This model requires all synchronization accesses in a program to be identified correctly and completely, so that the hardware can ensure correct execution of properly synchronized program.
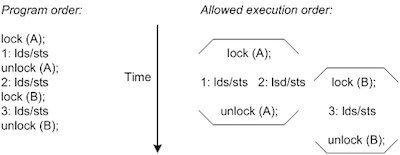
In Figure 9, the synchronization access lock (A) operation prevents upward migration but allows downward migration. The synchronization access unlock (A) operation prevents downward operation but allows upward migration. Due to this, the operation lock (B) can be moved upward. But as in WO, all synchronization accesses are never overlapped, thus lock (A), lock (B), unlock (A) and unlock (B) are not overlapped. Thus, in brief it can be said that WO allows overlapping of critical sections.
Basic Implementation of Release Consistency Model
The release synchronization must prevent downward migration, so when a release synchronization access is encountered in the processor pipeline, the release access is halted until all prior memory accesses have completed. An acquire synchronization must prevent upward migration. When an acquire synchronization access is encountered in the processor pipeline, all instructions younger than it (including all loads and stores) are canceled and re-executed after the acquire synchronization completes. Similar to Weak Ordering, Release Consistency allows the compiler to freely recorder loads and stores except that they cannot migrate upward past as acquire synchronization and cannot migrate downward past a release synchronization. Thus overlapping of critical section is allowed in Weak Ordering which is not allowed in Release Consistency hence this model is weaker than Release Consistency although Weak Ordering has higher programming complexity than Release Consistency.
Figure 10 shows that when processor P1 enters critical section by acquiring lock (A(L)), it performs two stores and then it exits the critical section by releasing the lock (Q(L)). Since processor P2 also uses the same critical section thus it reads the latest value of store by processor P1. As processor P3 does not use the critical section thus it does not matter which value it reads.
Lazy Release Consistency Model
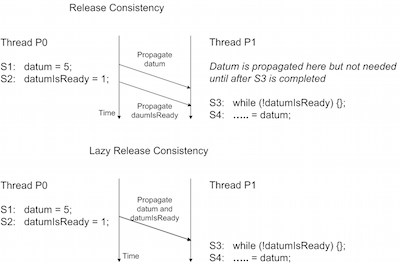
The Lazy Release Consistency model is a further optimization of the Release Consistency model (RC) in which it is considered that the thread that executes an acquire synchronization does not need values written by another thread until the acquire synchronization is completed. When a store is executed in a critical section, then before the unlock is executed, it is made sure that the memory access is propagated fully to the other caches. Then the unlock operation is executed, which involves another store where the value of lockvar is changed to 0. This value is again propagated fully to other caches and then after that the lock operation is executed. It can be concluded that the value of the store in the first critical section is not required until the lock operation for the second critical section is executed. So it can be said that the propagation of the values written prior to the release synchronization can be delayed until the release synchronization is complete and then both the values written in the critical section and on release synchronization can be propagated together to the other caches. This model is beneficial in the cases where there is a little bandwidth available between the processors or in a system where there are high overheads due to the propagation of small amount of data or infrequent propagation of large amount of data.
As shown in the Figure 11, for Lazy Release Consistency, the writes from statements S1 and S2 are combined together and then propagated once S2 is complete.
Entry Consistency Model
Entry Consistency Model <ref>http://cs.gmu.edu/cne/modules/dsm/orange/entry_con.html</ref> is similar to Release Consistency Model as this model also requires the programmer to use acquire and release synchronization accesses at the start and end of each critical section but this model also requires each ordinary shared variable to be associated with some synchronization variable such as a lock or barrier. When an acquire synchronization is done on a variable then only those ordinary shared variables which are guarded by acquire are made consistent. Entry Consistency model is distinguished from Lazy Release Consistency such that Lazy Release Consistency does not associate ordinary shared variables with lock or barrier synchronization accesses.
Cache Consistency Model
Cache Consistency is dealt using cache coherence protocols. This model simply requires that all store operations to the same memory location by the processors be performed in some sequential order. Also, the appearance of their order to other processors is same as the order in which they are performed.
Slow Consistency Model

Slow Consistency Model <ref>http://es.cs.uni-kl.de/publications/datarsg/Senf13.pdf</ref> is weaker than PRAM Consistency Model. This model states that when a load operation is performed on a memory location then the memory returns the latest write operation performed on it. But succeeding loads to the same location may not return stores issued earlier (by the processor that issued the earlier stores) than the first load.
In Figure 12, processor P1 stores 1 at a location x and then stores 1 at another location y. When P2 loads immediately after P1 store for location y, it reads the value 1. However, P2 reads 0 from location x even if location x was written before location y.
Local Consistency Model
Local Consistency Model is considered to be the weakest model. The model requires that all the load and store operations performed by a processor are appeared to that processor as if they are performed on a single processor system. Although, there is no restriction on how the order of memory operations performed by different processors will appear to different processors.
Other Consistency Models
Delta Consistency Model
Delta Consistency Model <ref>https://www.ietf.org/proceedings/50/slides/webi-1/tsld006.htm</ref>states that once a store operation is performed on a memory location then the write propagation of this newly written value takes a fixed time period (delta) after which a load operation of this value at any processor will be consistent to the value at the original processor. In other words, if the load operation of this value is performed at any other processor different from the processor which performs the latest store before a fixed amount of time period the value of the load will not be consistent with the latest value of store. After a fixed amount of time, when the write is fully propagated then all the loads to this location from any processor will be consistent.
Eventual Consistency Model
Eventual Consistency Model <ref>http://dl.acm.org/citation.cfm?doid=2460276.2462076</ref>states that when a sufficient amount of time is given to a change to propagate to all the processors and it is assumed that no other update has been made on this data item then this change is propagated fully to the whole system and any load to this data items returns a consistent result.
Fork Consistency Model
Fork Consistency Model <ref>https://www.usenix.org/legacy/event/osdi04/tech/full_papers/li_j/li_j.pdf</ref> states that if a store operation is performed by an un-trusted processor, then there is a possibility this the store operation by this processor is hidden from the other processors. Similarly if other processors perform any store operations then those values will be hidden from this processor. Thus, effectively they fork the views of them. This is the strongest consistency model that can be achieved with an untrusted server.
One-Copy Consistency Model
One-Copy Consistency Model <ref>https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=0CCwQFjAC&url=http%3A%2F%2Fdb.csail.mit.edu%2Fnedbday13%2Fslides%2Fbernstein.ppsx&ei=tBIOVfyMAompNqG2g9AB&usg=AFQjCNHrRyhJ5_TK28OPEoolWC-af7dXOQ&sig2=I-ffZF0vXUxP2rXbNDCDuw</ref> is the same as sequential consistency, as though there is only one copy of the file, thus, access requests are fully serialized.
Vector-Field Consistency Model
Vector-Field Consistency Model <ref>http://www.gsd.inesc-id.pt/~pjpf/middleware07vector.pdf</ref> is a consistency model for replicated data. It is designed to allow bounded divergence of object replicas. In this model replica consistency is selectively and dynamically strengthened or weakened based on the on-going game state and simultaneously it manages: how the consistency degree is changed throughout the execution; and how the consistency requirements are specified.
Memory Consistency Models Supported by Real Multiprocessors
Strict memory consistency models are easy to implement compared to weaker models with a trade-off in performance. Moreover, weaker models impose a restriction on programmers to handle synchronization. However, weaker models are more desired because of their added performance improvement. One of the challenges faced by multiprocessor makers is to support backward compatibility as they move to newer and weaker models so that the legacy codes are not broken. They generally do this by consulting with OS makers, C and Java experts.
Essentially, memory consistency deals with ordering loads and stores to different memory locations. Different models have different restrictions on ordering. For example, Sequential Consistency Model required all loads and stores in order, while Relaxed Consistency Models allow some type of reordering. Weaker models allow arbitrary reordering, limited only by explicit memory barriers.
Figure 13 <ref>http://www.ai.mit.edu/projects/aries/papers/consistency/computer_29_12_dec1996_p66.pdf</ref> shows ordering relaxation employed in different consistency models along with the safety nets.
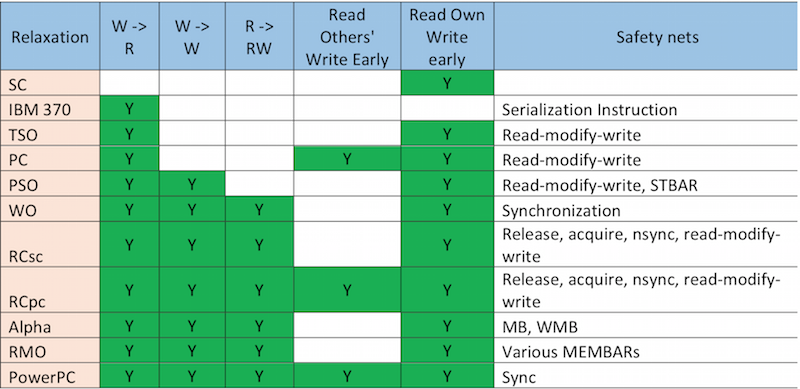
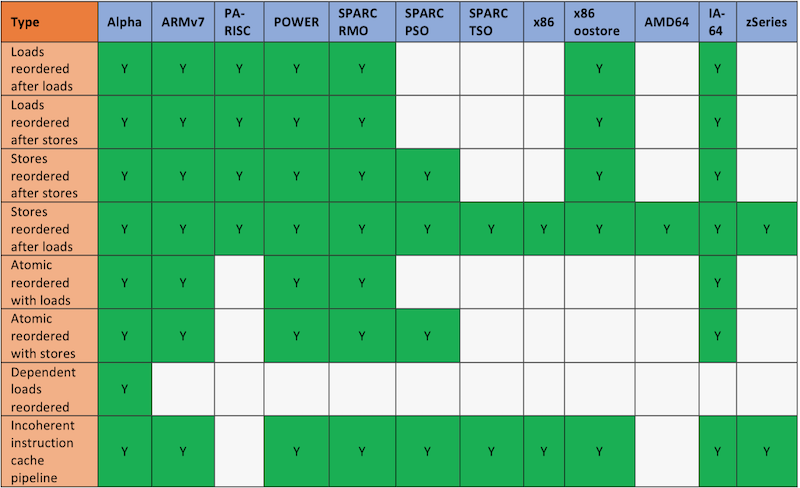
Figure14 <ref>http://www.rdrop.com/users/paulmck/scalability/paper/ordering.2007.09.19a.pdf</ref> shows different relaxation employed on Sequential Consistency Model by various Processors.
Few important processors and their supported memory consistency models are as follows <ref>http://www.linuxjournal.com/article/8212?page=0,1</ref>,
- Alpha
Alpha uses weakest consistency model facilitating all kinds of memory ordering. Because of its most aggressive memory reordering, it has defined the Linux kernel memory-ordering primitives that must work on all CPUs with stricter memory ordering.
- Intel x86
Some x86 implemented a stronger Consistency models like Total Store Order (TSO). The x86-TSO is based on TSO extended the concept of a global lock. These are still Causal Consistency models <ref> Intel 64 architecture memory ordering white paper, 2007. Intel Corporation. SKU 318147-001</ref>, which allow different processors to see the writes to different locations in different orders.
- AMD64
AMD64 offers slightly stronger memory consistency compared to x86.
- IA64
IA64 offers a weak consistency model. Here, an absence of memory barrier instructions gives IA64 right to arbitrarily reorder memory references.
- SPARK
Solaris on SRAK used TSO ordering, however, 64-bit Linux runs SPARK on Relaxed Memory order. Additionally, SPARK also supports Partial Store Order (PSO).
- PA-RISC
This architecture permits full re-ordering of loads and stored but actual CPUs run fully ordered loads and stores.
- POWER
POWER and POWER-PC CPUs provide many relaxations along with wide variety of memory-barriers like sync, lwsync, eieio, isync.
Additionally, Figure 15 shows some of the other commercial systems providing different relaxations on Sequential Consistency.

References
<References> [1] Yan Solihin. "Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems." Solihin Publishing & Consulting LLC, 2009.
[2] Sarita V. Adve. Kourosh Gharachorloo. "Shared Memory. Consistency Models: A Tutorial." Digital Western Research Laboratory 250 University Avenue Palo Alto. <http://www.hpl.hp.com/techreports/Compaq-DEC/WRL-95-7.pdf>
[3] Kai Li, and Paul Hudak. "Memory coherence in shared virtual memory systems". Published in Journal ACM Transactions on Computer Systems (TOCS), Volume 7 Issue 4, Nov. 1989 <http://dl.acm.org.prox.lib.ncsu.edu/citation.cfm?id=75104.75105&coll=DL&dl=GUIDE&CFID=251927&CFTOKEN=71004880>.
</References>
Quiz
1.What is the major difference between One-Copy Serializability and Sequential consistency?
a) No difference
b) One copy Serializability Model has only one copy of the file.
c) Sequential Consistency Model has only one copy of the file.
d) None.
2.On what basis are memory consistency strategies classified? (More than one option could be correct)
a) Page faults
b) Page synchronization
c) Page ownership
d) None.
3.Which of the following is true about sequential consistency? (More than one option could be correct)
a) All orderings are enforced.
b) Loads and stores can exchange positions freely.
c) Performance can suffer
d) SC is deterministic
Quiz Answers: 1. b 2. b,c 3. a,c