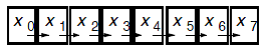CSC/ECE 506 Spring 2015/5a vv: Difference between revisions
| (57 intermediate revisions by 3 users not shown) | |||
| Line 11: | Line 11: | ||
= Introduction to Linked-List Parallel Programming = | = Introduction to Linked-List Parallel Programming = | ||
One component that tends to link together various data structures is their dependence at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket in order to resolve collisions, trees have linked lists with left and right tree node paths, and graphs have linked lists to determine | A [http://en.wikipedia.org/wiki/Linked_list linked list] is a data structure which contains a set of nodes. Nodes in linked list are composed of data and references to next node. It is the simplest form of linked data structures. Other linked data structures include Trees, Hash Tables and Graphs. One component that tends to link together various linked data structures is their dependence at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket in order to resolve collisions, trees have linked lists with left and right tree node paths, and graphs have linked lists to determine the paths. | ||
To understand how parallelization techniques are applied to linked data structures, a copy-scan technique is illustrated in brief, which is further extended to a partial sum computation in a linked list. | |||
For an array processing algorithm, a common technique used at the processor level is the copy-scan technique. This technique involves copying rows of data from one processor to another in a log(n) fashion until all processors have their own copy of that row. From there, you could perform a reduction technique to generate a sum of all the data, all while working in a parallel fashion. Take the following grid: | For an array processing algorithm, a common technique used at the processor level is the copy-scan technique. This technique involves copying rows of data from one processor to another in a log(n) fashion until all processors have their own copy of that row. From there, you could perform a reduction technique to generate a sum of all the data, all while working in a parallel fashion. Take the following grid:<ref>http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html</ref> | ||
The basic process for copy-scan would be to: | The basic process for copy-scan would be to: | ||
# | # In the first step, copy the row 1 elements to corresponding index numbers of row 2 array. | ||
# | # In second step, copy the row 1 elements to corresponding indexes in array of row 3, similarly row 2 elements -> row 4. | ||
# | # In this manner, in the nth step, 2^n rows can copied to 2^n rows | ||
# This can operation is performed until all rows have been copied in a log(n) fashion. | |||
# Perform the parallel operations to generate the desired result (reduction for sum, etc.). | # Perform the parallel operations to generate the desired result (reduction for sum, etc.). | ||
[[File:CopyScan.gif]] | [[File:CopyScan.gif]] | ||
With [http://en.wikipedia.org/wiki/Linked_list linked lists], there is a concept called pointer doubling, which works in a very similar manner to copy-scan.<ref>http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html</ref> | |||
With linked lists, there is a concept called pointer doubling, which works in a very similar manner to copy-scan. | |||
# Each processor will make a copy of the pointer it holds to its neighbor. | # Each processor will make a copy of the pointer it holds to its neighbor. | ||
| Line 34: | Line 33: | ||
# Perform the parallel operations to generate the desired result. | # Perform the parallel operations to generate the desired result. | ||
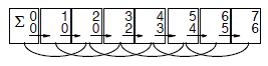
Pointer doubling or [https://en.wikipedia.org/wiki/Pointer_jumping pointer jumping] can be used for performing partial sums of a linked list. This is accomplished by adding the value held by the node with the value stored in the node it is pointing to. This is repeated until all pointers have reached the end of the list. The result is a linked list which contains the sum of the node and all preceding nodes. Below is an example of this algorithm in action. | |||
[[File:PartialSums1.png]] | [[File:PartialSums1.png]] | ||
| Line 44: | Line 43: | ||
[[File:PartialSums4.png]] | [[File:PartialSums4.png]] | ||
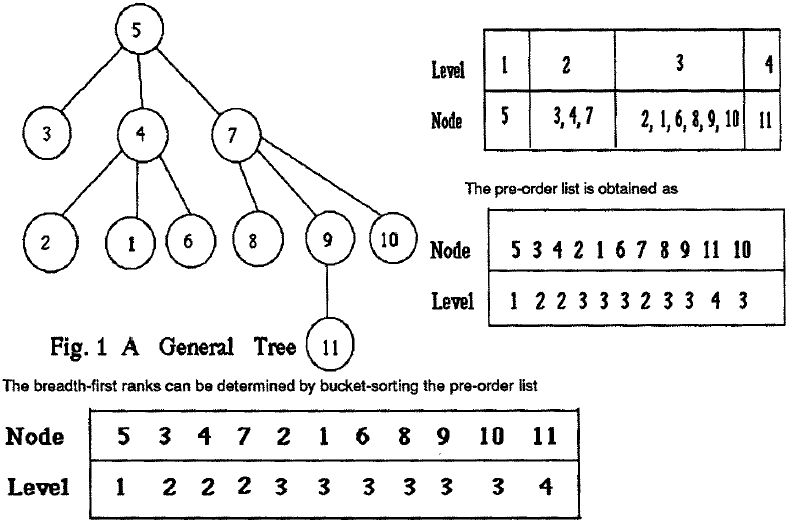
The advantages of pointer | The advantages of pointer jumping<ref>http://en.wikipedia.org/wiki/Pointer_jumping</ref> aren't just for single linked lists. This algorithm can also be used to find the root of a tree (this will be discussed in detail in the later section). The way in which this algorithm is used, is similar to the previous example. Each node will point to the next node until it reaches the end. The result is that every node will have a pointer to the root of the tree. Below diagram shows an example which illustrates the algorithm discussed.<ref>Calvin C.-Y.Chen, Sajal K. Das, "Parallel Breadth-first and Breadth-depth traversals of general trees", Advances in Computing and Information - ICCP '90, ISBN: 978-3-540-46677-2</ref> | ||
[[File:Pointer_Jumping_Example.png]] | [[File:Pointer_Jumping_Example.png]] | ||
<br/> | |||
However, with linked list programming, similar to array-based programming, it becomes imperative to have some sought of locking mechanism or other parallel technique for [http://en.wikipedia.org/wiki/Critical_section critical sections] in order to avoid [http://en.wikipedia.org/wiki/Race_condition race conditions]. To make sure the results are correct, it is important that operations can be serialized appropriately and that data remains current and synchronized. | |||
In this chapter, we will explore parallelization opportunities for hash tables, trees, and graph linked data structures. | |||
In this chapter, we will explore | |||
== Trees == | == Trees == | ||
| Line 56: | Line 55: | ||
=== Introduction to Trees === | === Introduction to Trees === | ||
A tree data structure | A tree data structure <ref>http://en.wikipedia.org/wiki/Tree_%28data_structure</ref> contains a set of ordered nodes with one parent node followed by zero or more child nodes. Typically this tree structure is used with searching or sorting algorithms to achieve log(n) efficiencies. Assuming you have a balanced tree, or a relatively equal set of nodes under each branching structure of the tree, and assuming a proper ordering structure, searches/inserts/deletes should occur far more quickly than having to traverse an entire list. | ||
=== Opportunities for Parallelization === | === Opportunities for Parallelization === | ||
| Line 64: | Line 63: | ||
=== Serial Code Example === | === Serial Code Example === | ||
In this section, we will begin by showing different serial tree traversal | In this section, we will begin by showing different serial tree traversal algorithms<ref>http://en.wikipedia.org/wiki/Tree_traversal</ref> using the tree shown below. | ||
{| | |||
|-valign="top" | |||
| | |||
1 | |||
/ \ | |||
/ \ | |||
/ \ | |||
2 3 | |||
/ \ / | |||
4 5 6 | |||
/ / \ | |||
7 8 9 | |||
The correct output should look like this: | |||
preorder: 1 2 4 7 5 3 6 8 9 | |||
inorder: 7 4 2 5 1 8 6 9 3 | |||
postorder: 7 4 5 2 8 9 6 3 1 | |||
level-order: 1 2 3 4 5 6 7 8 9 | |||
|} | |||
==== Tree Traversal ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Procedure Tree_Traversal is | Procedure Tree_Traversal is | ||
| Line 78: | Line 98: | ||
Data : Integer; | Data : Integer; | ||
end record; | end record; | ||
|} | |||
==== Tree Destroy ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Procedure Destroy_Tree(N : in out Node_Access) is | Procedure Destroy_Tree(N : in out Node_Access) is | ||
| Line 92: | Line 116: | ||
Free(N); | Free(N); | ||
end Destroy_Tree; | end Destroy_Tree; | ||
|} | |||
==== Node Access ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Function Tree(Value : Integer; Left : Node_Access; Right : Node_Access) return Node_Access is | Function Tree(Value : Integer; Left : Node_Access; Right : Node_Access) return Node_Access is | ||
Temp : Node_Access := new Node; | |||
begin | |||
Temp.Data := Value; | |||
Temp.Left := Left; | |||
Temp.Right := Right; | |||
return Temp; | |||
end Tree; | |||
|} | |||
==== Preorder ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Procedure Preorder(N : Node_Access) is | Procedure Preorder(N : Node_Access) is | ||
begin | |||
Put(Integer'Image(N.Data)); | |||
if N.Left /= null then | |||
Preorder(N.Left); | |||
end if; | |||
if N.Right /= null then | |||
Preorder(N.Right); | |||
end if; | |||
end Preorder; | |||
|} | |||
==== Inorder ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Procedure Inorder(N : Node_Access) is | Procedure Inorder(N : Node_Access) is | ||
begin | |||
if N.Left /= null then | |||
Inorder(N.Left); | |||
end if; | |||
Put(Integer'Image(N.Data)); | |||
if N.Right /= null then | |||
Inorder(N.Right); | |||
end if; | |||
end Inorder; | |||
|} | |||
==== Postorder ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Procedure Postorder(N : Node_Access) is | Procedure Postorder(N : Node_Access) is | ||
begin | |||
if N.Left /= null then | |||
Postorder(N.Left); | |||
end if; | |||
if N.Right /= null then | |||
Postorder(N.Right); | |||
end if; | |||
Put(Integer'Image(N.Data)); | |||
end Postorder; | |||
|} | |||
==== Levelorder ==== | |||
{| | |||
|-valign="top" | |||
| | |||
Procedure Levelorder(N : Node_Access) is | Procedure Levelorder(N : Node_Access) is | ||
Package Queues is new Ada.Containers.Doubly_Linked_Lists(Node_Access); | |||
use Queues; | |||
Node_Queue : List; | |||
Next : Node_Access; | |||
begin | |||
Node_Queue.Append(N); | |||
while not Is_Empty(Node_Queue) loop | |||
Next := First_Element(Node_Queue); | |||
Delete_First(Node_Queue); | |||
Put(Integer'Image(Next.Data)); | |||
if Next.Left /= null then | |||
Node_Queue.Append(Next.Left); | |||
end if; | |||
if Next.Right /= null then | |||
Node_Queue.Append(Next.Right); | |||
end if; | |||
end loop; | |||
end Levelorder; | |||
|} | |||
==== main ==== | |||
{| | |||
|-valign="top" | |||
| | |||
N : Node_Access; | |||
N : Node_Access; | begin | ||
N := Tree(1, | |||
Tree(2, | |||
Tree(4, | |||
Tree(7, null, null), | |||
null), | |||
Tree(5, null, null)), | |||
Tree(3, | |||
Tree(6, | |||
Tree(8, null, null), | |||
Tree(9, null, null)), | |||
null)); | |||
Put("preorder: "); | |||
Preorder(N); | |||
New_Line; | |||
Put("inorder: "); | |||
Inorder(N); | |||
New_Line; | |||
Put("postorder: "); | |||
Postorder(N); | |||
New_Line; | |||
Put("level order: "); | |||
Levelorder(N); | |||
New_Line; | |||
Destroy_Tree(N); | |||
end Tree_traversal; | |||
|} | |||
=== Parallel Solution === | === Parallel Solution === | ||
The fact that trees are comprised of independent sub-trees makes parallelizing them | Now that we have seen standard tree traversal techniques, we will look at how tree traversal can be parallelized. Tree is a good candidate to exploit parallelism. Since each node/sub-tree is independent in a binary tree, a large tree can be split up into 2, 4, 8, or more subtrees and each processor holds a sub-tree. In this method, the only data that is common to all processors are the parent nodes of all sub-trees. Consider a perfect balanced binary tree which has k levels. So the total number of nodes in the tree will be equal to 2^k-1. An example of perfect balanced binary tree is shown in the figure below. For the example shown below, four processors are required if each sub-tree labelled Rank 0, Rank 1, Rank 2 and Rank 3 is assigned to a single processor. The three nodes colored in red is the common data shared by all processors.So in this scenario, four processors each have four independent sub-trees and they share three nodes. In general, if n processors each have n independent sub-trees, they share n-1 nodes in common. If the size of the tree was increased and the number of processors was also increased, the number of shared nodes would also increase to support the increased number of sub-trees.<ref>http://www.shodor.org/media/content//petascale/materials/UPModules/Binary_Tree_Traversal/Binary_Tree_Traversal_Module_Document.pdf</ref> | ||
very easy. Properly done, the portion of these traversals that is parallelizable grows | |||
at 2n for an n-generation tree. While the processors only need to synchronize once, at | The fact that trees are comprised of independent sub-trees makes parallelizing them very easy. Properly done, the portion of these traversals that is parallelizable grows at 2n for an n-generation tree. While the processors only need to synchronize once, at the end, the parallelizable portion approaches 100% for large trees (but keep in mind [http://en.wikipedia.org/wiki/Amdahl's_law Amdahl’s Law], footnote 1). The basic steps for parallelizing these traversals are as follows: | ||
the end, the parallelizable portion approaches 100% for large trees (but keep in mind [http://en.wikipedia.org/wiki/Amdahl's_law Amdahl’s Law], | |||
footnote 1). The basic steps for parallelizing these traversals are as follows: | |||
# Perform the traversal on the parent part of the tree. | # Perform the traversal on the parent part of the tree. | ||
| Line 221: | Line 250: | ||
# The processor will return its result that can be used exactly as if it was a serial processor. | # The processor will return its result that can be used exactly as if it was a serial processor. | ||
[[File:parallel_tree.png | [[File:parallel_tree.png]] | ||
A [http://www.cs.bu.edu/teaching/c/tree/breadth-first/ Breadth-First traversal] is somewhat more complicated to implement as a | A [http://www.cs.bu.edu/teaching/c/tree/breadth-first/ Breadth-First traversal] is somewhat more complicated to implement as a parallel system because at each level, it must access nodes from all of the parallel processors. Theoretically, a Breadth-First traversal can achieve complete parallelization of Pre-, In-, and Post-Order traversals. As the degree of parallelism is increased, the speed up increases as per Amdahl's law. One thing to remember in the parllelization though, is that the amount of processor-to-processor data transmission adds in a greater potential for delays, thus slowing | ||
parallel system because at each level, it must access nodes from all of the parallel | down the algorithm. Nevertheless, as the size of the tree increases the size of the generations grows at the rate of 2n while the number of synchronizations grows at a rate of n for an n-generation tree, so the parallelizable portion of these traversals also approaches 100%. The basic steps for parallelizing this traversal are as follows: | ||
processors. Theoretically, a Breadth-First traversal can achieve complete parallelization of Pre-, In-, and Post-Order traversals. As the degree of parallelism is increased, the speed up increases as per Amdahl's law. One thing to remember in the parllelization though, is that the amount of processor-to-processor data transmission adds in a greater potential for delays, thus slowing | |||
down the algorithm. Nevertheless, as the size of the tree increases the size of the | |||
generations grows at the rate of 2n while the number of synchronizations grows at a | |||
rate of n for an n-generation tree, so the parallelizable portion of these traversals | |||
also approaches 100%. The basic steps for parallelizing this traversal are as | |||
follows: | |||
# Perform the traversal on the parent part of the tree. | # Perform the traversal on the parent part of the tree. | ||
| Line 237: | Line 260: | ||
# Allow each processor to execute the next generation of the Breadth-First C algorithm detailed above, and then wait again. | # Allow each processor to execute the next generation of the Breadth-First C algorithm detailed above, and then wait again. | ||
# Repeat Steps 3 and 4 until there are no nodes remaining | # Repeat Steps 3 and 4 until there are no nodes remaining | ||
Here, since each processor is assigned an independent sub-tree, elaborate locks are not required. | Here, since each processor is assigned an independent sub-tree, elaborate locks are not required. | ||
| Line 248: | Line 270: | ||
< | <pre> | ||
Algorithm GEN-COMP-NEXT: | Algorithm GEN-COMP-NEXT: | ||
for all Pi, 1<=i<=n, do | |||
parallel begin | |||
Step 1: Processor Pi builds the jth field of i's parent node if i is the jth child of its parent. The jth field (if it is not the last field) is stored in the ith index of array SUPERNODE. | |||
Step 2: Processor Pi builds node i's last fiend whose array index is (n+1) | |||
parallel end | |||
</ | </pre> | ||
| Line 261: | Line 283: | ||
< | <pre> | ||
Algorithm BF-TRAVERSAL (bfank, level, preorder-list) | Algorithm BF-TRAVERSAL (bfank, level, preorder-list) | ||
Step 1. Divide the preorder-list into p blocks. Each processor builds partial lists from the nodes in the block. The header and the taller arrays for the lists built by processor i are denoted by hd[*,i] and tl[*,i], respectively. | |||
for all Pi, 1<=i<=p do | |||
parbegin | |||
Pi works on nodes pre-order-list[k], where (i-1)*(n/p) <= k < (i*n/p) | |||
Pi initializes list[k] to zreo /* the successor of k-th input in a partial list */ | |||
/* Phase 1. Pi initializes entries in hd[*,i] and tl[*,i] that are used and entries in hdflag */ | |||
hd[level[preorder-list[k]], i] := 0; tl[level[preorder-list[k]], i] := 0; hdflag[k] := 0; | |||
/* Phase 2. Build partial lists */ | |||
Pi adds each of the n/p nodes to the partial list for the level of that node and updates hd[*,i], tl[*, i], and list [*] accordingly. | |||
parend; | |||
Step 2. Link up partial lists. | |||
/* Phase 1. Initialize header and tailer for the global lists */ | |||
for all Pi, 1 <= i <= p, do | |||
initialize head[k] and tail[k] to zero, for (i-1)*n/p <= k < (i*n/p) | |||
P1 sets head[n+1] and tail[n+1] to zero; | |||
/* Phase 2. Link partial lists to form a list for each level */ | |||
for each of the p blocks do | |||
for all Pi, 1 <= i <= p, do /* all processors work on the same block */ | |||
parbegin | |||
for i := 1 to (n/p^2) do | |||
begin | |||
Pi is given at most a node mi in each iteration. | |||
if hdflag[mi] = 1 /* The first element in its partial list */ | |||
then | |||
if the global list for the level of node mi is empty | |||
then | |||
let head[level[mi]] and tail[level[mi]] point to mi | |||
else | |||
list[tail[level[mi]]] := mi and update tail[level[mi]] to be the tail of the partial list for mi. | |||
end; | |||
parend; | |||
Step 3. Create a linked list to implement the NEXT function | |||
for all Pi, 1 <= i <= p, do | |||
parbegin | |||
for k := (i-1)*(n/p)+1 to (i*n/p) do | |||
if(head[k] != 0 and head[k+1] != 0) then list[tail[k]] := head[k+1]; | |||
parend; | |||
Step 4. Obtain ranking | |||
LINKED-LIST-RANKING(list, tmp-rank, n); | |||
Step 5. Output the result | |||
for all Pi, 1 <= i <= p, do | |||
parbegin | |||
</ | for k := (i-1)*(n/p)+1 to (i*n/p) do bfrank[preorder-list[k]] := tmp-rank[k]; | ||
parend; | |||
</pre> | |||
| Line 320: | Line 344: | ||
=== Introduction to Hash Tables === | === Introduction to Hash Tables === | ||
Hash tables | Hash tables<ref>http://www.devjavasoft.org/code/classhashtable.html</ref> are very efficient data structures often used in searching algorithms for fast lookup operations. They are used extensively in data processing as in involves a vast amount of data through the hash table using as few indirection's in the storage structure as possible. | ||
A single hash table level look can easily become a bottleneck, thus several method were developed to overcome this difficulty. Hash tables contain a series of "buckets" that function like indexes into an array, each of which can be accessed directly using their key value. The bucket for which a piece of data will be placed is determine by a special hashing function. | A single hash table level look can easily become a bottleneck, thus several method were developed to overcome this difficulty. Hash tables contain a series of "buckets" that function like indexes into an array, each of which can be accessed directly using their key value. The bucket for which a piece of data will be placed is determine by a special hashing function. | ||
| Line 326: | Line 350: | ||
The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value. | The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value. | ||
In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list. | In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list. <ref>http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg</ref> | ||
There are several parallel implementations of hash tables available that use lock-based synchronization. Larson et al. use two lock levels, there is one global table level lock, and there is one separate lightweight lock (a flag) for each bucket. The high level lock is just used for setting the bucket level flags and released right afterwards. This ensures a fine grained mutual exclusion (concurrent operations on bucket level), but needs only one real lock for the implementation. | There are several parallel implementations of hash tables available that use lock-based synchronization. Larson et al. use two lock levels, there is one global table level lock, and there is one separate lightweight lock (a flag) for each bucket. The high level lock is just used for setting the bucket level flags and released right afterwards. This ensures a fine grained mutual exclusion (concurrent operations on bucket level), but needs only one real lock for the implementation. | ||
| Line 353: | Line 377: | ||
This would, however, involve a good bit of synchronization, as each processor would need to wait in case a lock was being placed on a specific bucket in the cache hashmap. Unfortunately, traditional locking would be a bad solution to this problem as processors need to run very quickly. Having to wait for locks would destroy the application processing time. The need for a non-locking solution is critical to performance. | This would, however, involve a good bit of synchronization, as each processor would need to wait in case a lock was being placed on a specific bucket in the cache hashmap. Unfortunately, traditional locking would be a bad solution to this problem as processors need to run very quickly. Having to wait for locks would destroy the application processing time. The need for a non-locking solution is critical to performance. | ||
In Java, the standard class utilized for hashing is the HashMap | In Java, the standard class utilized for hashing is the HashMap<ref>http://code.wikia.com/wiki/Hashmap</ref> class. This class has a fundamental weakness though in that the entire map requires synchronization prior to each access. This causes a lot of contention and many bottlenecks on a parallel machine. | ||
Below, I will present a Java-based solution to this problem by using a ConcurrentHashMap class. This class only requires a portion of the map to be locked and reads can generally occur with no locking whatsoever. | Below, I will present a Java-based solution to this problem by using a ConcurrentHashMap class. This class only requires a portion of the map to be locked and reads can generally occur with no locking whatsoever. | ||
| Line 359: | Line 383: | ||
=== Serial Code Examples === | === Serial Code Examples === | ||
''' Simple synchronized example to increment a counter.''' | ''' Simple synchronized example to increment a counter.'''<ref>http://www.javamex.com/tutorials/synchronization_concurrency_8_hashmap.shtml</ref> | ||
< | <pre> | ||
private Map<String,Integer> queryCounts = new HashMap<String,Integer>(1000);<br> | private Map<String,Integer> queryCounts = new HashMap<String,Integer>(1000);<br> | ||
private '''synchronized''' void incrementCount(String q) { | private '''synchronized''' void incrementCount(String q) { | ||
Integer cnt = queryCounts.get(q); | |||
if (cnt == null) { | |||
queryCounts.put(q, 1); | |||
} else { | |||
queryCounts.put(q, cnt + 1); | |||
} | |||
} | } | ||
</ | </pre> | ||
The above code was written using an ordinary HashMap data structure. Notice that we use the synchronized keyword here to signify that only one thread can enter this function at any one point in time. With a really large number of threads, however, waiting to enter the synchronized operation could be a major bottleneck. | The above code was written using an ordinary HashMap data structure. Notice that we use the synchronized keyword here to signify that only one thread can enter this function at any one point in time. With a really large number of threads, however, waiting to enter the synchronized operation could be a major bottleneck. | ||
| Line 377: | Line 401: | ||
''' Iterator example for synchronized HashMap.''' | ''' Iterator example for synchronized HashMap.''' | ||
< | <pre> | ||
Map m = Collections.synchronizedMap(new HashMap());<br> | Map m = Collections.synchronizedMap(new HashMap());<br> | ||
Set s = m.keySet(); // set of keys in hashmap<br> | Set s = m.keySet(); // set of keys in hashmap<br> | ||
synchronized(m) { // synchronizing on map | synchronized(m) { // synchronizing on map | ||
Iterator i = s.iterator(); // Must be in synchronized block | |||
while (i.hasNext()) | |||
foo(i.next()); | |||
} | } | ||
</ | </pre> | ||
| Line 394: | Line 418: | ||
The key issue in a hash table in a parallel environment is to make sure any update/insert/delete sequences have been completed properly prior to attempting subsequent operations to make sure the data has been synched appropriately. However, since access speed is such a critical component of the design of a hash table, it is essential to try and avoid using too many locks for performing synchronization. Fortunately, a number of lock-free hash designs have been implemented to avoid this bottleneck. | The key issue in a hash table in a parallel environment is to make sure any update/insert/delete sequences have been completed properly prior to attempting subsequent operations to make sure the data has been synched appropriately. However, since access speed is such a critical component of the design of a hash table, it is essential to try and avoid using too many locks for performing synchronization. Fortunately, a number of lock-free hash designs have been implemented to avoid this bottleneck. | ||
One such example in Java is the ConcurrentHashMap | One such example in Java is the ConcurrentHashMap<ref>http://www.javamex.com/tutorials/synchronization_concurrency_8_hashmap.shtml</ref>, which acts as a synchronized version of the [http://docs.oracle.com/javase/6/docs/api/java/util/HashMap.html HashMap]. With this structure, there is full concurrency of retrievals and adjustable expected concurrency for updates. There is, however, no locking in this data structure and retrievals will typically run in parallel along with updates/deletes. Retrievals, however, will receive all most recently completed transactions even if it cannot get the values that haven't finished being updated. This both allows for efficiency and greater concurrency. | ||
'''Parallel Counter Increment Alternative:''' | '''Parallel Counter Increment Alternative:''' | ||
< | <pre> | ||
private ConcurrentMap<String,Integer> queryCounts = new ConcurrentHashMap<String,Integer>(1000);<br> | private ConcurrentMap<String,Integer> queryCounts = new ConcurrentHashMap<String,Integer>(1000);<br> | ||
private void incrementCount(String q) { | private void incrementCount(String q) { | ||
Integer oldVal, newVal; | |||
do { | |||
oldVal = queryCounts.get(q); | |||
newVal = (oldVal == null) ? 1 : (oldVal + 1); | |||
} while (!queryCounts.replace(q, oldVal, newVal)); | |||
} | } | ||
</ | </pre> | ||
The above code snippet represents an alternative to the serial option presented in the previous section, while also avoiding much of the locking that takes place using the synchronized functions or synchronized blocks. With ConcurrentHashMap, however, notice that we must implement some new code in order to handle the fact that a variety of inserts/updates could be running at the same time. The replace() function here acts much like a compare-and-set operation typically used with concurrent code. Basically, the value would be changed only if not equal to the previously mapped value. This is much more efficient that locking the entire function as we often do not expect unequal values. | The above code snippet represents an alternative to the serial option presented in the previous section, while also avoiding much of the locking that takes place using the synchronized functions or synchronized blocks. With ConcurrentHashMap, however, notice that we must implement some new code in order to handle the fact that a variety of inserts/updates could be running at the same time. The replace() function here acts much like a compare-and-set operation typically used with concurrent code. Basically, the value would be changed only if not equal to the previously mapped value. This is much more efficient that locking the entire function as we often do not expect unequal values. | ||
| Line 413: | Line 437: | ||
'''Parallel Traversal Alternative:''' | '''Parallel Traversal Alternative:''' | ||
< | <pre> | ||
Map m = new ConcurrentHashMap(); | |||
Set s = m.keySet(); // set of keys in hashmap | |||
Iterator i = s.iterator(); // Must be in synchronized block | |||
while (i.hasNext()) | |||
foo(i.next()); | |||
</ | </pre> | ||
In the case of a traversal, recall that ConcurrentHashMaps require to locking on read operations. Thus we can actually remove the synchronized condition here and iterate in a normal fashion. | In the case of a traversal, recall that ConcurrentHashMaps require to locking on read operations. Thus we can actually remove the synchronized condition here and iterate in a normal fashion. | ||
| Line 427: | Line 451: | ||
=== Introduction to Graph Data Structure === | === Introduction to Graph Data Structure === | ||
A graph data structure | A graph data structure<ref>http://en.wikipedia.org/wiki/Graph_%28abstract_data_type%29</ref> is another type of linked-list structure that focuses on data relationships and the most efficient ways to traverse from one node to another. For example, in a networking application, one network node may have connections to a variety of other network nodes. These nodes then also link to a variety of other nodes in the network. Using this connection of nodes, it would be possible to then find a path from one specific node to another in the chain. This could be accomplished by having each node contain a linked list of pointers to all other reachable nodes. | ||
[[File:250px-6n-graf.svg.png]] | [[File:250px-6n-graf.svg.png]] | ||
| Line 433: | Line 457: | ||
=== Opportunities for Parallelization === | === Opportunities for Parallelization === | ||
Graphs | Graphs<ref>http://en.wikipedia.org/wiki/Graph_%28abstract_data_type%29</ref> consist of a finite set of ordered pairs called edges or arcs, of certain entities called nodes or vertices. From one given vertex, one would typically want to order the different paths from one vertex to another using its list of edges or, more than likely, would be interested in the fastest means of getting from one of these vertexes to some sort of destination vertex. | ||
Graph nodes typically will keep their list of edges in a linked list. Also, when attempting to create a shortest path algorithm on the fly, the graph will typically use a combination of a linked list to represent the path as it's being built, along with a queue that is used for each step of that process. Synchronizing all of these can be a major challenge. | Graph nodes typically will keep their list of edges in a linked list. Also, when attempting to create a shortest path algorithm on the fly, the graph will typically use a combination of a linked list to represent the path as it's being built, along with a queue that is used for each step of that process. Synchronizing all of these can be a major challenge. | ||
| Line 439: | Line 463: | ||
Much like the hash table, graphs cannot afford to be slow and must often generate results in a very efficient manner. Having to lock on each list of edges or locking on a shortest path list would really be a major obstacle. | Much like the hash table, graphs cannot afford to be slow and must often generate results in a very efficient manner. Having to lock on each list of edges or locking on a shortest path list would really be a major obstacle. | ||
Certainly though, the need for parallel processing becomes critical when you consider, for example, that social networking has become such a major proponent of graph algorithms. Facebook now has roughly a billion users | Certainly though, the need for parallel processing becomes critical when you consider, for example, that social networking has become such a major proponent of graph algorithms. Facebook now has roughly a billion users<ref>http://www.facebook.com/press/info.php?statistics</ref> and each user has series of friend links that must be analyzed and examined. This list just keeps growing and growing. | ||
One of the most significant opportunities for a parallel algorithm with a graph data structure is with the traversal algorithms. We can use Breadth-First search | One of the most significant opportunities for a parallel algorithm with a graph data structure is with the traversal algorithms. We can use Breadth-First search<ref>http://en.wikipedia.org/wiki/Breadth-first_search</ref> as an example of this, starting from an initial node and expanding outwards until reaching the destination node. | ||
=== Serial Code Examples === | === Serial Code Examples === | ||
| Line 449: | Line 473: | ||
The following shows a sample of a bread first algorithm which traverses from the city of Frankfurt to Augsburg and Stuttgart Germany. In does so, the graph begins at a root node (Frankfurt) and expands outwardly to all connected nodes on each step. From there, each of those nodes proceeds to expand the search outwards until all nodes have been covered. | The following shows a sample of a bread first algorithm which traverses from the city of Frankfurt to Augsburg and Stuttgart Germany. In does so, the graph begins at a root node (Frankfurt) and expands outwardly to all connected nodes on each step. From there, each of those nodes proceeds to expand the search outwards until all nodes have been covered. | ||
[[File:GermanyBFS.png]] | [[File:GermanyBFS.png]]<ref>http://en.wikipedia.org/w/index.php?title=File%3AGermanyBFS.svg</ref> | ||
The following code snippet implements a BFS search function. This function utilized coloring schemes and marks to denote that a node has been visited. It begins with an initial vertex in a queue and expands outward to all its successors until no further elements remain unmarked. | The following code snippet implements a BFS search function. This function utilized coloring schemes and marks to denote that a node has been visited. It begins with an initial vertex in a queue and expands outward to all its successors until no further elements remain unmarked.<ref>http://renaud.waldura.com/portfolio/graph-algorithms/classes/graph/BFSearch.java</ref> | ||
< | <pre> | ||
public void search(Graph g) | public void search(Graph g) | ||
{ | { | ||
g.paint(Color.white); // paint all the graph vertices with white | |||
g.mark(false); // unmark the whole graph | |||
refresh(null); // and redraw it | |||
Vertex r = g.root(); // the root is painted grey | |||
g.paint(r, Color.gray); refresh(g.box(r)); | |||
java.util.Vector queue = new java.util.Vector(); | |||
queue.addElement(r); // and put in a queue | |||
while(!queue.isEmpty()) | |||
{ | |||
Vertex u = (Vertex) queue.firstElement(); | |||
queue.removeElement(u); // extract a vertex from the queue | |||
g.mark(u, true); refresh(g.box(u)); | |||
int dp = g.degreePlus(u); | |||
for(int i = 0; i < dp; i++) // look at its successors | |||
{ | |||
Vertex v = g.ithSucc(i, u); | |||
if(Color.white == g.color(v)) | |||
{ | |||
queue.addElement(v); | |||
g.paint(v, Color.gray); refresh(g.box(v)); | |||
} | |||
} | |||
g.paint(u, Color.black); refresh(g.box(u)); | |||
g.mark(u, false); refresh(g.box(u)); | |||
} | |||
} | } | ||
</ | </pre> | ||
=== Parallel Solution === | === Parallel Solution === | ||
| Line 493: | Line 517: | ||
< | <pre> | ||
for all vertices u at level d in parallel do | |||
for all adjacencies v of u in parallel do | |||
dv = D[v]; | |||
if(dv < 0) // v is visited for the first time | |||
vis = fetch_and_add(&Visited[v], 1); '''LOCK''' | |||
if(vis == 0) // v is added to a stack only once | |||
D[v] = d+1; | |||
pS[count++] = v; // Add v to local thread stack | |||
fetch_and_add(&sigma[v], sigma[u]); '''LOCK''' | |||
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v '''LOCK''' | |||
if(dv == d + 1) | |||
fetch_and_add(&sigma[v], sigma[u]); '''LOCK''' | |||
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v '''LOCK''' | |||
</ | </pre> | ||
A much better parallel algorithm is represented in the following pseudocode. Notice that each of the vertices is sent to a separate processor and send/receive operations will eventually sync up the path information. | A much better parallel algorithm is represented in the following pseudocode. Notice that each of the vertices is sent to a separate processor and send/receive operations will eventually sync up the path information. | ||
[[File:Parallel-code.PNG]] | [[File:Parallel-code.PNG]]<ref>http://sc05.supercomputing.org/schedule/pdf/pap346.pdf</ref> | ||
The following graph also shows how now each of the regional sets of vertices being search can be added to the path in a parallel fashion. | The following graph also shows how now each of the regional sets of vertices being search can be added to the path in a parallel fashion. | ||
[[File:Parallel-graph.PNG]] | [[File:Parallel-graph.PNG]]<ref>http://www.cc.gatech.edu/~bader/papers/PPoPP12/PPoPP-2012-part2.pdf</ref> | ||
Every set of vertices in the same distance from the source is assigned to a processor. This set of vertices is called a regional set of vertices. The goal is to find the shortest path connecting each region. | Every set of vertices in the same distance from the source is assigned to a processor. This set of vertices is called a regional set of vertices. The goal is to find the shortest path connecting each region. | ||
| Line 547: | Line 571: | ||
10. Describe a parallel alternative in a graph data structure. | 10. Describe a parallel alternative in a graph data structure. | ||
= References = | ='''References'''= | ||
<div id="referencesAnchor"></div> | |||
<references /> | |||
Latest revision as of 00:33, 18 March 2015
Chapter 5a CSC/ECE 506 Spring 2015 / Other linked data structures
Original wiki : http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2014/5a_rm
Topic Write-up: http://courses.ncsu.edu/csc506/lec/001/homework/ch5_6.html
Overview
Linked Data Structures (LDS) consists of different types of data structures such as linked lists, trees, hash tables and graphs. Although each structure is diversed, LDS traversal shares a common characteristic in reading a node and discovering the other nodes it points to. Hence, this often introduces loop carried dependence. Chapter 5 of Solihin, discusses various algorithms on parallelizing LDS using a simple linked list. In this wiki, we attempt to cover other LDS such as trees, hashes and graphs, and see how the parallelization algorithms discussed can be applied to these structures.
Introduction to Linked-List Parallel Programming
A linked list is a data structure which contains a set of nodes. Nodes in linked list are composed of data and references to next node. It is the simplest form of linked data structures. Other linked data structures include Trees, Hash Tables and Graphs. One component that tends to link together various linked data structures is their dependence at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket in order to resolve collisions, trees have linked lists with left and right tree node paths, and graphs have linked lists to determine the paths.
To understand how parallelization techniques are applied to linked data structures, a copy-scan technique is illustrated in brief, which is further extended to a partial sum computation in a linked list.
For an array processing algorithm, a common technique used at the processor level is the copy-scan technique. This technique involves copying rows of data from one processor to another in a log(n) fashion until all processors have their own copy of that row. From there, you could perform a reduction technique to generate a sum of all the data, all while working in a parallel fashion. Take the following grid:<ref>http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html</ref>
The basic process for copy-scan would be to:
- In the first step, copy the row 1 elements to corresponding index numbers of row 2 array.
- In second step, copy the row 1 elements to corresponding indexes in array of row 3, similarly row 2 elements -> row 4.
- In this manner, in the nth step, 2^n rows can copied to 2^n rows
- This can operation is performed until all rows have been copied in a log(n) fashion.
- Perform the parallel operations to generate the desired result (reduction for sum, etc.).
With linked lists, there is a concept called pointer doubling, which works in a very similar manner to copy-scan.<ref>http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html</ref>
- Each processor will make a copy of the pointer it holds to its neighbor.
- Next, each processor will make a pointer to the processor 2 steps away.
- This continues in logarithmic fashion until each processor has a pointer to the end of the chain.
- Perform the parallel operations to generate the desired result.
Pointer doubling or pointer jumping can be used for performing partial sums of a linked list. This is accomplished by adding the value held by the node with the value stored in the node it is pointing to. This is repeated until all pointers have reached the end of the list. The result is a linked list which contains the sum of the node and all preceding nodes. Below is an example of this algorithm in action.
The advantages of pointer jumping<ref>http://en.wikipedia.org/wiki/Pointer_jumping</ref> aren't just for single linked lists. This algorithm can also be used to find the root of a tree (this will be discussed in detail in the later section). The way in which this algorithm is used, is similar to the previous example. Each node will point to the next node until it reaches the end. The result is that every node will have a pointer to the root of the tree. Below diagram shows an example which illustrates the algorithm discussed.<ref>Calvin C.-Y.Chen, Sajal K. Das, "Parallel Breadth-first and Breadth-depth traversals of general trees", Advances in Computing and Information - ICCP '90, ISBN: 978-3-540-46677-2</ref>

However, with linked list programming, similar to array-based programming, it becomes imperative to have some sought of locking mechanism or other parallel technique for critical sections in order to avoid race conditions. To make sure the results are correct, it is important that operations can be serialized appropriately and that data remains current and synchronized.
In this chapter, we will explore parallelization opportunities for hash tables, trees, and graph linked data structures.
Trees
Introduction to Trees
A tree data structure <ref>http://en.wikipedia.org/wiki/Tree_%28data_structure</ref> contains a set of ordered nodes with one parent node followed by zero or more child nodes. Typically this tree structure is used with searching or sorting algorithms to achieve log(n) efficiencies. Assuming you have a balanced tree, or a relatively equal set of nodes under each branching structure of the tree, and assuming a proper ordering structure, searches/inserts/deletes should occur far more quickly than having to traverse an entire list.
Opportunities for Parallelization
One potential slowdown in a tree data structure could occur during the traversal process. Even though search/update/insert can occur in a logarithmic fashion, traversal operations such as in-order, pre-order, post-order traversals can still require a full sequence of the list to generate all output. This gives an opportunity to generate parallel code by having various portions of the traversal occur on different processors.
Serial Code Example
In this section, we will begin by showing different serial tree traversal algorithms<ref>http://en.wikipedia.org/wiki/Tree_traversal</ref> using the tree shown below.
1
/ \
/ \
/ \
2 3
/ \ /
4 5 6
/ / \
7 8 9
The correct output should look like this: preorder: 1 2 4 7 5 3 6 8 9 inorder: 7 4 2 5 1 8 6 9 3 postorder: 7 4 5 2 8 9 6 3 1 level-order: 1 2 3 4 5 6 7 8 9 |
Tree Traversal
|
Procedure Tree_Traversal is type Node;
type Node_Access is access Node;
type Node is record
Left : Node_Access := null;
Right : Node_Access := null;
Data : Integer;
end record;
|
Tree Destroy
|
Procedure Destroy_Tree(N : in out Node_Access) is procedure free is new Ada.Unchecked_Deallocation(Node, Node_Access);
begin
if N.Left /= null then
Destroy_Tree(N.Left);
end if;
if N.Right /= null then
Destroy_Tree(N.Right);
end if;
Free(N);
end Destroy_Tree;
|
Node Access
|
Function Tree(Value : Integer; Left : Node_Access; Right : Node_Access) return Node_Access is Temp : Node_Access := new Node; begin Temp.Data := Value; Temp.Left := Left; Temp.Right := Right; return Temp; end Tree; |
Preorder
|
Procedure Preorder(N : Node_Access) is begin
Put(Integer'Image(N.Data));
if N.Left /= null then
Preorder(N.Left);
end if;
if N.Right /= null then
Preorder(N.Right);
end if;
end Preorder;
|
Inorder
|
Procedure Inorder(N : Node_Access) is begin
if N.Left /= null then
Inorder(N.Left);
end if;
Put(Integer'Image(N.Data));
if N.Right /= null then
Inorder(N.Right);
end if;
end Inorder;
|
Postorder
|
Procedure Postorder(N : Node_Access) is begin
if N.Left /= null then
Postorder(N.Left);
end if;
if N.Right /= null then
Postorder(N.Right);
end if;
Put(Integer'Image(N.Data));
end Postorder;
|
Levelorder
|
Procedure Levelorder(N : Node_Access) is Package Queues is new Ada.Containers.Doubly_Linked_Lists(Node_Access);
use Queues;
Node_Queue : List;
Next : Node_Access;
begin
Node_Queue.Append(N);
while not Is_Empty(Node_Queue) loop
Next := First_Element(Node_Queue);
Delete_First(Node_Queue);
Put(Integer'Image(Next.Data));
if Next.Left /= null then
Node_Queue.Append(Next.Left);
end if;
if Next.Right /= null then
Node_Queue.Append(Next.Right);
end if;
end loop;
end Levelorder;
|
main
N : Node_Access;
begin
N := Tree(1,
Tree(2,
Tree(4,
Tree(7, null, null),
null),
Tree(5, null, null)),
Tree(3,
Tree(6,
Tree(8, null, null),
Tree(9, null, null)),
null));
Put("preorder: ");
Preorder(N);
New_Line;
Put("inorder: ");
Inorder(N);
New_Line;
Put("postorder: ");
Postorder(N);
New_Line;
Put("level order: ");
Levelorder(N);
New_Line;
Destroy_Tree(N);
end Tree_traversal;
|
Parallel Solution
Now that we have seen standard tree traversal techniques, we will look at how tree traversal can be parallelized. Tree is a good candidate to exploit parallelism. Since each node/sub-tree is independent in a binary tree, a large tree can be split up into 2, 4, 8, or more subtrees and each processor holds a sub-tree. In this method, the only data that is common to all processors are the parent nodes of all sub-trees. Consider a perfect balanced binary tree which has k levels. So the total number of nodes in the tree will be equal to 2^k-1. An example of perfect balanced binary tree is shown in the figure below. For the example shown below, four processors are required if each sub-tree labelled Rank 0, Rank 1, Rank 2 and Rank 3 is assigned to a single processor. The three nodes colored in red is the common data shared by all processors.So in this scenario, four processors each have four independent sub-trees and they share three nodes. In general, if n processors each have n independent sub-trees, they share n-1 nodes in common. If the size of the tree was increased and the number of processors was also increased, the number of shared nodes would also increase to support the increased number of sub-trees.<ref>http://www.shodor.org/media/content//petascale/materials/UPModules/Binary_Tree_Traversal/Binary_Tree_Traversal_Module_Document.pdf</ref>
The fact that trees are comprised of independent sub-trees makes parallelizing them very easy. Properly done, the portion of these traversals that is parallelizable grows at 2n for an n-generation tree. While the processors only need to synchronize once, at the end, the parallelizable portion approaches 100% for large trees (but keep in mind Amdahl’s Law, footnote 1). The basic steps for parallelizing these traversals are as follows:
- Perform the traversal on the parent part of the tree.
- Whenever you get to a node that is only present on one processor, ask that processor to execute the appropriate C algorithm detailed above.
- The processor will return its result that can be used exactly as if it was a serial processor.
A Breadth-First traversal is somewhat more complicated to implement as a parallel system because at each level, it must access nodes from all of the parallel processors. Theoretically, a Breadth-First traversal can achieve complete parallelization of Pre-, In-, and Post-Order traversals. As the degree of parallelism is increased, the speed up increases as per Amdahl's law. One thing to remember in the parllelization though, is that the amount of processor-to-processor data transmission adds in a greater potential for delays, thus slowing down the algorithm. Nevertheless, as the size of the tree increases the size of the generations grows at the rate of 2n while the number of synchronizations grows at a rate of n for an n-generation tree, so the parallelizable portion of these traversals also approaches 100%. The basic steps for parallelizing this traversal are as follows:
- Perform the traversal on the parent part of the tree.
- Whenever you get to a node that is only present on one processor, ask that processor to execute the Breadth-First C algorithm detailed above, but wait after it finishes one generation.
- Combine all the one-generation results from the different processors in the correct order.
- Allow each processor to execute the next generation of the Breadth-First C algorithm detailed above, and then wait again.
- Repeat Steps 3 and 4 until there are no nodes remaining
Here, since each processor is assigned an independent sub-tree, elaborate locks are not required.
An example of a parallel Breadth-First tree traversal is shown below.
The data structure can be constructed from the input tree using the GEN-COMP-NEXT algorithm. The result is a linked list from the input tree which is represented as a "parent-of" relation with explicit ordering of children.
Algorithm GEN-COMP-NEXT:
for all Pi, 1<=i<=n, do
parallel begin
Step 1: Processor Pi builds the jth field of i's parent node if i is the jth child of its parent. The jth field (if it is not the last field) is stored in the ith index of array SUPERNODE.
Step 2: Processor Pi builds node i's last fiend whose array index is (n+1)
parallel end
Below is the algorithm to perform a Breadth-First tree traversal in parallel where bfrank is the output parameter, array[1..n] of integer; level is the input parameter, array[1..n] of integer; and preorder list is an input parameter, array[1..n] of integer.
Algorithm BF-TRAVERSAL (bfank, level, preorder-list)
Step 1. Divide the preorder-list into p blocks. Each processor builds partial lists from the nodes in the block. The header and the taller arrays for the lists built by processor i are denoted by hd[*,i] and tl[*,i], respectively.
for all Pi, 1<=i<=p do
parbegin
Pi works on nodes pre-order-list[k], where (i-1)*(n/p) <= k < (i*n/p)
Pi initializes list[k] to zreo /* the successor of k-th input in a partial list */
/* Phase 1. Pi initializes entries in hd[*,i] and tl[*,i] that are used and entries in hdflag */
hd[level[preorder-list[k]], i] := 0; tl[level[preorder-list[k]], i] := 0; hdflag[k] := 0;
/* Phase 2. Build partial lists */
Pi adds each of the n/p nodes to the partial list for the level of that node and updates hd[*,i], tl[*, i], and list [*] accordingly.
parend;
Step 2. Link up partial lists.
/* Phase 1. Initialize header and tailer for the global lists */
for all Pi, 1 <= i <= p, do
initialize head[k] and tail[k] to zero, for (i-1)*n/p <= k < (i*n/p)
P1 sets head[n+1] and tail[n+1] to zero;
/* Phase 2. Link partial lists to form a list for each level */
for each of the p blocks do
for all Pi, 1 <= i <= p, do /* all processors work on the same block */
parbegin
for i := 1 to (n/p^2) do
begin
Pi is given at most a node mi in each iteration.
if hdflag[mi] = 1 /* The first element in its partial list */
then
if the global list for the level of node mi is empty
then
let head[level[mi]] and tail[level[mi]] point to mi
else
list[tail[level[mi]]] := mi and update tail[level[mi]] to be the tail of the partial list for mi.
end;
parend;
Step 3. Create a linked list to implement the NEXT function
for all Pi, 1 <= i <= p, do
parbegin
for k := (i-1)*(n/p)+1 to (i*n/p) do
if(head[k] != 0 and head[k+1] != 0) then list[tail[k]] := head[k+1];
parend;
Step 4. Obtain ranking
LINKED-LIST-RANKING(list, tmp-rank, n);
Step 5. Output the result
for all Pi, 1 <= i <= p, do
parbegin
for k := (i-1)*(n/p)+1 to (i*n/p) do bfrank[preorder-list[k]] := tmp-rank[k];
parend;
To obtain the required tree-traversals, the following rules are operated on the linked list produced by algorithm GEN-COMP-NEXT:
- pre-order traversal: select the first copy of each node;
- post-order traversal: select the last copy of each node;
- in-order traversal: delete the first copy of each node if it is not a leaf and delete the last copy of each node if it has more than one child.
Since the tree is transformed into a linked list by the GEN-COMP-NEXT function, it can be locked while editing as per the LDS chapter in Solihin book. Either a Global lock approach, Fine Grained approach or Read-Write Locks can be used. Since the tree is able to be transformed into a simple linked list, we are able to use the same locking mechanism for multiple linked data structure types. In this fashion we have broken up the linked list of the tree into successive parts and imposed a divide-and-conquer technique to complete the traversal.
Hash Tables
Introduction to Hash Tables
Hash tables<ref>http://www.devjavasoft.org/code/classhashtable.html</ref> are very efficient data structures often used in searching algorithms for fast lookup operations. They are used extensively in data processing as in involves a vast amount of data through the hash table using as few indirection's in the storage structure as possible.
A single hash table level look can easily become a bottleneck, thus several method were developed to overcome this difficulty. Hash tables contain a series of "buckets" that function like indexes into an array, each of which can be accessed directly using their key value. The bucket for which a piece of data will be placed is determine by a special hashing function.
The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value.
In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list. <ref>http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg</ref>
There are several parallel implementations of hash tables available that use lock-based synchronization. Larson et al. use two lock levels, there is one global table level lock, and there is one separate lightweight lock (a flag) for each bucket. The high level lock is just used for setting the bucket level flags and released right afterwards. This ensures a fine grained mutual exclusion (concurrent operations on bucket level), but needs only one real lock for the implementation.
A scalable hash table for shared memory multi-processor (SMP) supports very high rates of concurrent operations (e.g., insert, delete, and lookup), while simultaneously reducing cache misses. The SMP system has a memory subsystem and a processor subsystem interconnected via a bus structure.
The hash table is stored in the memory subsystem to facilitate access to data items. The hash table is segmented into multiple buckets, with each bucket containing a reference to a linked list of bucket nodes that hold references to data items with keys that hash to a common value. Individual bucket nodes contain multiple signature-pointer pairs that reference corresponding data items. Each signature-pointer pair has a hash signature computed from a key of the data item and a pointer to the data item. The first bucket node in the linked list for each of the buckets is stored in the hash table.
To enable multithread access, while serializing operation of the table, the SMP system utilizes two levels of locks: a table lock and multiple bucket locks. The table lock allows access by a single processing thread to the table while blocking access for other processing threads. The table lock is held just long enough for the thread to acquire the bucket lock of a particular bucket node. Once the table lock is released, another thread can access the hash table and any one of the other buckets.
Opportunities for Parallelization
Hash tables can be very well suited to parallel applications. For example, system code responsible for caching between multiple processors could itself be an ideal opportunity for a shared hashmap. Each processor sharing one common cache would be able to access the relevant information all in one location.
This would, however, involve a good bit of synchronization, as each processor would need to wait in case a lock was being placed on a specific bucket in the cache hashmap. Unfortunately, traditional locking would be a bad solution to this problem as processors need to run very quickly. Having to wait for locks would destroy the application processing time. The need for a non-locking solution is critical to performance.
In Java, the standard class utilized for hashing is the HashMap<ref>http://code.wikia.com/wiki/Hashmap</ref> class. This class has a fundamental weakness though in that the entire map requires synchronization prior to each access. This causes a lot of contention and many bottlenecks on a parallel machine.
Below, I will present a Java-based solution to this problem by using a ConcurrentHashMap class. This class only requires a portion of the map to be locked and reads can generally occur with no locking whatsoever.
Serial Code Examples
Simple synchronized example to increment a counter.<ref>http://www.javamex.com/tutorials/synchronization_concurrency_8_hashmap.shtml</ref>
private Map<String,Integer> queryCounts = new HashMap<String,Integer>(1000);<br>
private '''synchronized''' void incrementCount(String q) {
Integer cnt = queryCounts.get(q);
if (cnt == null) {
queryCounts.put(q, 1);
} else {
queryCounts.put(q, cnt + 1);
}
}
The above code was written using an ordinary HashMap data structure. Notice that we use the synchronized keyword here to signify that only one thread can enter this function at any one point in time. With a really large number of threads, however, waiting to enter the synchronized operation could be a major bottleneck.
Iterator example for synchronized HashMap.
Map m = Collections.synchronizedMap(new HashMap());<br>
Set s = m.keySet(); // set of keys in hashmap<br>
synchronized(m) { // synchronizing on map
Iterator i = s.iterator(); // Must be in synchronized block
while (i.hasNext())
foo(i.next());
}
In the above example, we show how an iterator could be used to traverse over a map. In this case, we would need to utilize the synchronizedMap function available in the Collections interface. Also, as you may notice, once the iterator code begins we must actually synchronize on the entire map in order to iterate through the results. But what if several processors wish to iterate through at the same time?
Parallel Solution
The key issue in a hash table in a parallel environment is to make sure any update/insert/delete sequences have been completed properly prior to attempting subsequent operations to make sure the data has been synched appropriately. However, since access speed is such a critical component of the design of a hash table, it is essential to try and avoid using too many locks for performing synchronization. Fortunately, a number of lock-free hash designs have been implemented to avoid this bottleneck.
One such example in Java is the ConcurrentHashMap<ref>http://www.javamex.com/tutorials/synchronization_concurrency_8_hashmap.shtml</ref>, which acts as a synchronized version of the HashMap. With this structure, there is full concurrency of retrievals and adjustable expected concurrency for updates. There is, however, no locking in this data structure and retrievals will typically run in parallel along with updates/deletes. Retrievals, however, will receive all most recently completed transactions even if it cannot get the values that haven't finished being updated. This both allows for efficiency and greater concurrency.
Parallel Counter Increment Alternative:
private ConcurrentMap<String,Integer> queryCounts = new ConcurrentHashMap<String,Integer>(1000);<br>
private void incrementCount(String q) {
Integer oldVal, newVal;
do {
oldVal = queryCounts.get(q);
newVal = (oldVal == null) ? 1 : (oldVal + 1);
} while (!queryCounts.replace(q, oldVal, newVal));
}
The above code snippet represents an alternative to the serial option presented in the previous section, while also avoiding much of the locking that takes place using the synchronized functions or synchronized blocks. With ConcurrentHashMap, however, notice that we must implement some new code in order to handle the fact that a variety of inserts/updates could be running at the same time. The replace() function here acts much like a compare-and-set operation typically used with concurrent code. Basically, the value would be changed only if not equal to the previously mapped value. This is much more efficient that locking the entire function as we often do not expect unequal values.
Parallel Traversal Alternative:
Map m = new ConcurrentHashMap();
Set s = m.keySet(); // set of keys in hashmap
Iterator i = s.iterator(); // Must be in synchronized block
while (i.hasNext())
foo(i.next());
In the case of a traversal, recall that ConcurrentHashMaps require to locking on read operations. Thus we can actually remove the synchronized condition here and iterate in a normal fashion.
Graphs
Introduction to Graph Data Structure
A graph data structure<ref>http://en.wikipedia.org/wiki/Graph_%28abstract_data_type%29</ref> is another type of linked-list structure that focuses on data relationships and the most efficient ways to traverse from one node to another. For example, in a networking application, one network node may have connections to a variety of other network nodes. These nodes then also link to a variety of other nodes in the network. Using this connection of nodes, it would be possible to then find a path from one specific node to another in the chain. This could be accomplished by having each node contain a linked list of pointers to all other reachable nodes.
Opportunities for Parallelization
Graphs<ref>http://en.wikipedia.org/wiki/Graph_%28abstract_data_type%29</ref> consist of a finite set of ordered pairs called edges or arcs, of certain entities called nodes or vertices. From one given vertex, one would typically want to order the different paths from one vertex to another using its list of edges or, more than likely, would be interested in the fastest means of getting from one of these vertexes to some sort of destination vertex.
Graph nodes typically will keep their list of edges in a linked list. Also, when attempting to create a shortest path algorithm on the fly, the graph will typically use a combination of a linked list to represent the path as it's being built, along with a queue that is used for each step of that process. Synchronizing all of these can be a major challenge.
Much like the hash table, graphs cannot afford to be slow and must often generate results in a very efficient manner. Having to lock on each list of edges or locking on a shortest path list would really be a major obstacle.
Certainly though, the need for parallel processing becomes critical when you consider, for example, that social networking has become such a major proponent of graph algorithms. Facebook now has roughly a billion users<ref>http://www.facebook.com/press/info.php?statistics</ref> and each user has series of friend links that must be analyzed and examined. This list just keeps growing and growing.
One of the most significant opportunities for a parallel algorithm with a graph data structure is with the traversal algorithms. We can use Breadth-First search<ref>http://en.wikipedia.org/wiki/Breadth-first_search</ref> as an example of this, starting from an initial node and expanding outwards until reaching the destination node.
Serial Code Examples
Bread First Search
The following shows a sample of a bread first algorithm which traverses from the city of Frankfurt to Augsburg and Stuttgart Germany. In does so, the graph begins at a root node (Frankfurt) and expands outwardly to all connected nodes on each step. From there, each of those nodes proceeds to expand the search outwards until all nodes have been covered.
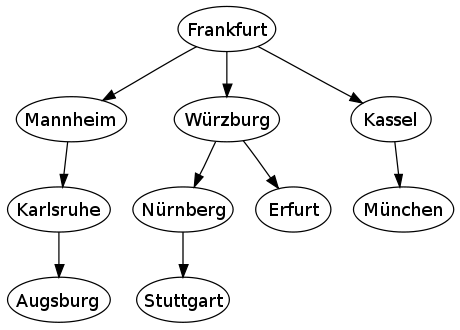 <ref>http://en.wikipedia.org/w/index.php?title=File%3AGermanyBFS.svg</ref>
<ref>http://en.wikipedia.org/w/index.php?title=File%3AGermanyBFS.svg</ref>
The following code snippet implements a BFS search function. This function utilized coloring schemes and marks to denote that a node has been visited. It begins with an initial vertex in a queue and expands outward to all its successors until no further elements remain unmarked.<ref>http://renaud.waldura.com/portfolio/graph-algorithms/classes/graph/BFSearch.java</ref>
public void search(Graph g)
{
g.paint(Color.white); // paint all the graph vertices with white
g.mark(false); // unmark the whole graph
refresh(null); // and redraw it
Vertex r = g.root(); // the root is painted grey
g.paint(r, Color.gray); refresh(g.box(r));
java.util.Vector queue = new java.util.Vector();
queue.addElement(r); // and put in a queue
while(!queue.isEmpty())
{
Vertex u = (Vertex) queue.firstElement();
queue.removeElement(u); // extract a vertex from the queue
g.mark(u, true); refresh(g.box(u));
int dp = g.degreePlus(u);
for(int i = 0; i < dp; i++) // look at its successors
{
Vertex v = g.ithSucc(i, u);
if(Color.white == g.color(v))
{
queue.addElement(v);
g.paint(v, Color.gray); refresh(g.box(v));
}
}
g.paint(u, Color.black); refresh(g.box(u));
g.mark(u, false); refresh(g.box(u));
}
}
Parallel Solution
But could we introduce parallel mechanisms into this Breadth First search? The most logical and effective way, instead of utilizing locks and synchronized regions, is to use data parallel techniques during the traversal. This can be accomplished by having each node of a given breadth search step be sent to a separate processor. So, using the above example, instead of having Frankfurt->Mannheim followed by Frankfurt->Wurzburg followed by Frankfurt->Bassel on the same processor, Frankfurt could split out all 3 searches in a parallel fashion onto 3 different processors. Then, possible some cleanup code would be left at the end to visit any remaining untouched nodes. In a network routing applications, being able to split up the search for each IP address code would make searched significantly faster that allowing one processor to be a bottleneck.
Using locking pseudocode, you might have an algorithm similar to this:
for all vertices u at level d in parallel do
for all adjacencies v of u in parallel do
dv = D[v];
if(dv < 0) // v is visited for the first time
vis = fetch_and_add(&Visited[v], 1); '''LOCK'''
if(vis == 0) // v is added to a stack only once
D[v] = d+1;
pS[count++] = v; // Add v to local thread stack
fetch_and_add(&sigma[v], sigma[u]); '''LOCK'''
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v '''LOCK'''
if(dv == d + 1)
fetch_and_add(&sigma[v], sigma[u]); '''LOCK'''
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v '''LOCK'''
A much better parallel algorithm is represented in the following pseudocode. Notice that each of the vertices is sent to a separate processor and send/receive operations will eventually sync up the path information.

The following graph also shows how now each of the regional sets of vertices being search can be added to the path in a parallel fashion.
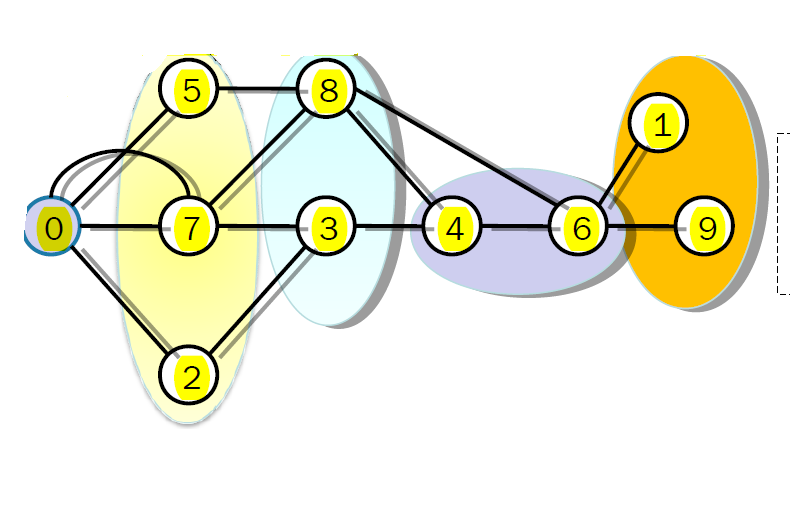
Every set of vertices in the same distance from the source is assigned to a processor. This set of vertices is called a regional set of vertices. The goal is to find the shortest path connecting each region.
As shown, maps are able to be parallelized using very similar traversal methods seen in trees. We have also highlighted the importance of graphs and their need to be accessed quickly. Due to this need for access speed, graphs benefit greatly from parallelization.
Conclusion
Through this wiki page we have shown how parallelization can be done for trees, hash tables, and graphs. While the structures are more complex than the single linked lists outlined in the Solihin textbook, their parallelization methods pull heavily from the fundamental locking techniques taught there. In several cases, the exact same locking techniques are used and it is the LDS which is manipulated to create single linked lists. In this way we are able to show how these basic principals taught by the text book are able to be expanded and carried into more complex structures and problems.
Quiz
1. Describe the copy-scan technique.
2. Describe the pointer doubling technique.
3. Which concurrency issues are of the most concern in a tree data structure?
4. What is the alternative to using a copy-scan technique in pointer-based programming?
5. Which concurrency issues are of the most concern with hash table data structures?
6. Which concurrency issues are of the most concern with graph data structures?
7. Why would you not want locking mechanisms in hash tables?
8. What is the nature of the linked list in a tree structure?
9. Describe a parallel alternative in the tree data structure.
10. Describe a parallel alternative in a graph data structure.
References
<references />