CSC/ECE 506 Spring 2014/9b vn: Difference between revisions
| (12 intermediate revisions by 2 users not shown) | |||
| Line 89: | Line 89: | ||
Performance of locking mechanisms can be improved in the following ways: | Performance of locking mechanisms can be improved in the following ways: | ||
# Optimizing software can improve the performance of locks. For instance, inserting a delay between a processor noticing a release and then trying to acquire a lock can reduce contention and bus traffic, and increase the performance of the locks. TCP-like back off algorithms can be used to adjust this delay depending on the number of threads contending for the lock.<sup><span>[[#3foot|[3]]]</span></sup> | |||
#The term "Spinning" or "Spinlock" refers to a processor waiting in a loop while trying to acquire the lock. One way to improve performance is to insert a delay between memory references so as to limit the bandwidth (traffic) each processor can use for spinning.<sup><span>[[#3foot|[3]]]</span></sup> | |||
#Additionally, fairness can be guaranteed by queuing the lock attempts in shared memory so that they happen in order.<sup><span>[[#3foot|[3]]]</span></sup> | |||
=== Avoiding Locks === | === Avoiding Locks === | ||
There are many reasons why a programmer should attempt to write programs in such a way as to avoid locks if possible | There are many reasons why a programmer should attempt to write programs in such a way as to avoid locks if possible as there are many problems that can arise with the use of locks. Some of them are discussed below<sup><span id="4body">[[#4foot|[4]]]</span></sup> | ||
One of the | One of the most well known issues is deadlock. This can occur when the threads are waiting to acquire the lock, but the lock would never be released. For example, there are two processes A and B and they need two methods (1 and 2) to be grabbed for completion of a task which are shared by both A and B. There is a potential deadlock situation when A grabs 1 and B grabs 2. Since both processes need one other method to reach completion, neither of them change their state. The solution to this problem is to set a condition where in process A can lock method 2 only if it has locked method 1. | ||
Another problem with using locks is that the performance is not optimal, | Another problem with using locks is that the performance is not optimal, since a lock is often used when there is only a chance of conflict. This approach to programming yields slower performance than what might be possible with other methods. This also leads to questions of granularity, that is how much of the code should be protected under the critical section. The programmer must decide between many small (fine grain) locks or fewer, more encompassing locks. This decision can greatly effect the performance of the program.<sup><span id="4body">[[#4foot|[4]]]</span></sup> | ||
To avoid locks, lock free programming techniques like compare and swap and sequential consistency can be followed. This pattern typically involves copying a shared variable to a local variable, performing some speculative work, and attempting to publish the changes using CAS<sup><span id="12body">[[#12foot|[12]]]</span></sup>: | To avoid locks, lock free programming techniques like compare and swap and sequential consistency can be followed. This pattern typically involves copying a shared variable to a local variable, performing some speculative work, and attempting to publish the changes using CAS<sup><span id="12body">[[#12foot|[12]]]</span></sup>: | ||
| Line 121: | Line 119: | ||
} | } | ||
} | } | ||
The above code basically follows the Read-Write-Update order and makes sure that each thread has its local copy to work on and gets it updated sequentially so that the next thread has the correct value. | The above code basically follows the Read-Write-Update order and makes sure that each thread has its local copy to work on and gets it updated sequentially so that the next thread has the correct value. In case the value is incorrect, the write fails. | ||
= Barrier Implementations = | = Barrier Implementations = | ||
In many ways, barriers are simpler than locks. A barrier is simply a point in a program where one or more threads must reach before the parallel program is allowed to continue. When using barriers, a programmer does not have to be concerned with advanced topics such as fairness, that are required when programming for locks. | In many ways, barriers are simpler than locks. A barrier is simply a point in a program where one or more threads must reach before the parallel program is allowed to continue. When using barriers, a programmer does not have to be concerned with advanced topics such as fairness, that are required when programming for locks. Some of the popular barrier techniques are listed below | ||
== Fuzzy Barrier == | |||
Barriers can have a major performance impact because of two properties. Firstly, threads that have reached a barrier are forced to wait for other barriers and as a result are in an idling state. The thread is essentially performing no useful function in this state. Secondly, the execution of the barrier itself may be slow (if implemented in software), due to the fact that they may consist of several instructions that need to execute. | |||
The fuzzy barrier aims to solve both of these issues. To increase the speed of the barrier implementation, fuzzy barriers are implemented in hardware. The other problem is to keep each thread as busy as possible for a majority of the time. This is done by extending the concept of a barrier to include a set of instructions that can be safely executed by the waiting/idling thread. By making this safe barrier region as large as possible we can ensure that almost none of the threads have to completely stall at any particular time. <sup><span id="14body">[[#14foot|[14]]]</span></sup> | |||
== Sense-Reversal Barrier == | == Sense-Reversal Barrier == | ||
This barrier is a centralized barrier where a single count variable protected by a lock is shared among all the threads. Each thread on reaching the barrier increments its value and waits till the value of variable has reached the number of threads for which barrier was implemented.Since all the threads are spinning around a single variable the miss rate | This barrier is a centralized barrier where a single count variable protected by a lock is shared among all the threads. Each thread on reaching the barrier increments its value and waits till the value of variable has reached the number of threads for which barrier was implemented. Since all the threads are spinning around a single variable the miss rate scales quadratically with number of processors. | ||
[[Image:Ch9wiki01.png]]<sup><span id="8body">[[#8foot|[8]]]</span></sup> | [[Image:Ch9wiki01.png]]<sup><span id="8body">[[#8foot|[8]]]</span></sup> | ||
| Line 217: | Line 220: | ||
== Disseminating Barrier == | == Disseminating Barrier == | ||
In this barrier each thread maintains a record of the activity of other threads. For every round i with n threads, thread A notifies thread (A + 2i) mod n. Thus after log(n) rounds all the threads are aware of the status of every other thread running and whether it has reached the barrier. Overall synchronization is achieved by implication from a carefully chosen sequence of pairwise synchronizations. | In this barrier each thread maintains a record of the activity of other threads. For every round 'i' with n threads, thread A notifies thread (A + 2i) mod n. Thus after log(n) rounds all the threads are aware of the status of every other thread running and whether it has reached the barrier. Overall synchronization is achieved by implication from a carefully chosen sequence of pairwise synchronizations. | ||
[[Image:Ch9wiki04.png]]<sup><span id="9body">[[#9foot|[9]]]</span></sup> | [[Image:Ch9wiki04.png]]<sup><span id="9body">[[#9foot|[9]]]</span></sup> | ||
| Line 232: | Line 235: | ||
} | } | ||
Here, each thread executes the same code, choosing partners for the pairwise synchronizations as a function of its own identifier and the internal | Here, each thread executes the same code, choosing partners for the pairwise synchronizations as a function of its own identifier and the internal iteration. Our own arrive flag is now set by an “in-coming” partner, who is distinct from our “out-going” partner (except when p=2). | ||
iteration.Our own arrive flag is now set by an “in-coming” partner, who is distinct from our “out-going” partner (except when p=2). | |||
== Performance Evaluation == | == Performance Evaluation == | ||
To evaluate lock performance, we can use these two criteria: | To evaluate lock performance, we can use these two criteria:<sup><span id="2body">[[#2foot|[2]]]</span></sup> | ||
=== Latency === | === Latency === | ||
Latency can be defined as the time taken to enter and exit a barrier. Ideally the latency of a barrier should be small, but for barriers that do not scale well, latency can increase as the number of threads increases.<sup><span id="1body">[[#1foot|[1]]]</span></sup> | |||
Ideally | === Traffic === | ||
Traffic is the communications overhead required by the barrier. Ideally barrier traffic should be low, as excess traffic limits scalability.<sup><span id="1body">[[#1foot|[1]]]</span></sup> | |||
== | == Performance Comparison == | ||
The comparison of the performance of some of the barrier implementations have been tabulated below: | |||
{| class="wikitable" border="1" | {| class="wikitable" border="1" | ||
|+Performance Comparison of Barrier Implementations<sup><span id="2body">[[#2foot|[2]]]</span></sup> | |+Performance Comparison of Barrier Implementations<sup><span id="2body">[[#2foot|[2]]]</span></sup> | ||
| Line 287: | Line 287: | ||
<span id="12foot">[[#12body|12.]]</span>Jeff Pershing. (2012, Jun 12). "An Introduction to Lock Free programming". Retreived from [http://preshing.com/20120612/an-introduction-to-lock-free-programming here]<br> | <span id="12foot">[[#12body|12.]]</span>Jeff Pershing. (2012, Jun 12). "An Introduction to Lock Free programming". Retreived from [http://preshing.com/20120612/an-introduction-to-lock-free-programming here]<br> | ||
<span id="13foot">[[#13body|13.]]</span>Maurice Herlihy and Nir Shavit. The Art of Multiprocessor Programming. Morgan Kauffman. March 03,1998<br> | <span id="13foot">[[#13body|13.]]</span>Maurice Herlihy and Nir Shavit. The Art of Multiprocessor Programming. Morgan Kauffman. March 03,1998<br> | ||
<span id="14foot">[[#14body|14.]]</span>Rajiv Gupta. The Fuzzy Barrier: A Mechanism for High Speed Synchronization of Processors. 1989.<br> | |||
Latest revision as of 01:01, 24 April 2014
Instruction and Previous Work
Changes are made as per the instructions given in https://docs.google.com/a/ncsu.edu/document/d/1Xk0HiD31nKXVxFt3MfNh-SLftvS4mAhlzYPBIuojAEk/edit?pli=1#
Previous Version can be found here: http://wiki.expertiza.ncsu.edu/index.php/CSC/ECE_506_Spring_2013/9b_sc
Synchronization
In addition to a proper cache coherency model, it is important for a multiprocessor system to provide support for synchronization. This must be provided at the hardware level and can also be implemented to some degree in the software. The most common types of hardware synchronization mechanisms are locks and barriers which are discussed in the further sections.
Hardware vs. Operating System Synchronization
Synchronizations are characterized by three parts: acquire, wait and release. Both hardware and operating system synchronization rely on atomic instructions for acquire and release but the implementations for the wait portion of a synchronization mechanism can vary. Hardware implementations usually use busy-waiting, where a process repeatedly tests a variable waiting for it to change. The operating system can wait using blocking, where the process suspends itself until woken up by another process.
Blocking has the advantage of freeing up the processor for use by other processes but requires operating system functions to work and consequently has a lot of overhead. Busy-waiting has much less overhead but uses the processor and cache resources while waiting. Because of these tradeoffs, it is usually better to use busy-waiting for short wait periods and blocking for long wait periods.[1]
Lock Implementations
Locks are an important concept when programming for multiprocessor systems. The purpose of a lock is to protect the code inside the lock, known as a critical section. It must be certain that while some thread X has entered the critical section, another thread Y is not also inside of the critical section and possibly modifying critical values. While thread X has entered the critical section, thread Y must wait until X has exited before entering. This can be accomplished in a variety of ways of varying complexity and performance.
Atomic Instructions
Since a multiprocessor system cannot disable interrupts as an effective method to execute code atomically, there must be hardware support for atomic operations.[4]
The ability to execute an atomic instruction is a requirement for most lock implementations. It is important that when a processor attempts to set a lock, either the lock is fully set and the thread is able to enter into the critical section, or the lock is not set and it appears that none of the instructions required to set the lock have executed.
In the x86 instruction set the opcode CMPXCHG (compare and exchange) can be used in a lock implementation in order to guarantee atomicity. This function works by sending a destination and a source. The accumulator is compared to the destination and, if they are equal, loaded with the source. If they are not equal the accumulator is loaded with the destination value. In order to assure that this is executed atomically the opcode must be issued with the LOCK prefix. This is useful in implementing some locks, such as ticket locks.[5] The syntax for the instruction is LOCK CMPXCHG SOURCE DESTINATION. Here, the source has to be a register while the destination can be either Register or Memory. An example of LOCK CMPXCHG is implementation in dis-assembly of Linux kernel's rtc_cmos_read(). The CPU locks needs to be copied and and then updated to a non zero value if the lock is to be applied. But there is a possibility when the value got copied earlier and changed later. This causes a race condition. Hence,it helps in briefing the busy wait loop by preventing race condition. The pseudo code for same is given as below[10]:
spin: # see if the lock-variable is clear mov cmos_lock, %eax test %eax, %eax jnz spin # ok, now we try to grab the lock lock cmpxchg %edx, cmos_lock # did another CPU grab it first? test %eax, %eax jnz spin
Hand-off Lock
Another type of lock that is not discussed in the text is known as the "hand-off" lock. In this lock the first thread acquires the lock if no other thread is currently locked (since it is the first thread). When another thread attempts to gain the lock it will see that the lock is in use and adds itself to the queue. Once done this thread can sleep until called by the thread with the lock. Once the thread in the lock is finished, it will pass the lock to the next thread in the queue[6]. Waiting thread gives up processor so that other threads (e.g. the thread with the lock) can run more quickly. Someone wakes up thread when the lock is free. The separation of ready queue from that of waiting queue fastens the process of execution. In the below example, the lock is given to a waiting thread by the unlock method. The interrupts are enabled only when the thread is placed in waiting queue and disabled once its given the lock.
lock () {
disable interrupts
if (value == FREE) {
value = BUSY
}
else {
add thread to queue of threads waiting for
this lock
switch to next runnable thread
}
enable interrupts
}
unlock () {
disable interrupts
value = FREE
if (any thread is waiting for this lock) {
move waiting thread from waiting queue to
ready queue
value = BUSY
}
enable interrupts
}
But this fails if interrupt happens after thread enable interrupts Lock() adds thread to wait queue Lock() enables interrupts Interrupts causes pre-emption, i.e. switch to another thread. Pre-emption moves thread to ready queue. Now thread is on two queues (wait and ready)! Also, switch is likely to be a critical section Adding thread to wait queue and switching to next thread must be atomic. Solution to this problem is waiting thread leaves interrupts disabled when it calls switch. Next thread to run has the responsibility of re-enabling interrupts before returning to user code. When waiting thread wakes up, it returns from switch with interrupts disabled (from the last thread)[11]
Performance Evaluation
Lock performance can be evaluated using the below four criteria:[2]
Acquisition Latency
Acquisition latency can be defined as the time taken to acquire the lock. This factor must be low, especially for applications that repeatedly acquire and release locks. Over the run time of a program, the acquisition latency compounded many times could have a large performance affect. However, low acquisition latency has to be balanced against other factors when implementing a lock.[1]
Traffic
Traffic can be defined as the bus traffic that is generated by the threads when attempting to acquire the lock. It is an important consideration when evaluating lock performance. If acquiring lock causes excess bus traffic, it will not scale well with the increase in the number of threads. This might lead to the eventual chocking of the bus.[1]
Fairness
In general, threads should acquire a lock in them same order that the locks were requested. With the increase in the number of threads if this condition is not enforced, some of the threads might get starved.[1]
Storage
The amount of storage needed per lock should be small enough such that it scales to a large number of threads without any problems. If a large amount of storage is required, then multiple threads could cause the locks to consume too much memory.[1]
Performance Comparison
Two common lock implementations are test&set and test-and-test&set. In terms of performance, both have a low storage cost (scalable) but are not fair. Test&set has a low acquisition latency but is not scalable due do high bus traffic when there is high contention for the lock. Test-and-test&set has a higher acquisition latency but scales better because it generates less bus traffic. The figure below shows performance comparisons for these two lock implementations.[1]

Improving performance
Performance of locking mechanisms can be improved in the following ways:
- Optimizing software can improve the performance of locks. For instance, inserting a delay between a processor noticing a release and then trying to acquire a lock can reduce contention and bus traffic, and increase the performance of the locks. TCP-like back off algorithms can be used to adjust this delay depending on the number of threads contending for the lock.[3]
- The term "Spinning" or "Spinlock" refers to a processor waiting in a loop while trying to acquire the lock. One way to improve performance is to insert a delay between memory references so as to limit the bandwidth (traffic) each processor can use for spinning.[3]
- Additionally, fairness can be guaranteed by queuing the lock attempts in shared memory so that they happen in order.[3]
Avoiding Locks
There are many reasons why a programmer should attempt to write programs in such a way as to avoid locks if possible as there are many problems that can arise with the use of locks. Some of them are discussed below[4]
One of the most well known issues is deadlock. This can occur when the threads are waiting to acquire the lock, but the lock would never be released. For example, there are two processes A and B and they need two methods (1 and 2) to be grabbed for completion of a task which are shared by both A and B. There is a potential deadlock situation when A grabs 1 and B grabs 2. Since both processes need one other method to reach completion, neither of them change their state. The solution to this problem is to set a condition where in process A can lock method 2 only if it has locked method 1.
Another problem with using locks is that the performance is not optimal, since a lock is often used when there is only a chance of conflict. This approach to programming yields slower performance than what might be possible with other methods. This also leads to questions of granularity, that is how much of the code should be protected under the critical section. The programmer must decide between many small (fine grain) locks or fewer, more encompassing locks. This decision can greatly effect the performance of the program.[4]
To avoid locks, lock free programming techniques like compare and swap and sequential consistency can be followed. This pattern typically involves copying a shared variable to a local variable, performing some speculative work, and attempting to publish the changes using CAS[12]:
void LockFreeQueue::push(Node* newHead)
{
for (;;)
{
// Copy a shared variable (m_Head) to a local.
Node* oldHead = m_Head;
// Do some speculative work, not yet visible to other threads.
newHead->next = oldHead;
// Next, attempt to publish our changes to the shared variable.
// If the shared variable hasn't changed, the CAS succeeds and we return.
// Otherwise, repeat.
if (_InterlockedCompareExchange(&m_Head, newHead, oldHead) == oldHead)
return;
}
}
The above code basically follows the Read-Write-Update order and makes sure that each thread has its local copy to work on and gets it updated sequentially so that the next thread has the correct value. In case the value is incorrect, the write fails.
Barrier Implementations
In many ways, barriers are simpler than locks. A barrier is simply a point in a program where one or more threads must reach before the parallel program is allowed to continue. When using barriers, a programmer does not have to be concerned with advanced topics such as fairness, that are required when programming for locks. Some of the popular barrier techniques are listed below
Fuzzy Barrier
Barriers can have a major performance impact because of two properties. Firstly, threads that have reached a barrier are forced to wait for other barriers and as a result are in an idling state. The thread is essentially performing no useful function in this state. Secondly, the execution of the barrier itself may be slow (if implemented in software), due to the fact that they may consist of several instructions that need to execute.
The fuzzy barrier aims to solve both of these issues. To increase the speed of the barrier implementation, fuzzy barriers are implemented in hardware. The other problem is to keep each thread as busy as possible for a majority of the time. This is done by extending the concept of a barrier to include a set of instructions that can be safely executed by the waiting/idling thread. By making this safe barrier region as large as possible we can ensure that almost none of the threads have to completely stall at any particular time. [14]
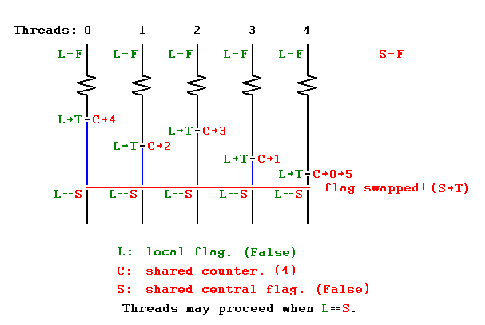
Sense-Reversal Barrier
This barrier is a centralized barrier where a single count variable protected by a lock is shared among all the threads. Each thread on reaching the barrier increments its value and waits till the value of variable has reached the number of threads for which barrier was implemented. Since all the threads are spinning around a single variable the miss rate scales quadratically with number of processors.
A sense-reversing barrier is a more elegant and practical solution to the problem of reusing barriers. A phase’s sense is a Boolean value: true for even-numbered phases and false otherwise. Each SenseBarrier object has a Boolean sense field indicating the sense of the currently executing phase. Each thread keeps its current sense as a thread-local object. Initially the barrier’s sense is the complement of the local sense of all the threads. When a thread calls await(), it checks whether it is the last thread to decrement the counter. If so, it reverses the barrier’s sense and continues. Otherwise, it spins waiting for the balancer’s sense field to change to match its own local sense.[13]
struct barrier {
shared int count;
// a Fetch&Inc/Dec() object with initial value n
// this object supports also read and write
boolean sense;
// initially FALSE;
boolean mysense[n];
// initially, psense[i] = TRUE,
// for each 1 ≤ i ≤ n.
};
void await(struct barrier *B) {
// code for process pi
int position = Get&Dec(B->count);
if (position == 1) {
B->count = n;
B->sense = B->mysense[i];
}
else {
while (B->sense!= B->mysense[i])
noop; //No operation
}
B->mysense[i] = 1-B->mysense[i];
}
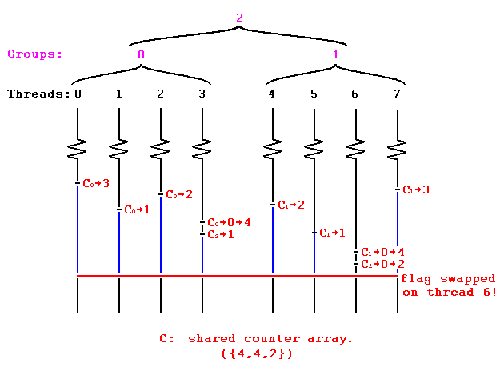
Combining Tree Barrier
This barrier is a distributed barrier where group of processors form clusters and updates value of a local variable. The local variable on reaching a value equal to number of threads updating it, proceeds to increment another variable higher in hierarchy in the combining tree. When the variable in the highest level of hierarchy in the combining tree reaches its max value it is considered that all the threads have reached the barrier and synchronization is complete.
Since in this case all the threads are updated local variables in form of smaller groups the miss rate is not as high as sense-reversal barrier. The diagram below shows the operation of combining tree barrier with threads grouped in two groups. The variables C0 and C1 are local to each group and C2 is the variable that is at higher level of hierarchy in the tree.
Another example in form of pseudo code is given below:
procedure combining_barrier combining_barrier_aux(mynode) // join the barrier sense := not sense // for next barrier procedure combining_barrier_aux(nodepointer : ^node) with nodepointer^ do if fetch_and_decrement(&count) = 1 // last to reach this node if parent != nil combining_barrier_aux(parent) count := k // prepare for next barrier nodesense := not nodesense // release waiting processors repeat until nodesense = sense
Here, each processor starts at a leaf node of the tree and the leaf count value is decreased. The last descendant to reach each node in tree gets to continue further. The processor reaching the root wakes up and retraces its path through tree and unblocks siblings at each node along path.
Tournament Barrier
In tournament barrier the threads are considered to be leaves at the end of a binary tree and each node represents a flag. Two threads compete with each other and the loser thread is allowed to set the flag and move to higher level and compete to lose with the loser thread from other section of binary tree. Thus the thread which completes last is able to set the highest flag in the binary tree. On setting the flag it indicates to all the threads that barrier has been completed and thus synchronization is achieved.
An example of tournament barrier is given as follows:
void await(boolean mySense) {
if (top) {
return;
}
else if (parent != null) {
while (flag != mySense) {};
parent.await(mySense);
partner.flag = mySense;
}
else {
partner.flag = mySense;
while (flag != mySense) {};
}
}
Here, the parent variable stores the value i.e. null if not a winner else a winner, and then waits for a partner (represented by flag) and then performs synchronization. Otherwise a natural loser is chosen and partnered with current thread.
Disseminating Barrier
In this barrier each thread maintains a record of the activity of other threads. For every round 'i' with n threads, thread A notifies thread (A + 2i) mod n. Thus after log(n) rounds all the threads are aware of the status of every other thread running and whether it has reached the barrier. Overall synchronization is achieved by implication from a carefully chosen sequence of pairwise synchronizations.
An example of this type of barrier can be found below:
for [s = 0 to stages-1] {
## there will be ceiling(log_2 p) stages
work out who my out-going partner is at stage s;
<await (arrive[partner][s] == 0);>
arrive[partner][s] = 1;
<await (arrive[myid][s] == 1);>
arrive[myid][s] = 0;
}
Here, each thread executes the same code, choosing partners for the pairwise synchronizations as a function of its own identifier and the internal iteration. Our own arrive flag is now set by an “in-coming” partner, who is distinct from our “out-going” partner (except when p=2).
Performance Evaluation
To evaluate lock performance, we can use these two criteria:[2]
Latency
Latency can be defined as the time taken to enter and exit a barrier. Ideally the latency of a barrier should be small, but for barriers that do not scale well, latency can increase as the number of threads increases.[1]
Traffic
Traffic is the communications overhead required by the barrier. Ideally barrier traffic should be low, as excess traffic limits scalability.[1]
Performance Comparison
The comparison of the performance of some of the barrier implementations have been tabulated below:
| Criteria | Sense Reversal
Centralized Barrier |
Combining Tree
Barrier |
Barrier Network
(Hardware) |
|---|---|---|---|
| Latency | O(1) | O(log p) | O(log p) |
| Traffic | O(p2) | O(p) | moved to a separate network |
References
1. David Culler, J.P. Singh and Anoop Gupta. Parallel Computer Architecture: A Hardware/Software Approach. Morgan Kaufmann. August 1998.
2. Yan Solihin. Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems. Solihin Books. August 2009.
3. Thomas E. Anderson. The Performance of Spin Lock Alternatives for Shared-memory Multiprocessors. Retrieved from here
4. http://www.statemaster.com/encyclopedia/Lock-(computer-science)
5. http://faydoc.tripod.com/cpu/cmpxchg.htm
6. http://www.cs.duke.edu/courses/fall09/cps110/slides/threads3.ppt
7. Scalability evaluation of barrier algorithms for OpenMP. https://iwomp.zih.tu-dresden.de/downloads/scalability-Nanjegowda.pdf
8. Carwyn Ball and Mark Bull. Barrier Synchronization in Java. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.97.3867&rep=rep1&type=pdf
9. http://cs.brown.edu/courses/cs176/lectures/lecture13.pptx
10.http://heather.cs.ucdavis.edu/~matloff/50/PLN/lock.pdf
11.http://www.cs.duke.edu/courses/fall09/cps110/handouts/threads3.pdf
12.Jeff Pershing. (2012, Jun 12). "An Introduction to Lock Free programming". Retreived from here
13.Maurice Herlihy and Nir Shavit. The Art of Multiprocessor Programming. Morgan Kauffman. March 03,1998
14.Rajiv Gupta. The Fuzzy Barrier: A Mechanism for High Speed Synchronization of Processors. 1989.