CSC/ECE 506 Spring 2012/ch5a ja: Difference between revisions
No edit summary |
|||
| (77 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
== Chapter 5a CSC/ECE 506 Spring 2012 / ch5a == | == Chapter 5a CSC/ECE 506 Spring 2012 / ch5a == | ||
An exploration and summary of concurrency issues as it relates to linked-list based data structures such as hash tables, trees, and graphs. This topic examines concurrency problems related to each type and possible solutions to allow for parallelization. | An exploration and summary of parallel optimization and concurrency issues as it relates to linked-list based data structures such as hash tables, trees, and graphs. This topic examines concurrency problems related to each type and possible solutions to allow for parallelization. | ||
= Introduction to Linked-List Parallel Programming = | = Introduction to Linked-List Parallel Programming = | ||
One component that tends to link together various data structures is their reliance at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket, trees have linked lists with left and right tree | One component that tends to link together various data structures is their reliance at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket in order to resolve collisions, trees have linked lists with left and right tree node paths, and graphs have linked lists to determine shortest path algorithms. | ||
But what mechanism allows us to generate parallel algorithms for these structures? | But what mechanism allows us to generate parallel algorithms for these structures? | ||
| Line 32: | Line 32: | ||
However, with linked list programming, similar to array-based programming, it becomes imperative to have some sort of locking mechanism or other parallel technique for critical sections in order to avoid race conditions. To make sure the results are correct, it is important that operations can be serialized appropriately and that data remains current and synchronized. | However, with linked list programming, similar to array-based programming, it becomes imperative to have some sort of locking mechanism or other parallel technique for critical sections in order to avoid race conditions. To make sure the results are correct, it is important that operations can be serialized appropriately and that data remains current and synchronized. | ||
In this chapter, we will explore 3 linked-list based data structures and the concurrency issues they present: hash tables, trees, and graphs. | In this chapter, we will explore 3 linked-list based data structures and the parallelization opportunities as well as the concurrency issues they present: hash tables, trees, and graphs. | ||
== Trees == | == Trees == | ||
=== Tree Intro === | |||
A tree data structure [[#References|<sup>[2]</sup>]] contains a set of ordered nodes with one parent node followed by zero or more child nodes. Typically this tree structure is used with searching or sorting algorithms to achieve log(n) efficiencies. Assuming you have a balanced tree, or a relatively equal set of nodes under each branching structure of the tree, and assuming a proper ordering structure, searches/inserts/deletes should occur far more quickly than having to traverse an entire list. | |||
=== Opportunities for Parallelization === | === Opportunities for Parallelization === | ||
One potential slowdown in a tree data structure could occur during the traversal process. Even though search/update/insert can occur in a logarithmic fashion, traversal operations such as in-order, pre-order, post-order traversals can still require a full sequence of the list to generate all output. This gives an opportunity to generate parallel code by having various portions of the traversal occur on different processors. | |||
=== Serial Code Example === | === Serial Code Example === | ||
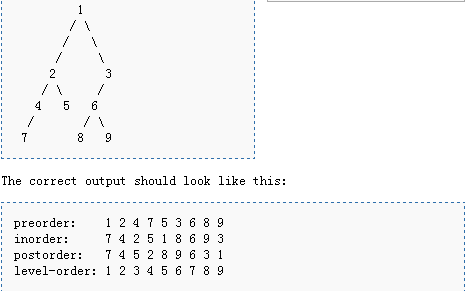
Below is a code[[#References|<sup>[ | Below is a code[[#References|<sup>[8]</sup>]] for serial tree traversal algorithms | ||
with behavior as the figure below shows: | |||
[[File: tree.PNG]] | [[File: tree.PNG]] | ||
| Line 154: | Line 158: | ||
=== Parallel Code Solution === | === Parallel Code Solution === | ||
This part we implement a parallel algorithm with the same | This part we implement a parallel algorithm with the same functionality as the serial traversal. | ||
First, we | First, we define a function NEXT[x]. The function NEXT[ x,], defining the successor of a field x, (of node x) in the Euler tour, is given as | ||
[[File: para_tree1.PNG]] | [[File: para_tree1.PNG]] | ||
| Line 178: | Line 182: | ||
in-order traversal: delete the first copy of each node if it is not | in-order traversal: delete the first copy of each node if it is not | ||
a leaf and delete the last copy of each node if it has more than one child. | a leaf and delete the last copy of each node if it has more than one child. | ||
In this fashion we have broken up the linked list of the tree into successive parts and imposed a divide-and-conquer technique to complete the traversal. | |||
== Hash Tables == | == Hash Tables == | ||
=== Hash Table Intro === | === Hash Table Intro === | ||
Hash tables[[#References|<sup>[ | Hash tables[[#References|<sup>[4]</sup>]] are very efficient data structures often used in searching algorithms for fast lookup operations. Hash tables contain a series of "buckets" that function like indexes into an array, each of which can be accessed directly using their key value. The bucket for which a piece of data will be placed is determine by a special hashing function. | ||
The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value. | The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value. | ||
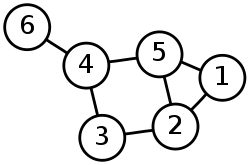
In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list.[[#References|<sup>[ | In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list.[[#References|<sup>[7]</sup>]] | ||
[[File:315px-Hash table 3 1 1 0 1 0 0 SP.svg.png]] | [[File:315px-Hash table 3 1 1 0 1 0 0 SP.svg.png]] | ||
=== | === Opportunities for Parallelization === | ||
Hash tables can be very well suited to parallel applications. For example, system code responsible for caching between multiple processors could itself be an ideal opportunity for a shared hashmap. Each processor sharing one common cache would be able to access the relevant information all in one location. | |||
This would, however, involve a good bit of synchronization, as each processor would need to wait in case a lock was being placed on a specific bucket in the cache hashmap. Unfortunately, traditional locking would be a bad solution to this problem as processors need to run very quickly. Having to wait for locks would destroy the application processing time. The need for a non-locking solution is critical to performance. | |||
In Java, the standard class utilized for hashing is the HashMap[[#References|<sup>[17]</sup>]] class. This class has a fundamental weakness though in that the entire map requires synchronization prior to each access. This causes a lot of contention and many bottlenecks on a parallel machine. | |||
Below, I will present a Java-based solution to this problem by using a ConcurrentHashMap class. This class only requires a portion of the map to be locked and reads can generally occur with no locking whatsoever. | |||
=== HashMap Code with Locking === | |||
''' Simple synchronized example to increment a counter.'''[[#References|<sup>[9]</sup>]] | |||
private Map<String,Integer> queryCounts = new HashMap<String,Integer>(1000); | |||
private '''synchronized''' void incrementCount(String q) { | |||
Integer cnt = queryCounts.get(q); | |||
if (cnt == null) { | |||
queryCounts.put(q, 1); | |||
} else { | |||
queryCounts.put(q, cnt + 1); | |||
if ( | |||
} | |||
} | } | ||
} | } | ||
The above code was written using an ordinary HashMap data structure. Notice that we use the synchronized keyword here to signify that only one thread can enter this function at any one point in time. With a really large number of threads, however, waiting to enter the synchronized operation could be a major bottleneck. | |||
''' | ''' Iterator example for synchronized HashMap.''' | ||
Map m = Collections.synchronizedMap(new HashMap()); | |||
Set s = m.keySet(); // set of keys in hashmap | |||
synchronized(m) { // synchronizing on map | |||
Iterator i = s.iterator(); // Must be in synchronized block | |||
while (i.hasNext()) | |||
foo(i.next()); | |||
} | } | ||
In the above example, we show how an iterator could be used to traverse over a map. In this case, we would need to utilize the synchronizedMap function available in the Collections interface. Also, as you may notice, once the iterator code begins we must actually synchronize on the entire map in order to iterate through the results. But what if several processors wish to iterate through at the same time? | |||
=== Parallel Code Solution === | === Parallel Code Solution === | ||
| Line 296: | Line 239: | ||
One such example in Java is the ConcurrentHashMap[[#References|<sup>[9]</sup>]], which acts as a synchronized version of the HashMap. With this structure, there is full concurrency of retrievals and adjustable expected concurrency for updates. There is, however, no locking in this data structure and retrievals will typically run in parallel along with updates/deletes. Retrievals, however, will receive all most recently completed transactions even if it cannot get the values that haven't finished being updated. This both allows for efficiency and greater concurrency. | One such example in Java is the ConcurrentHashMap[[#References|<sup>[9]</sup>]], which acts as a synchronized version of the HashMap. With this structure, there is full concurrency of retrievals and adjustable expected concurrency for updates. There is, however, no locking in this data structure and retrievals will typically run in parallel along with updates/deletes. Retrievals, however, will receive all most recently completed transactions even if it cannot get the values that haven't finished being updated. This both allows for efficiency and greater concurrency. | ||
''' | '''Parallel Counter Increment Alternative:''' | ||
private ConcurrentMap<String,Integer> queryCounts = | |||
new ConcurrentHashMap<String,Integer>(1000); | |||
private void incrementCount(String q) { | |||
Integer oldVal, newVal; | |||
do { | |||
oldVal = queryCounts.get(q); | |||
newVal = (oldVal == null) ? 1 : (oldVal + 1); | |||
} while (!queryCounts.replace(q, oldVal, newVal)); | |||
} | |||
The above code snippet represents an alternative to the serial option presented in the previous section, while also avoiding much of the locking that takes place using the synchronized functions or synchronized blocks. With ConcurrentHashMap, however, notice that we must implement some new code in order to handle the fact that a variety of inserts/updates could be running at the same time. The replace() function here acts much like a compare-and-set operation typically used with concurrent code. Basically, the value would be changed only if not equal to the previously mapped value. This is much more efficient that locking the entire function as we often do not expect unequal values. | |||
''' | '''Parallel Traversal Alternative:''' | ||
Map m = new ConcurrentHashMap(); | |||
Set s = m.keySet(); // set of keys in hashmap | |||
Iterator i = s.iterator(); // Must be in synchronized block | |||
while (i.hasNext()) | |||
foo(i.next()); | |||
In the case of a traversal, recall that ConcurrentHashMaps require to locking on read operations. Thus we can actually remove the synchronized condition here and iterate in a normal fashion. | |||
== Graphs == | == Graphs == | ||
=== Graph Intro === | === Graph Intro === | ||
A graph data structure is another type of linked-list structure that focuses on data | A graph data structure[[#References|<sup>[10]</sup>]] is another type of linked-list structure that focuses on data relationships and the most efficient ways to traverse from one node to another. For example, in a networking application, one network node may have connections to a variety of other network nodes. These nodes then also link to a variety of other nodes in the network. Using this connection of nodes, it would be possible to then find a path from one specific node to another in the chain. This could be accomplished by having each node contain a linked list of pointers to all other reachable nodes. | ||
[[File:250px-6n-graf.svg.png]] | |||
=== Opportunities for Parallelization === | |||
Graphs[[#References|<sup>[10]</sup>]] consist of a finite set of ordered pairs called edges or arcs, of certain entities called nodes or vertices. From one given vertex, one would typically want to order the different paths from one vertex to another using it's list of edges or, more than likely, would be interested in the fastest means of getting from one of these vertexes to some sort of destination vertex. | |||
Graph nodes typically will keep their list of edges in a linked list. Also, when attempting to create a shortest path algorithm on the fly, the graph will typically use a combination of a linked list to represent the path as it's being built, along with a queue that is used for each step of that process. Synchronizing all of these can be a major challenge. | |||
Much like the hash table, graphs cannot afford to be slow and must often generate results in a very efficient manner. Having to lock on each list of edges or locking on a shortest path list would really be a major obstacle. | |||
Certainly though, the need for parallel processing becomes critical when you consider, for example, that social networking has become such a major proponent of graph algorithms. Facebook now has roughly a billion users[[#References|<sup>[15]</sup>]] and each user has series of friend links that must be analyzed and examined. This list just keeps growing and growing. | |||
One of the most significant opportunities for a parallel algorithm with a graph data structure is with the traversal algorithms. We can use Breadth-First search[[#References|<sup>[16]</sup>]] as an example of this, starting from an initial node and expanding outwards until reaching the destination node. | |||
=== Breadth First Search - Serial Version === | |||
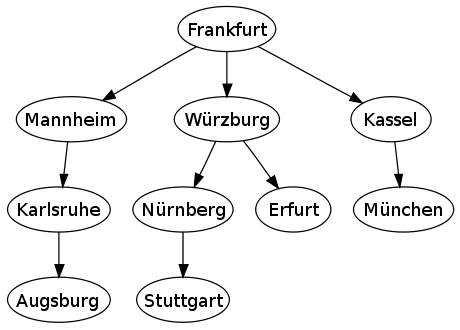
The following shows a sample of a bread first algorithm which traverses from the city of Frankfurt to Augsburg and Stuttgart Germany. In does so, the graph begins at a root node (Frankfurt) and expands outwardly to all connected nodes on each step. From there, each of those nodes proceeds to expand the search outwards until all nodes have been covered. | |||
[[File:GermanyBFS.png]][[#References|<sup>[13]</sup>]] | |||
The following code snippet[[#References|<sup>[ | The following code snippet implements a BFS search function. This function utilized coloring schemes and marks to denote that a node has been visited. It begins with an initial vertex in a queue and expands outward to all it's successors until no further elements remain unmarked.[[#References|<sup>[12]</sup>]] | ||
/ | public void search (Graph g) | ||
{ | |||
g.paint(Color.white); // paint all the graph vertices with white | |||
g.mark(false); // unmark the whole graph | |||
refresh(null); // and redraw it | |||
Vertex r = g.root(); // the root is painted grey | |||
g.paint(r, Color.gray); refresh(g.box(r)); | |||
java.util.Vector queue = new java.util.Vector(); | |||
queue.addElement(r); // and put in a queue | |||
while (!queue.isEmpty()) | |||
{ | { | ||
Vertex u = (Vertex) queue.firstElement(); | |||
queue.removeElement(u); // extract a vertex from the queue | |||
g.mark(u, true); refresh(g.box(u)); | |||
int dp = g.degreePlus(u); | |||
for (int i = 0; i < dp; i++) // look at its successors | |||
{ | |||
Vertex v = g.ithSucc(i, u); | |||
if (Color.white == g.color(v)) | |||
{ | |||
queue.addElement(v); | |||
g.paint(v, Color.gray); refresh(g.box(v)); | |||
} | } | ||
} | |||
g.paint(u, Color.black); refresh(g.box(u)); | |||
g.mark(u, false); refresh(g.box(u)); | |||
} | } | ||
} | |||
=== Parallel Solution === | |||
But could we introduce parallel mechanisms into this Breadth First search? The most logical and effective way, instead of utilizing locks and synchronized regions, is to use data parallel techniques during the traversal. This can be accomplished by having each node of a given breadth search step be sent to a separate processor. So, using the above example, instead of having Frankfurt->Mannheim followed by Frankfurt->Wurzburg followed by Frankfurt->Bassel on the same processor, Frankfurt could split out all 3 searches in a parallel fashion onto 3 different processors. Then, possible some cleanup code would be left at the end to visit any remaining untouched nodes. In a network routing applications, being able to split up the search for each IP address code would make searched significantly faster that allowing one processor to be a bottleneck. | |||
=== | Using locking pseudocode, you might have an algorithm similar to this: | ||
for all vertices u at level d in parallel do | |||
for all adjacencies v of u in parallel do | |||
dv = D[v]; | |||
if (dv < 0) // v is visited for the first time | |||
vis = fetch_and_add(&Visited[v], 1); '''LOCK''' | |||
if (vis == 0) // v is added to a stack only once | |||
D[v] = d+1; | |||
pS[count++] = v; // Add v to local thread stack | |||
fetch_and_add(&sigma[v], sigma[u]); '''LOCK''' | |||
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v '''LOCK''' | |||
if (dv == d + 1) | |||
fetch_and_add(&sigma[v], sigma[u]); '''LOCK''' | |||
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v '''LOCK''' | |||
A much better parallel algorithm is represented in the following pseudocode. Notice that each of the vertices is sent to a separate processor and send/receive operations will eventually sync up the path information. | |||
[[File:Parallel-code.PNG]][[#References|<sup>[14]</sup>]] | |||
The following graph also shows how now each of the regional sets of vertices being search can be added to the path in a parallel fashion. | |||
[[File:Parallel-graph.PNG]][[#References|<sup>[11]</sup>]] | |||
= Quiz = | = Quiz = | ||
| Line 474: | Line 372: | ||
#http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html | #http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html | ||
#http://en.wikipedia.org/wiki/Tree_%28data_structure%29 | |||
#http://oreilly.com/catalog/masteralgoc/chapter/ch08.pdf | #http://oreilly.com/catalog/masteralgoc/chapter/ch08.pdf | ||
#http://www.devjavasoft.org/code/classhashtable.html | #http://www.devjavasoft.org/code/classhashtable.html | ||
#http://osr600doc.sco.com/en/SDK_c++/_Intro_graph.html | #http://osr600doc.sco.com/en/SDK_c++/_Intro_graph.html | ||
#web.eecs.utk.edu/~berry/cs302s02/src/code/Chap14/Graph.java | #http://web.eecs.utk.edu/~berry/cs302s02/src/code/Chap14/Graph.java | ||
#http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg | #http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg | ||
#http://rosettacode.org/wiki/Talk:Tree_traversal | #http://rosettacode.org/wiki/Talk:Tree_traversal | ||
#http://www. | #http://www.javamex.com/tutorials/synchronization_concurrency_8_hashmap.shtml | ||
#http:// | #http://en.wikipedia.org/wiki/Graph_%28abstract_data_type%29 | ||
#http:// | #http://www.cc.gatech.edu/~bader/papers/PPoPP12/PPoPP-2012-part2.pdf | ||
#http://renaud.waldura.com/portfolio/graph-algorithms/classes/graph/BFSearch.java | |||
#http://en.wikipedia.org/w/index.php?title=File%3AGermanyBFS.svg | |||
#http://sc05.supercomputing.org/schedule/pdf/pap346.pdf | |||
#http://www.facebook.com/press/info.php?statistics | |||
#http://en.wikipedia.org/wiki/Breadth-first_search | |||
#http://code.wikia.com/wiki/Hashmap | |||
#http://code.wikia.com/wiki/Hashmap | |||
#http://www.shodor.org/petascale/materials/UPModules/Binary_Tree_Traversal | |||
Latest revision as of 19:59, 27 February 2013
Chapter 5a CSC/ECE 506 Spring 2012 / ch5a
An exploration and summary of parallel optimization and concurrency issues as it relates to linked-list based data structures such as hash tables, trees, and graphs. This topic examines concurrency problems related to each type and possible solutions to allow for parallelization.
Introduction to Linked-List Parallel Programming
One component that tends to link together various data structures is their reliance at some level on an internal pointer-based linked list. For example, hash tables have linked lists to support chained links to a given bucket in order to resolve collisions, trees have linked lists with left and right tree node paths, and graphs have linked lists to determine shortest path algorithms.
But what mechanism allows us to generate parallel algorithms for these structures?
For an array processing algorithm, a common technique used at the processor level is the copy-scan technique. This technique involves copying rows of data from one processor to another in a log(n) fashion until all processors have their own copy of that row. From there, you could perform a reduction technique to generate a sum of all the data, all while working in a parallel fashion. Take the following grid:[1]
The basic process for copy-scan would be to:
Step 1) Copy the row 1 array to row 2. Step 2) Copy the row 1 array to row 3, row 2 to row 4, etc on the next run. Step 3) Continue in this manner until all rows have been copied in a log(n) fashion. Step 4) Perform the parallel operations to generate the desired result (reduction for sum, etc.).
But how does this same process work in the linked list world?
With linked lists, there is a concept called pointer doubling, which works in a very similar manner to copy-scan.[1]
Step 1) Each processor will make a copy of the pointer it holds to it's neighbor. Step 2) Next, each processor will make a pointer to the processor 2 steps away. Step 3) This continues in logarithmic fashion until each processor has a pointer to the end of the chain. Step 4) Perform the parallel operations to generate the desired result.
However, with linked list programming, similar to array-based programming, it becomes imperative to have some sort of locking mechanism or other parallel technique for critical sections in order to avoid race conditions. To make sure the results are correct, it is important that operations can be serialized appropriately and that data remains current and synchronized.
In this chapter, we will explore 3 linked-list based data structures and the parallelization opportunities as well as the concurrency issues they present: hash tables, trees, and graphs.
Trees
Tree Intro
A tree data structure [2] contains a set of ordered nodes with one parent node followed by zero or more child nodes. Typically this tree structure is used with searching or sorting algorithms to achieve log(n) efficiencies. Assuming you have a balanced tree, or a relatively equal set of nodes under each branching structure of the tree, and assuming a proper ordering structure, searches/inserts/deletes should occur far more quickly than having to traverse an entire list.
Opportunities for Parallelization
One potential slowdown in a tree data structure could occur during the traversal process. Even though search/update/insert can occur in a logarithmic fashion, traversal operations such as in-order, pre-order, post-order traversals can still require a full sequence of the list to generate all output. This gives an opportunity to generate parallel code by having various portions of the traversal occur on different processors.
Serial Code Example
Below is a code[8] for serial tree traversal algorithms with behavior as the figure below shows:
procedure Tree_Traversal is
type Node;
type Node_Access is access Node;
type Node is record
Left : Node_Access := null;
Right : Node_Access := null;
Data : Integer;
end record;
procedure Destroy_Tree(N : in out Node_Access) is
procedure free is new Ada.Unchecked_Deallocation(Node, Node_Access);
begin
if N.Left /= null then
Destroy_Tree(N.Left);
end if;
if N.Right /= null then
Destroy_Tree(N.Right);
end if;
Free(N);
end Destroy_Tree;
function Tree(Value : Integer; Left : Node_Access; Right : Node_Access) return Node_Access is
Temp : Node_Access := new Node;
begin
Temp.Data := Value;
Temp.Left := Left;
Temp.Right := Right;
return Temp;
end Tree;
procedure Preorder(N : Node_Access) is
begin
Put(Integer'Image(N.Data));
if N.Left /= null then
Preorder(N.Left);
end if;
if N.Right /= null then
Preorder(N.Right);
end if;
end Preorder;
procedure Inorder(N : Node_Access) is
begin
if N.Left /= null then
Inorder(N.Left);
end if;
Put(Integer'Image(N.Data));
if N.Right /= null then
Inorder(N.Right);
end if;
end Inorder;
procedure Postorder(N : Node_Access) is
begin
if N.Left /= null then
Postorder(N.Left);
end if;
if N.Right /= null then
Postorder(N.Right);
end if;
Put(Integer'Image(N.Data));
end Postorder;
procedure Levelorder(N : Node_Access) is
package Queues is new Ada.Containers.Doubly_Linked_Lists(Node_Access);
use Queues;
Node_Queue : List;
Next : Node_Access;
begin
Node_Queue.Append(N);
while not Is_Empty(Node_Queue) loop
Next := First_Element(Node_Queue);
Delete_First(Node_Queue);
Put(Integer'Image(Next.Data));
if Next.Left /= null then
Node_Queue.Append(Next.Left);
end if;
if Next.Right /= null then
Node_Queue.Append(Next.Right);
end if;
end loop;
end Levelorder;
N : Node_Access;
begin
N := Tree(1,
Tree(2,
Tree(4,
Tree(7, null, null),
null),
Tree(5, null, null)),
Tree(3,
Tree(6,
Tree(8, null, null),
Tree(9, null, null)),
null));
Put("preorder: ");
Preorder(N);
New_Line;
Put("inorder: ");
Inorder(N);
New_Line;
Put("postorder: ");
Postorder(N);
New_Line;
Put("level order: ");
Levelorder(N);
New_Line;
Destroy_Tree(N);
end Tree_traversal;
Parallel Code Solution
This part we implement a parallel algorithm with the same functionality as the serial traversal. First, we define a function NEXT[x]. The function NEXT[ x,], defining the successor of a field x, (of node x) in the Euler tour, is given as
Note that this NEXT function does not provide the successor of the last field of the root-node r in the tour. This is because we break the tour into a linked list such that u, is the starting field and r is the terminal field, where m = no-of-chiidren[r] + 1. The proposed linked list structure can be represented as an array [I . 2n - l] of SNODEREC:

To obtain the required tree-traversals, the following rules are operated on the linked list produced by algorithm GEN-COMP-NEXT:
pre-order traversal: select the first copy of each node;
post-order traversal: select the last copy of each node;
in-order traversal: delete the first copy of each node if it is not a leaf and delete the last copy of each node if it has more than one child.
In this fashion we have broken up the linked list of the tree into successive parts and imposed a divide-and-conquer technique to complete the traversal.
Hash Tables
Hash Table Intro
Hash tables[4] are very efficient data structures often used in searching algorithms for fast lookup operations. Hash tables contain a series of "buckets" that function like indexes into an array, each of which can be accessed directly using their key value. The bucket for which a piece of data will be placed is determine by a special hashing function.
The major advantage of a hash table is that lookup times are essentially a constant value, much like an array with a known index. With a proper hashing function in place, it should be fairly rare that any 2 keys would generate the same value.
In the case that 2 keys do map to the same position, there is a conflict that must be dealt with in some fashion to obtain the correct value. One way that is relevant to linked list structures is to have a chained hash table in which a linked list is created with all values that have been placed in that particular bucket. The developer would have to not only take into account the proper bucket for the data being searched for, but also must considered the chained linked list.[7]
Opportunities for Parallelization
Hash tables can be very well suited to parallel applications. For example, system code responsible for caching between multiple processors could itself be an ideal opportunity for a shared hashmap. Each processor sharing one common cache would be able to access the relevant information all in one location.
This would, however, involve a good bit of synchronization, as each processor would need to wait in case a lock was being placed on a specific bucket in the cache hashmap. Unfortunately, traditional locking would be a bad solution to this problem as processors need to run very quickly. Having to wait for locks would destroy the application processing time. The need for a non-locking solution is critical to performance.
In Java, the standard class utilized for hashing is the HashMap[17] class. This class has a fundamental weakness though in that the entire map requires synchronization prior to each access. This causes a lot of contention and many bottlenecks on a parallel machine.
Below, I will present a Java-based solution to this problem by using a ConcurrentHashMap class. This class only requires a portion of the map to be locked and reads can generally occur with no locking whatsoever.
HashMap Code with Locking
Simple synchronized example to increment a counter.[9]
private Map<String,Integer> queryCounts = new HashMap<String,Integer>(1000);
private synchronized void incrementCount(String q) {
Integer cnt = queryCounts.get(q);
if (cnt == null) {
queryCounts.put(q, 1);
} else {
queryCounts.put(q, cnt + 1);
}
}
The above code was written using an ordinary HashMap data structure. Notice that we use the synchronized keyword here to signify that only one thread can enter this function at any one point in time. With a really large number of threads, however, waiting to enter the synchronized operation could be a major bottleneck.
Iterator example for synchronized HashMap.
Map m = Collections.synchronizedMap(new HashMap());
Set s = m.keySet(); // set of keys in hashmap
synchronized(m) { // synchronizing on map
Iterator i = s.iterator(); // Must be in synchronized block
while (i.hasNext())
foo(i.next());
}
In the above example, we show how an iterator could be used to traverse over a map. In this case, we would need to utilize the synchronizedMap function available in the Collections interface. Also, as you may notice, once the iterator code begins we must actually synchronize on the entire map in order to iterate through the results. But what if several processors wish to iterate through at the same time?
Parallel Code Solution
The key issue in a hash table in a parallel environment is to make sure any update/insert/delete sequences have been completed properly prior to attempting subsequent operations to make sure the data has been synched appropriately. However, since access speed is such a critical component of the design of a hash table, it is essential to try and avoid using too many locks for performing synchronization. Fortunately, a number of lock-free hash designs have been implemented to avoid this bottleneck.
One such example in Java is the ConcurrentHashMap[9], which acts as a synchronized version of the HashMap. With this structure, there is full concurrency of retrievals and adjustable expected concurrency for updates. There is, however, no locking in this data structure and retrievals will typically run in parallel along with updates/deletes. Retrievals, however, will receive all most recently completed transactions even if it cannot get the values that haven't finished being updated. This both allows for efficiency and greater concurrency.
Parallel Counter Increment Alternative:
private ConcurrentMap<String,Integer> queryCounts =
new ConcurrentHashMap<String,Integer>(1000);
private void incrementCount(String q) {
Integer oldVal, newVal;
do {
oldVal = queryCounts.get(q);
newVal = (oldVal == null) ? 1 : (oldVal + 1);
} while (!queryCounts.replace(q, oldVal, newVal));
}
The above code snippet represents an alternative to the serial option presented in the previous section, while also avoiding much of the locking that takes place using the synchronized functions or synchronized blocks. With ConcurrentHashMap, however, notice that we must implement some new code in order to handle the fact that a variety of inserts/updates could be running at the same time. The replace() function here acts much like a compare-and-set operation typically used with concurrent code. Basically, the value would be changed only if not equal to the previously mapped value. This is much more efficient that locking the entire function as we often do not expect unequal values.
Parallel Traversal Alternative:
Map m = new ConcurrentHashMap(); Set s = m.keySet(); // set of keys in hashmap Iterator i = s.iterator(); // Must be in synchronized block while (i.hasNext()) foo(i.next());
In the case of a traversal, recall that ConcurrentHashMaps require to locking on read operations. Thus we can actually remove the synchronized condition here and iterate in a normal fashion.
Graphs
Graph Intro
A graph data structure[10] is another type of linked-list structure that focuses on data relationships and the most efficient ways to traverse from one node to another. For example, in a networking application, one network node may have connections to a variety of other network nodes. These nodes then also link to a variety of other nodes in the network. Using this connection of nodes, it would be possible to then find a path from one specific node to another in the chain. This could be accomplished by having each node contain a linked list of pointers to all other reachable nodes.
Opportunities for Parallelization
Graphs[10] consist of a finite set of ordered pairs called edges or arcs, of certain entities called nodes or vertices. From one given vertex, one would typically want to order the different paths from one vertex to another using it's list of edges or, more than likely, would be interested in the fastest means of getting from one of these vertexes to some sort of destination vertex.
Graph nodes typically will keep their list of edges in a linked list. Also, when attempting to create a shortest path algorithm on the fly, the graph will typically use a combination of a linked list to represent the path as it's being built, along with a queue that is used for each step of that process. Synchronizing all of these can be a major challenge.
Much like the hash table, graphs cannot afford to be slow and must often generate results in a very efficient manner. Having to lock on each list of edges or locking on a shortest path list would really be a major obstacle.
Certainly though, the need for parallel processing becomes critical when you consider, for example, that social networking has become such a major proponent of graph algorithms. Facebook now has roughly a billion users[15] and each user has series of friend links that must be analyzed and examined. This list just keeps growing and growing.
One of the most significant opportunities for a parallel algorithm with a graph data structure is with the traversal algorithms. We can use Breadth-First search[16] as an example of this, starting from an initial node and expanding outwards until reaching the destination node.
Breadth First Search - Serial Version
The following shows a sample of a bread first algorithm which traverses from the city of Frankfurt to Augsburg and Stuttgart Germany. In does so, the graph begins at a root node (Frankfurt) and expands outwardly to all connected nodes on each step. From there, each of those nodes proceeds to expand the search outwards until all nodes have been covered.
The following code snippet implements a BFS search function. This function utilized coloring schemes and marks to denote that a node has been visited. It begins with an initial vertex in a queue and expands outward to all it's successors until no further elements remain unmarked.[12]
public void search (Graph g)
{
g.paint(Color.white); // paint all the graph vertices with white
g.mark(false); // unmark the whole graph
refresh(null); // and redraw it
Vertex r = g.root(); // the root is painted grey
g.paint(r, Color.gray); refresh(g.box(r));
java.util.Vector queue = new java.util.Vector();
queue.addElement(r); // and put in a queue
while (!queue.isEmpty())
{
Vertex u = (Vertex) queue.firstElement();
queue.removeElement(u); // extract a vertex from the queue
g.mark(u, true); refresh(g.box(u));
int dp = g.degreePlus(u);
for (int i = 0; i < dp; i++) // look at its successors
{
Vertex v = g.ithSucc(i, u);
if (Color.white == g.color(v))
{
queue.addElement(v);
g.paint(v, Color.gray); refresh(g.box(v));
}
}
g.paint(u, Color.black); refresh(g.box(u));
g.mark(u, false); refresh(g.box(u));
}
}
Parallel Solution
But could we introduce parallel mechanisms into this Breadth First search? The most logical and effective way, instead of utilizing locks and synchronized regions, is to use data parallel techniques during the traversal. This can be accomplished by having each node of a given breadth search step be sent to a separate processor. So, using the above example, instead of having Frankfurt->Mannheim followed by Frankfurt->Wurzburg followed by Frankfurt->Bassel on the same processor, Frankfurt could split out all 3 searches in a parallel fashion onto 3 different processors. Then, possible some cleanup code would be left at the end to visit any remaining untouched nodes. In a network routing applications, being able to split up the search for each IP address code would make searched significantly faster that allowing one processor to be a bottleneck.
Using locking pseudocode, you might have an algorithm similar to this:
for all vertices u at level d in parallel do
for all adjacencies v of u in parallel do
dv = D[v];
if (dv < 0) // v is visited for the first time
vis = fetch_and_add(&Visited[v], 1); LOCK
if (vis == 0) // v is added to a stack only once
D[v] = d+1;
pS[count++] = v; // Add v to local thread stack
fetch_and_add(&sigma[v], sigma[u]); LOCK
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v LOCK
if (dv == d + 1)
fetch_and_add(&sigma[v], sigma[u]); LOCK
fetch_and_add(&Pcount[v], 1); // Add u to predecessor list of v LOCK
A much better parallel algorithm is represented in the following pseudocode. Notice that each of the vertices is sent to a separate processor and send/receive operations will eventually sync up the path information.
The following graph also shows how now each of the regional sets of vertices being search can be added to the path in a parallel fashion.
Quiz
1. Describe the copy-scan technique.
2. Describe the pointer doubling technique.
3. Which concurrency issues are of the most concern in a tree data structure?
4. What is the alternative to using a copy-scan technique in pointer-based programming?
5. Which concurrency issues are of the most concern with hash table data structures?
6. Which concurrency issues are of the most concern with graph data structures?
7. Why would you not want locking mechanisms in hash tables?
8. What is the nature of the linked list in a tree structure?
9. Describe a parallel alternative in the tree data structure.
10. Describe a parallel alternative in a graph data structure.
References
- http://people.engr.ncsu.edu/efg/506/s01/lectures/notes/lec8.html
- http://en.wikipedia.org/wiki/Tree_%28data_structure%29
- http://oreilly.com/catalog/masteralgoc/chapter/ch08.pdf
- http://www.devjavasoft.org/code/classhashtable.html
- http://osr600doc.sco.com/en/SDK_c++/_Intro_graph.html
- http://web.eecs.utk.edu/~berry/cs302s02/src/code/Chap14/Graph.java
- http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg
- http://rosettacode.org/wiki/Talk:Tree_traversal
- http://www.javamex.com/tutorials/synchronization_concurrency_8_hashmap.shtml
- http://en.wikipedia.org/wiki/Graph_%28abstract_data_type%29
- http://www.cc.gatech.edu/~bader/papers/PPoPP12/PPoPP-2012-part2.pdf
- http://renaud.waldura.com/portfolio/graph-algorithms/classes/graph/BFSearch.java
- http://en.wikipedia.org/w/index.php?title=File%3AGermanyBFS.svg
- http://sc05.supercomputing.org/schedule/pdf/pap346.pdf
- http://www.facebook.com/press/info.php?statistics
- http://en.wikipedia.org/wiki/Breadth-first_search
- http://code.wikia.com/wiki/Hashmap
- http://code.wikia.com/wiki/Hashmap
- http://www.shodor.org/petascale/materials/UPModules/Binary_Tree_Traversal