CSC/ECE 506 Spring 2012/1c 12: Difference between revisions
| (208 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
This article is a discussion on systolic arrays and their relation to MISD architectures. Since very little information and no examples are available on MISD, this article gives a brief introduction using Flynn's 1966 taxonomy on the subject. The article then presents a brief introduction to systolic arrays and discusses their mathematical uses and real-world engineering uses as examples. From these applications, the article shows where the claim that systolic arrays are examples of MISD is acceptable, and where it stretches the argued definition of MISD. | |||
==MISD== | ==MISD== | ||
[http://en.wikipedia.org/wiki/Michael_J._Flynn Micheal J. Flynn] introduced the idea of an [http://en.wikipedia.org/wiki/MISD MISD (Multiple Instruction, Single Data)] computer architectures in his original [http://en.wikipedia.org/wiki/Flynn%27s_taxonomy taxonomy] in 1966.[[#References|<sup>[1]</sup>]] | [http://en.wikipedia.org/wiki/Michael_J._Flynn Micheal J. Flynn] introduced the idea of an [http://en.wikipedia.org/wiki/MISD MISD (Multiple Instruction, Single Data)] computer architectures in his original [http://en.wikipedia.org/wiki/Flynn%27s_taxonomy taxonomy] in 1966.[[#References|<sup>[1]</sup>]] The basic Flynn's architecture is as below | ||
[[image:Taxonomy.jpg|thumb|center|400px|alt=Flynn's Taxonomy.|From the notes of Cornell Theory center [[#References|<sup>[30]</sup>]].]] | |||
===The MISD Architecture=== | ===The MISD Architecture=== | ||
[http://www.ece.ncsu.edu/people/solihin Dr. Yan Solihin] defines MISD as "..an architecture in which multiple processing elements execute from different instruction streams, and data is passed from one processing element to the next."[[#References|<sup>[2]</sup>]] He also notes that MISD architectures are restricted to certain types of computations due to the requirement of data-passing between processing elements.[[#References|<sup>[2]</sup>]] Each processing element executes different instructions on the data stream.[[#References|<sup>[3]</sup>]] Every time the data is processed by a processing element, we can always | [http://www.ece.ncsu.edu/people/solihin Dr. Yan Solihin] defines MISD as "..an architecture in which multiple processing elements execute from different instruction streams, and data is passed from one processing element to the next."[[#References|<sup>[2]</sup>]] He also notes that MISD architectures are restricted to certain types of computations due to the requirement of data-passing between processing elements.[[#References|<sup>[2]</sup>]] Each processing element executes different instructions on the data stream.[[#References|<sup>[3]</sup>]] Every time the data is processed by a processing element, we can always argue that the data is no longer the original data introduced at the start of the stream.[[#References|<sup>[4]</sup>]] | ||
[[image:NCSU Misd.jpg|thumb|center|400px|alt=MISD computer architecture outline.|From NCSU CSC/ECE 506 Spring 2012 Lecture 1 notes[[#References|<sup>[5]</sup>]].]] | [[image:NCSU Misd.jpg|thumb|center|400px|alt=MISD computer architecture outline.|From NCSU CSC/ECE 506 Spring 2012 Lecture 1 notes[[#References|<sup>[5]</sup>]].]] | ||
| Line 20: | Line 24: | ||
===MISD Computers=== | ===MISD Computers=== | ||
While it is widely believed that no actual MISD computer exists in practice, it is controversially argued that a [http://en.wikipedia.org/wiki/Systolic_array systolic array] is the most common example of MISD[[#References|<sup>[6]</sup>]]. | While it is widely believed that no actual MISD computer exists in practice, it is controversially argued that a [http://en.wikipedia.org/wiki/Systolic_array systolic array] is the most common example of MISD[[#References|<sup>[6]</sup>]]. One often cited example of MISD (most notable from the [http://en.wikipedia.org/wiki/MISD MISD wiki article]) is the space shuttle flight-control computers. The authors of this article found no source material backing this claim (even the MISD wiki is awaiting a citation on the claim), and found very little on the actual architectures of those computers. The closest assumption for the claim the authors of this article could find is the system designed for redundancy management/fault tolerance[[#References|<sup>[29]</sup>]], which [[#References|[26]]] discusses the uses of systolic array in fault-tolerant systems. | ||
Some arguments exist that pipelined vector processors could be considered an example of MISD architecture due to the fact that a different operation is performed on the data stream as it flows from stage to stage[[#References|<sup>[6]</sup>]]. The argument against this idea is that individual processing elements in each stage do not technically fetch their operations from an instruction cache[[#References|<sup>[6]</sup>]], but are more similar to a function specific, or [http://en.wikipedia.org/wiki/Application-specific_integrated_circuit ASIC], chip. | Some arguments exist that pipelined vector processors could be considered an example of MISD architecture due to the fact that a different operation is performed on the data stream as it flows from stage to stage[[#References|<sup>[6]</sup>]]. The argument against this idea is that individual processing elements in each stage do not technically fetch their operations from an instruction cache[[#References|<sup>[6]</sup>]], but are more similar to a function specific, or [http://en.wikipedia.org/wiki/Application-specific_integrated_circuit ASIC], chip. | ||
| Line 26: | Line 30: | ||
One application that exists for MISD VLSI architectures are applications which require multiple pattern matching in large data streams that lack any preprocessed indexes for lookups[[#References|<sup>[8]</sup>]]. This research presents a set of recursive query semantics: "concatenation of basic strings and patterns, alphanumerical comparisons of simple strings, boolean operations on subexpressions, and hamming distance filtering"[[#References|<sup>[12]</sup>]], and then explains that the recursion process of the semantics is best understood as a "..recursion tree where the result is found by propagating the results from the leaf nodes...to the root of the tree"[[#Reference|<sup>[12]</sup>]]. | One application that exists for MISD VLSI architectures are applications which require multiple pattern matching in large data streams that lack any preprocessed indexes for lookups[[#References|<sup>[8]</sup>]]. This research presents a set of recursive query semantics: "concatenation of basic strings and patterns, alphanumerical comparisons of simple strings, boolean operations on subexpressions, and hamming distance filtering"[[#References|<sup>[12]</sup>]], and then explains that the recursion process of the semantics is best understood as a "..recursion tree where the result is found by propagating the results from the leaf nodes...to the root of the tree"[[#Reference|<sup>[12]</sup>]]. | ||
Recently, [http://en.wikipedia.org/wiki/Stanford_university Stanford University] and [http://www.maxeler.com/content/frontpage/ Maxeler Technologies] have been working on acceleration methodologies that benefit from combining different computer architectures. One of the proposed methodologies based on FPGA arrays uses SIMD for multiple data strips until the pin bandwidth limits the acceleration, then switches to an MISD-style pipeline of the FPGA arrays until acceleration is limited by circuit limitations[[#References|<sup>[13]</sup>]]. | Recently, [http://en.wikipedia.org/wiki/Stanford_university Stanford University] and [http://www.maxeler.com/content/frontpage/ Maxeler Technologies] have been working on acceleration methodologies that benefit from combining different computer architectures. One of the proposed methodologies based on FPGA arrays uses SIMD for multiple data strips until the pin bandwidth limits the acceleration, then switches to an MISD-style pipeline of the FPGA arrays until acceleration is limited by circuit limitations[[#References|<sup>[13]</sup>]]. Similar research on implementing MISD pipelines via FPGAs for biologicaly-inspired machine vision ([http://szeliski.org/Book/ VI]-like) algorithms has been introduced in [[#References|[18]]]. | ||
==Systolic Array== | ==Systolic Array== | ||
The [http://en.wikipedia.org/wiki/Systolic_array systolic array] was first introduced in 1978 by Kung and Leiserson.[[#References|<sup>[20]</sup>]] | |||
===What is a Systolic Array?=== | ===What is a Systolic Array?=== | ||
"A systolic array is an arrangement of processors in an array (often rectangular) where data flows synchronously across the array between neighbors"[[#References|<sup>[7]</sup>]] Systolic arrays have [http://en.wikipedia.org/wiki/Data_processing_system data processing units (DPU) ] arranged in the form an matrix such that they are connected to their neighbors in the form of a mesh.[[#References|<sup>[9]</sup>]] | |||
The two models of systolic arrays are shown below: | |||
[[File:Systolic2-arch.jpg|frame|center|500px|alt=Systolic Array Architecture1 .|From systolic array and their architecture by Jonathan break[[#References|<sup>[23 ]</sup>]].]] | |||
The above diagram represents a systolic array where each DPU performs a specific operation on the data which can be input/output from an external source in the case of embedded systems or could be system generated by a [http://en.wikipedia.org/wiki/Auto-sequencing_memory auto sequencing memory unit]. Each DPU performs a different computation based on the instruction set given to it and takes in data from the top or the left and then outputs it to it's right or below. A systolic array may or may not have local memory based on the application it is being used for. | |||
[[File: | [[File:Systolic_array_mul.jpg|thumb|center|600px|alt=Systolic Array Architecture2 .| Matrix multiplication using systolic array[[#References|<sup>[10]</sup>]].]] | ||
An example of an application of systolic array is a matrix multiplication. The systolic array can have a 4X4 mesh to multiply two 4X4 matrices where the data of all the rows and columns to be multiplied can be entered as the input into each DPU and the instruction executed by each DPU would be to multiply the incoming stream of numbers and add them to a previous value stored in it if there is any. The final output that is the resultant matrix would be the values stored in each DPU. | An example of an application of systolic array is a matrix multiplication. The systolic array can have a 4X4 mesh to multiply two 4X4 matrices where the data of all the rows and columns to be multiplied can be entered as the input into each DPU and the instruction executed by each DPU would be to multiply the incoming stream of numbers and add them to a previous value stored in it if there is any. The final output that is the resultant matrix would be the values stored in each DPU. | ||
The function of each DPU in the above example is as follows | |||
1)Each DPU takes as input a and b | |||
2)Multiplies a ,b | |||
3)It adds the value of multiplication to a previous value and stores the value of addition | |||
4)Sends value of a to DPU<sub>ij+1</sub> if j is not 4 | |||
5)Sends value of b to DPU<sub>i+1j</sub> if i is not 4 | |||
Systolic arrays can be used to make algorithms involving a lot of parallel computation much easier. "Systolic array processors have been known to be extremely efficient at executing the class of algorithms that exhibit tight coupling between neighboring cells via data transfers in an N-dimensional model space" [[#References|<sup>[11]</sup>]] | Systolic arrays can be used to make algorithms involving a lot of parallel computation much easier. "Systolic array processors have been known to be extremely efficient at executing the class of algorithms that exhibit tight coupling between neighboring cells via data transfers in an N-dimensional model space."[[#References|<sup>[11]</sup>]] Though the size of the array does affect the performance. Small systolic arrays present timing issues, limitations on bus width and chip pins, as well as pipeline drain caused by interruptions in the data flow. Approaches discussed to resolve these issues were problem partition (either the specified algorithm or the data array), array emulation (time-sharing a small array's processors to mimic a larger array more properly suited to the specified algorithm), and software based scheduling programs.[[#References|<sup>[15]</sup>]] The size of a systolic array is primarily determined by the number of individual processing elements and the total computation time needed for the specific algorithm, but then this also depends on the length of the loop and the transformation matrix of the specific algorithm.[[#References|<sup>[17]</sup>]] | ||
===Applications of Systolic Arrays=== | ===Applications of Systolic Arrays=== | ||
Various complex systems that can be optimized with systolic arrays include: | |||
<ul> | <ul> | ||
<li> | <li> [http://en.wikipedia.org/wiki/Deblocking_filter_(video) Video Filtering] </li> | ||
<li> | <li> [http://en.wikipedia.org/wiki/Data_compression Data Compression] </li> | ||
<li> | <li> [http://en.wikipedia.org/wiki/Image_processing Image Processing] </li> | ||
<li> | <li> [http://en.wikipedia.org/wiki/Signal_processing Signal Processing] </li> | ||
<li> [http://en.wikipedia.org/wiki/Category:Computer_graphics_algorithms Graphic Algorithms] </li> | |||
<li> [http://en.wikipedia.org/wiki/Sequence_alignment Biological Sequence Comparison] </li> | |||
<li> | |||
<li> | |||
</ul> | </ul> | ||
Systolic arrays are useful in these applications due to their usefulness in efficiently accelerating computation-intense problems ("..problems where the amount of computation required to solve the problem is very large compared to the amount of input/output"[[#References|<sup>[25]</sup>]]) like vector-matrix [http://en.wikipedia.org/wiki/Multiplication multiplication], [http://en.wikipedia.org/wiki/Discrete_Fourier_transform Discrete Fourier Transforms (DFT)], [http://en.wikipedia.org/wiki/Fast_Fourier_transform Fast Fourier Transforms (FFT)], [http://en.wikipedia.org/wiki/Convolution convolution], [http://en.wikipedia.org/wiki/Dynamic_time_warping Dynamic Time Warping (DTW)], and [http://en.wikipedia.org/wiki/Differential_equation differential equations]. [[#References|[26]]] also presents data supporting the use of systolic array for algorithm-based [http://en.wikipedia.org/wiki/Fault-tolerant_system fault tolerant systems], using [http://en.wikipedia.org/wiki/Laplace's_equation Laplace's equation] as an example. | |||
====[http://en.wikipedia.org/wiki/Discrete_Fourier_transform Discrete Fourier Transforms]==== | |||
= | [[File:DFT-image2.jpg|frame|right|10px|alt=Systolic Array Architecture1 .|Systolic Array architecture as used in Efficient One-Dimensional Systolic Array Realization of the Discrete Fourier Transform break[[#References|<sup>[19 ]</sup>]].]] | ||
The advancement of VLSI systolic arrays became the first preference to use for the digital processing algorithms as systolic array's could solve complicated problems by just using array which are similar.A [http://en.wikipedia.org/wiki/Discrete_Fourier_transform Discrete Fourier transform (DFT)] could be efficiently calculated using a one dimensional systolic array which was formed by using a modification of [http://en.wikipedia.org/wiki/Goertzel_algorithm First order Goertzel algorithm]. | |||
The picture on the right shows a systolic array for a 3 point DFT.The data is sent continuously into the array and a each cell takes in a sample to calculate one DFT sample.Each cell has an adder and PROM multiplier .After calculating one sample the cells send the data to their neighbors and hence a new sample is available at each cell again for computation.The input given is {a(0),a(1),a(2)} ,{b(0),b(1),b(2)}, {c(0),c(1),c(2)} and the output DFT vectors are {A(0),A(1),A(2)} , {B(0),B(1),B(2)} , {C(0),C(1),C(2)}. | |||
"Each cell accumulates partial terms of one particular DFT sample" [[#References|<sup>[19 ]</sup>]] | |||
==== | ====[http://en.wikipedia.org/wiki/Fast_Fourier_transform Fast Fourier transform]==== | ||
= | [[#References|<sup>[28]</sup>]] uses a special type of systolic array called Tagged Systolic Array(TSA)to solve Fast Fourier Transform , as they cannot be represented in the form of [http://dl.acm.org/citation.cfm?id=321418 uniform recurrence equations] which makes the formulation of a simple systolic array to solve it difficult. | ||
In a TSA "tags are attached to the results of a particular computation for properly routing them to other processing elements (PES)/DPU's where the result of that particular computation is required." [[#References|<sup>[28]</sup>]] It uses the communication links of only the nearest neighbors to send its data. | |||
To design a systolic array for an FFT the index points should be mapped to a smaller number of processing elements which should be connected. But the problem arises as the PE's which generate the variable and the PE which use the variable might not necessarily be neighbors in this case and also the location of destination PE might change with time and location of the source." In such cases tags (evaluated based on location and time) are attached to the data generated at the source PE for proper routing of data. This type of architecture that uses tags for data routing is called a Tagged Systolic Array (TSA)" | |||
The TSA for FFT is a linear array and uses tags to pass data. | |||
[[File:FFT-image.jpg|thumb|center|600px|alt=Systolic Array Architecture2 .| Tagged systolic array for FFT[[#References|<sup>[28 ]</sup>]].]] | |||
Each PE stores two kinds of data one for computation and the other is an intermediate result as well as two tags which are always constant. "The tag of a data is checked at a PE to determine its further direction of movement or to decide whether the data is required at the PE itself." If the data is required by the PE it stores it else it forwards it to its neighboring PE. | |||
All the PE's in the pipeline are divided into various groups such that each group is used for calculating a different stage of a FFT. PE's in one group perform a similar operation. In the figure "PE1 performs the computations of stage 1, PE2 & PE3 perform computations of stage 2 and PE4, PE5,PE6 & PE7 are responsible for stage 3 computation."[[#References|<sup>[28]</sup>]] | |||
==== | ====[http://en.wikipedia.org/wiki/Convolution Convolution]==== | ||
In 2003, the idea of a super-systolic array was introduced by Jae-Jin Lee and Gi-Yong Son. [[#References|[16]]] explains that a super-systolic array involves making cells of systolic array themselves a systolic array and defines the use of a super-systolic array for convolution as "..a logical systolic array in a sense that the array assumes all operation to complete in a unit delay to maintain rhythmic data flow." For the convolution problem in [[#Reference|[16]]], each cell in the systolic array is capable of performing multiplication and addition. It is the multiplication process that benefits highly from systolization, and is implemented as a systolic array in itself. Converting the cells of systolic array into systolic array themselves results in higher degrees of concurrency and lower resource consumption[[#References|<sup>[16]</sup>]]. | |||
====Differential Equations==== | [[image:Convolution-pic systolic array.jpg|framed|center|500px|alt=MISD computer architecture outline.|Synthesized schematic for systolic multiplier in [[#References|[16]]].]] | ||
[[#References|[22]]] introduces the concept of the moment-based systolic array of convolutions, which generally decreased to total delay associated with convolution implementations. | |||
[[image:Moment based convoluion.jpg|framed|center|300px|alt=MISD computer architecture outline.|Moment-based systolic array of convolutions from [[#References|[22]]].]] | |||
====[http://en.wikipedia.org/wiki/Dynamic_time_warping Dynamic Time Warping (DTW)]==== | |||
[[#References|[24]]] introduces DTW as an array of identical processing units, each designed to compute local distance and global measurements of dissimilarity. Systolic arrays were discovered in [[#References|[24]]] to reduce design costs and speed up processing time by processing a new reference pattern immediately following the completion of the previous reference pattern. [[#References|[24]]] found that by precisely defining the kind of interconnections between each individual processing unit to suit particular application requirements bypassed the problem of only half the processing units working only half the time, thus they were able to obtain optimal performance for individual circuits and the system as a whole. Although, for [[#References|[24]]], the individual processing units themselves are [http://en.wikipedia.org/wiki/Application-specific_integrated_circuit ASIC] to the [http://en.wikipedia.org/wiki/Dynamic_time_warping DTW] algorithm being implemented. | |||
====[http://en.wikipedia.org/wiki/Differential_equation Differential Equations (DEQ)]==== | |||
[[#References|[25]]] discusses the use of systolic array for real-time simulations of industrial systems. They propose a system of three DEQs (N=3, four terms). The systolic array operates through each function, evaluating the four terms (simultaneously) and feeding the results back into itself. [[#References|[25]]] explains that if the system is linear, the initial elements of the [http://en.wikipedia.org/wiki/Matrix_calculus differential matrix] are constant throughout the simulation; but if the system is nonlinear, new matrix elements are computed and loaded into the proper nodes of the systolic array. The proposed systolic array in [[#References|[25]]] is seemingly re-configurable, in that as N changes, the array can adjust. | |||
[[image:Diff-eq-image.jpg|framed|right|300px|alt=MISD computer architecture outline.| "Systolic array for real-time simulation of dynamic systems (N = 3) of DEQs" [[#References|<sup>[25]</sup>]].]] | |||
[[#References|[27]]] discusses use of the [http://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods Runge-Katta method] to solve ordinary dynamic equations (ODE) and partial dynamic equations (PDE) within the Yau filtering system. The ability to perform parallel computations on systolic architectures became one advantage for using the Runge-Katta method. [[#References|[27]]] is another example of the use of systolic array for matrix-vector multiplication, as well as vector addition. | |||
==Systolic Array vs. MISD== | |||
If relating to an MISD architecture, a systolic array is "..a network of small computing elements connected in a regular grid. All the elements are controlled by a global clock. On each cycle, an element will read a piece of data from one of its neighbors, perform a simple operation (e.g. add the incoming element to a stored value), and prepare a value to be written to a neighbor on the next step"[6]. This of course relates to the idea that typically the inner processing units (or nodes) of a systolic array do not access memory or buffers, but pass the data from node-to-node via registers. This relates to Flynn's taxonomy of MISD architecture correctly in that only the first and last processing units (nodes) will access the original data stream. Conversely, [[#References|[21]]] describes a systolic array system quite unlike an MISD architecture by emphasizing that the systolic array pipeline reduces the need for control logic, control signal generation, and the cost of [http://en.wikipedia.org/wiki/Finite-state_machine FSM] design. | |||
If a systolic array is not designed with a local memory, the individual processing units are then generally designed to be non-programmable (basically [http://en.wikipedia.org/wiki/Application-specific_integrated_circuit ASIC]) and data is then introduced to the systolioc array through an outside shared memory controller (perhaps even through buffers to ease memory traffic)[[#References|<sup>[15]</sup>]]. If designed without a local memory, then, a systolic array does not fit Flynn's taxonomy of MISD architecture: the data stream is still the only means of interaction between the individual processing units, but those individual processing units lack individual intruction memories. It could be argued to mimic [http://en.wikipedia.org/wiki/SISD SISD (single instruction, single data)] at this point, since the processing units themself are generally application-specific. If a systolic array is designed with a local memory, it gains not only the ability to fetch data from that local memory[[#References|<sup>[15]</sup>]], but also instructions. It could: a) have a local instruction memory, in which a program fetches and transmits instructions to each individual processing unit (on the assumption that each of those units is beyond application-specific), or b) attempt to mimic Flynn's MISD taxonomy and grant each of those individiaul processing units an individual instruction memory. The second option does present much overhead, and if not necessarily application or algorithm dependant, will be quite costly for no appearnt reason. | |||
Consistently we see that one major design characteristic that either places a systolic array in the MISD list or forces it to stretch the definition is the idea of application-specification, or being problem specific. The MISD architecture Flynn describes are individual processing units that are typically the same as it's neighbors,[[#References|<sup>[14]</sup>]] which we presume are guided by an [http://en.wikipedia.org/wiki/Instruction_set ISA (instruction set architecture)] capable of identification and execution of multiple operations. To achieve a systolic array that is more purely MISD, it must be re-configurable in some way. [[#References|[17]]] defines a re-configurable systolic array as one "..that can be adapted to computing multiple problems through either software or hardware configuration, or both." [[#References|[17]]] shows that one such way is to design the systolic array architecture such that two or more algorithms can mapped to a single re-configurable systolic array. This is done in two steps: compute individual algorithms one at a time with their proper control settings, then extend the array using time or space redundancy to compute multiple algorithms simultaneously. The space-time mapping procedure in [[#References|[17]]] is achieved by mapping different algorithms to individual systolic arrays using one common transformation matrix, then extracting common parts of each circuit within processing units and merging those arrays into one re-configurable systolic array. | |||
One final argument for the claim that calling systolic array an MISD architecture is stretching the definition of MISD is that generally, for most applications, both the data and instruction streams for systolic array are serial. This conflicts with Flynn's taxonomy of MISD because he classifies it as an example of parallel computer architecture[[#References|<sup>[14]</sup>]] in which the instruction stream is parallel. | |||
==References== | ==References== | ||
| Line 96: | Line 146: | ||
<li> [http://www.phy.ornl.gov/csep/ca/node14.html 3.1.3 MISD Computers] </li> | <li> [http://www.phy.ornl.gov/csep/ca/node14.html 3.1.3 MISD Computers] </li> | ||
<li> Laiq hasan,Yahya M.Khawaja,Abdul Bais,"A Systolic Array Architecture for the Smith-Waterman Algorithm with High Performance Cell Design" in IADIS European Conference Data Mining, 2008, pp. 37 </li> | <li> Laiq hasan,Yahya M.Khawaja,Abdul Bais,"A Systolic Array Architecture for the Smith-Waterman Algorithm with High Performance Cell Design" in IADIS European Conference Data Mining, 2008, pp. 37 </li> | ||
<li> Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, | <li> Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, Vol. 12, No. 7, pp. 727, July 2004. </li> | ||
<li> [http://en.wikipedia.org/wiki/Systolic_array Systolic array]</li> | <li> [http://en.wikipedia.org/wiki/Systolic_array Systolic array]</li> | ||
<li> [http://en.wikipedia.org/wiki/File:Systolic_array.jpg Systolic array architecture]</li> | <li> [http://en.wikipedia.org/wiki/File:Systolic_array.jpg Systolic array architecture]</li> | ||
<li> Robert E. Morley, Jr.Thomas J. Sullivan ,"A Massively Parallel Systolic Array Processor System," in Electronic Systems and Signals Research Laboratory,Department of Electrical Engineering,Washington University, pp | <li> Robert E. Morley, Jr.Thomas J. Sullivan ,"A Massively Parallel Systolic Array Processor System," in Electronic Systems and Signals Research Laboratory,Department of Electrical Engineering,Washington University, pp. 217. </li> | ||
<li> Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, | <li> Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, Vol. 12, No. 7, pp. 728, July 2004. </li> | ||
<li> Michael Flynn, R. Dimond, O. Mencer, O. Pell, "Finding Speedup in Parallel Processors," in International Symposium on Parallel and Distributed Computing | <li> Michael Flynn, R. Dimond, O. Mencer, O. Pell, "Finding Speedup in Parallel Processors," in International Symposium on Parallel and Distributed Computing, pp. 3, 2008. </li> | ||
<li> Michael J. Flnn, "Very High-Speed Computing Systems," Proceedings of the IEEE, | <li> Michael J. Flnn, "Very High-Speed Computing Systems," Proceedings of the IEEE, Vol. 54, No. 12, pp.1908, December 1966. </li> | ||
<li> Henry Y. H. Chuang, Ling Chen, "A General Approach to Solving Arbitrarily Large Problems in a Fixed Size Systolic Array," in Proceedings of the Twenty-First Annual Hawaii International Conference on System Sciences, Vol. 2, Software Track, pp. 195-204, 1988. </li> | |||
<li> Jae-Jin Lee, Gi-Yong Song, "Implementation of the Super-Systolic Array for Convolution," in Proceedings of the ASP-DAC Asia and South Pacific Design Automation Conference, pp. 491-494, 2003. </li> | |||
<li> Wei Jin, Cang N. Zhang, and Hua Li, "Mapping Multiple Algorithms into a Reconfigurable Systolic Array," in Canadian Conference on Electrical and Computer Engineering, pp. 1187-1191, 2008. </li> | |||
<li> Vinay Sriram, David Cox, Kuen Hung Tsoi, and Wayne Luk, "Towards an Embedded Biologically-Inspired Machine Vision Processor," in International Conference on Field-Programmable Technology (FPT), pp. 273-278, 2010. </li> | |||
<li> J.A. Beraldin, Tyseer Aboulnasar, and Willem Steenart, "Efficient One-Dimensional Systolic Array Realization of the Discrete Fourier Transform," in IEEE Transactions of circuits and systems, Vol. 36, No. 1, pp. 95-100, January 1989. </li> | |||
<li> H. Kung, and C. Leiserson, “Systolic arrays (for VLSI),” in Sparse matrix proceedings, 1978. Society for Industrial & Appl. Mathematics, pp. 256–309, 1979. </li> | |||
<li> Liang Lu, Weiqiang Liu, Maire O’Neill, and Earl E. Swartzlander Jr., "QCA Systolic Array Design," in IEEE Transactions on Computers, Issue 99, December 2011. </li> | |||
<li> Jianguo Liu, Chao Pan, and Zhenbing Li, "Novel Convolutions using First-order Moments, in IEEE Transactions on Computers, Issue 99, July 2011. </li> | |||
<li> [http://coefs2.njit.edu/labmanuals/ece459/images/array.gif Matrix Multiplication using systolic array ] | |||
<li> F. Jutand, N. Dennassieux, D. Vicard, and G Chollet, "VLSI Architectures For Dynamic Time Warping Using Systolic Arrays," in Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP, Vol. 9, pp. 778-781, March 1984. </li> | |||
<li> Machiraju Vijay and C. Siva Ram Murth, "Real-Time Simulations of Dynamic Systems on Systolic Arrays," in IEEE Transactions on Industrial Electronics, Vol. 45, No. 2, pp. 326-332, April 1998. </li> | |||
<li> Amber Roy-Chowdhury and Prithviraj Banerjee, "A Fault-Tolerant Parallel Algorithm for Iterative Solution of the Laplace Equation," in the International Conference on Parallel Processing, Vol. 3, pp. 133-140, Augus 1993. </li> | |||
<li> Yen-Tai Lai, Stephen S. T. Yau, and Ping-Hua Chen, "Design of The Ordinary Differential Equation Solver in The Yau Filterin System," in Proceedings of the 2002 American Control Conference, Vol. 6, pp. 5144-5149, May 2002. </li> | |||
<li> Susanta Sarkar, A. K. Majumdar "Fast Fourier transform using Linear Tagged Systolic Array" in IEEE Region 10 Conference on Computer and Communication Systems, Hong Kong, pp. 289-293, September 1990. </li> | |||
<li> [http://klabs.org/DEI/Processor/shuttle/shuttle_tech_conf/boykin_83.pdf "EVOLUTION OF SHUTTLE AVIONICS REDUNDANCY MANAGEMENT/FAULT TOLERANCE"] </li> | |||
<li>http://mpc.uci.edu/wget/www.tc.cornell.edu/Services/Edu/Topics/ParProgCons/ </li> | |||
</ol> | </ol> | ||
Latest revision as of 21:27, 4 February 2012
This article is a discussion on systolic arrays and their relation to MISD architectures. Since very little information and no examples are available on MISD, this article gives a brief introduction using Flynn's 1966 taxonomy on the subject. The article then presents a brief introduction to systolic arrays and discusses their mathematical uses and real-world engineering uses as examples. From these applications, the article shows where the claim that systolic arrays are examples of MISD is acceptable, and where it stretches the argued definition of MISD.
MISD
Micheal J. Flynn introduced the idea of an MISD (Multiple Instruction, Single Data) computer architectures in his original taxonomy in 1966.[1] The basic Flynn's architecture is as below
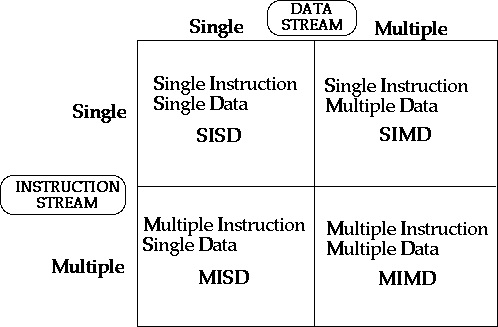
The MISD Architecture
Dr. Yan Solihin defines MISD as "..an architecture in which multiple processing elements execute from different instruction streams, and data is passed from one processing element to the next."[2] He also notes that MISD architectures are restricted to certain types of computations due to the requirement of data-passing between processing elements.[2] Each processing element executes different instructions on the data stream.[3] Every time the data is processed by a processing element, we can always argue that the data is no longer the original data introduced at the start of the stream.[4]
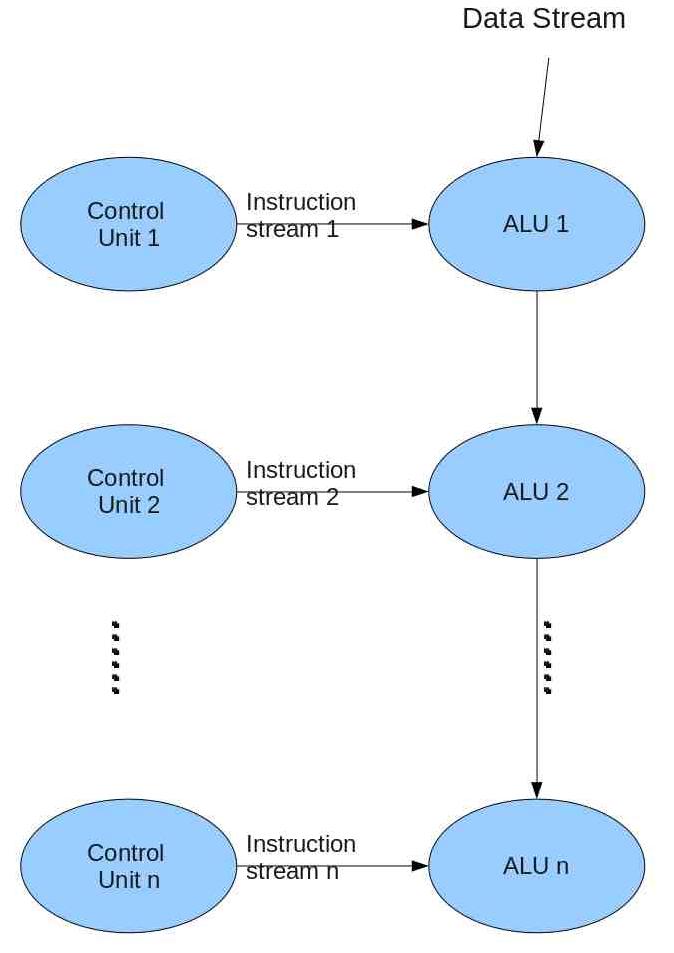
From this image, we see that the data stream has one clear entrance and exit into the system. What we are unsure of is if each processing element has access to a collective instruction storage or if all processing elements are embedded with an individual instruction storage. Depending on the specific system described, each processing element is generally function specific or predestined; but in some systems (similar to iWarp), each processing element may be quite advanced.
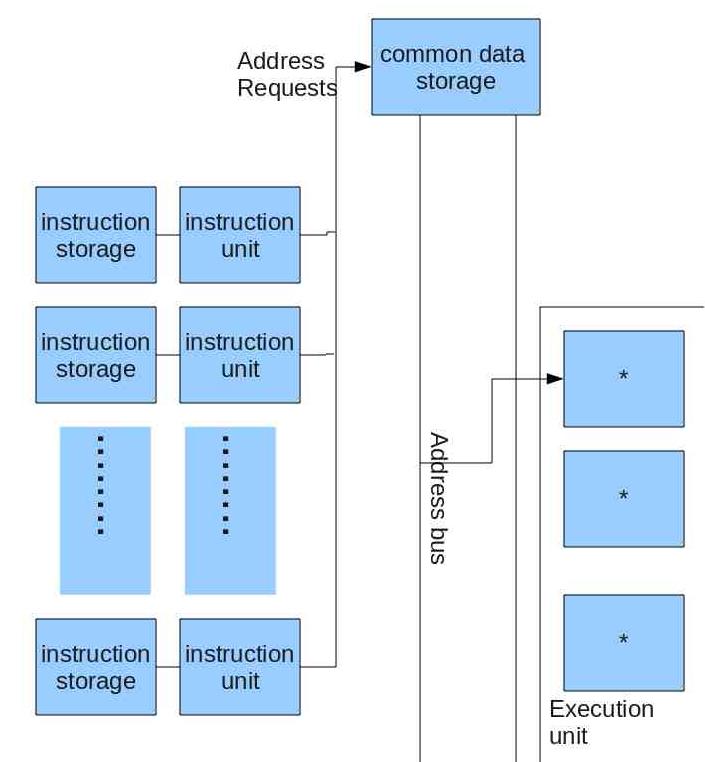
For this image, Flynn describes each processing element as an independent virtual machine that operates on independent program sequences. He explicitly states that each processing element has it's own private instruction memory, which limits the data stream as being the only interaction between instruction streams.[14]
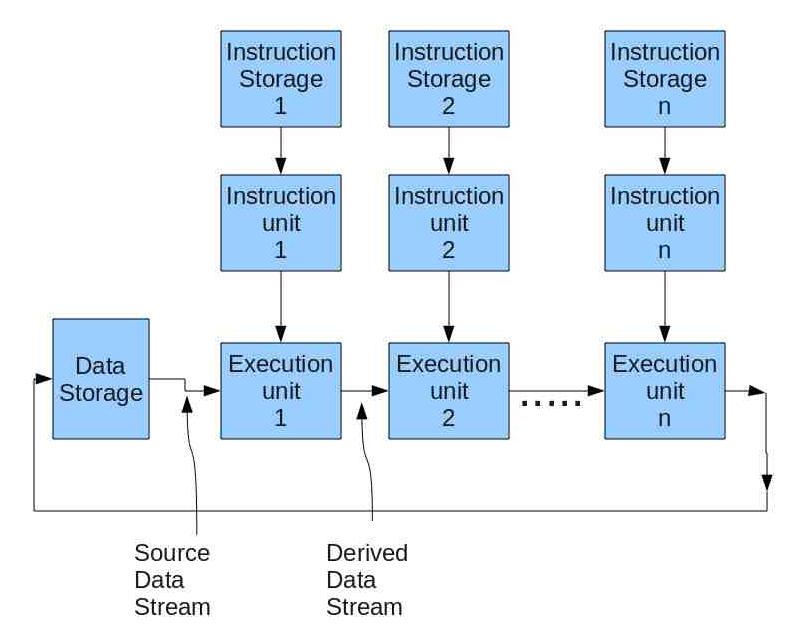
In this image, Flynn demonstrates a version of MISD in which the data stream is a force forwarding of operands between the execution units. An instruction that any individual execution unit sees can be fixed (flexible setup of units), semi-fixed (one pass of a data file), or variable (stream of instructions could operate on any point of the data stream)[14].
MISD Computers
While it is widely believed that no actual MISD computer exists in practice, it is controversially argued that a systolic array is the most common example of MISD[6]. One often cited example of MISD (most notable from the MISD wiki article) is the space shuttle flight-control computers. The authors of this article found no source material backing this claim (even the MISD wiki is awaiting a citation on the claim), and found very little on the actual architectures of those computers. The closest assumption for the claim the authors of this article could find is the system designed for redundancy management/fault tolerance[29], which [26] discusses the uses of systolic array in fault-tolerant systems.
Some arguments exist that pipelined vector processors could be considered an example of MISD architecture due to the fact that a different operation is performed on the data stream as it flows from stage to stage[6]. The argument against this idea is that individual processing elements in each stage do not technically fetch their operations from an instruction cache[6], but are more similar to a function specific, or ASIC, chip.
One application that exists for MISD VLSI architectures are applications which require multiple pattern matching in large data streams that lack any preprocessed indexes for lookups[8]. This research presents a set of recursive query semantics: "concatenation of basic strings and patterns, alphanumerical comparisons of simple strings, boolean operations on subexpressions, and hamming distance filtering"[12], and then explains that the recursion process of the semantics is best understood as a "..recursion tree where the result is found by propagating the results from the leaf nodes...to the root of the tree"[12].
Recently, Stanford University and Maxeler Technologies have been working on acceleration methodologies that benefit from combining different computer architectures. One of the proposed methodologies based on FPGA arrays uses SIMD for multiple data strips until the pin bandwidth limits the acceleration, then switches to an MISD-style pipeline of the FPGA arrays until acceleration is limited by circuit limitations[13]. Similar research on implementing MISD pipelines via FPGAs for biologicaly-inspired machine vision (VI-like) algorithms has been introduced in [18].
Systolic Array
The systolic array was first introduced in 1978 by Kung and Leiserson.[20]
What is a Systolic Array?
"A systolic array is an arrangement of processors in an array (often rectangular) where data flows synchronously across the array between neighbors"[7] Systolic arrays have data processing units (DPU) arranged in the form an matrix such that they are connected to their neighbors in the form of a mesh.[9]
The two models of systolic arrays are shown below:

The above diagram represents a systolic array where each DPU performs a specific operation on the data which can be input/output from an external source in the case of embedded systems or could be system generated by a auto sequencing memory unit. Each DPU performs a different computation based on the instruction set given to it and takes in data from the top or the left and then outputs it to it's right or below. A systolic array may or may not have local memory based on the application it is being used for.
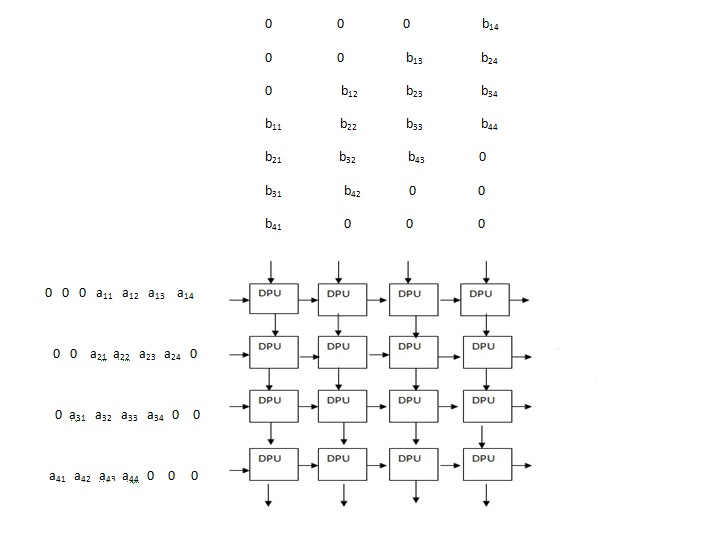
An example of an application of systolic array is a matrix multiplication. The systolic array can have a 4X4 mesh to multiply two 4X4 matrices where the data of all the rows and columns to be multiplied can be entered as the input into each DPU and the instruction executed by each DPU would be to multiply the incoming stream of numbers and add them to a previous value stored in it if there is any. The final output that is the resultant matrix would be the values stored in each DPU.
The function of each DPU in the above example is as follows 1)Each DPU takes as input a and b 2)Multiplies a ,b 3)It adds the value of multiplication to a previous value and stores the value of addition 4)Sends value of a to DPUij+1 if j is not 4 5)Sends value of b to DPUi+1j if i is not 4
Systolic arrays can be used to make algorithms involving a lot of parallel computation much easier. "Systolic array processors have been known to be extremely efficient at executing the class of algorithms that exhibit tight coupling between neighboring cells via data transfers in an N-dimensional model space."[11] Though the size of the array does affect the performance. Small systolic arrays present timing issues, limitations on bus width and chip pins, as well as pipeline drain caused by interruptions in the data flow. Approaches discussed to resolve these issues were problem partition (either the specified algorithm or the data array), array emulation (time-sharing a small array's processors to mimic a larger array more properly suited to the specified algorithm), and software based scheduling programs.[15] The size of a systolic array is primarily determined by the number of individual processing elements and the total computation time needed for the specific algorithm, but then this also depends on the length of the loop and the transformation matrix of the specific algorithm.[17]
Applications of Systolic Arrays
Various complex systems that can be optimized with systolic arrays include:
- Video Filtering
- Data Compression
- Image Processing
- Signal Processing
- Graphic Algorithms
- Biological Sequence Comparison
Systolic arrays are useful in these applications due to their usefulness in efficiently accelerating computation-intense problems ("..problems where the amount of computation required to solve the problem is very large compared to the amount of input/output"[25]) like vector-matrix multiplication, Discrete Fourier Transforms (DFT), Fast Fourier Transforms (FFT), convolution, Dynamic Time Warping (DTW), and differential equations. [26] also presents data supporting the use of systolic array for algorithm-based fault tolerant systems, using Laplace's equation as an example.
Discrete Fourier Transforms
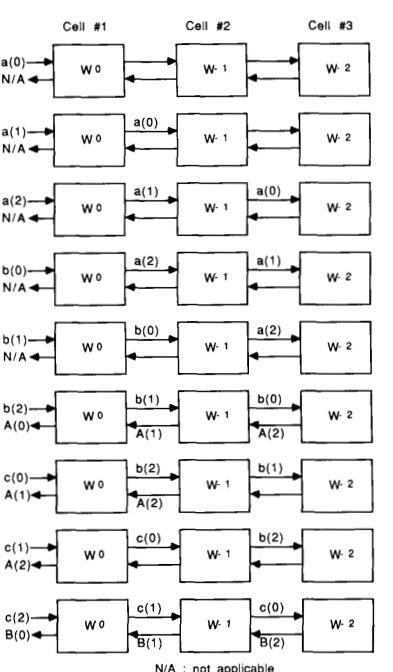
The advancement of VLSI systolic arrays became the first preference to use for the digital processing algorithms as systolic array's could solve complicated problems by just using array which are similar.A Discrete Fourier transform (DFT) could be efficiently calculated using a one dimensional systolic array which was formed by using a modification of First order Goertzel algorithm.
The picture on the right shows a systolic array for a 3 point DFT.The data is sent continuously into the array and a each cell takes in a sample to calculate one DFT sample.Each cell has an adder and PROM multiplier .After calculating one sample the cells send the data to their neighbors and hence a new sample is available at each cell again for computation.The input given is {a(0),a(1),a(2)} ,{b(0),b(1),b(2)}, {c(0),c(1),c(2)} and the output DFT vectors are {A(0),A(1),A(2)} , {B(0),B(1),B(2)} , {C(0),C(1),C(2)}.
"Each cell accumulates partial terms of one particular DFT sample" [19 ]
Fast Fourier transform
[28] uses a special type of systolic array called Tagged Systolic Array(TSA)to solve Fast Fourier Transform , as they cannot be represented in the form of uniform recurrence equations which makes the formulation of a simple systolic array to solve it difficult.
In a TSA "tags are attached to the results of a particular computation for properly routing them to other processing elements (PES)/DPU's where the result of that particular computation is required." [28] It uses the communication links of only the nearest neighbors to send its data.
To design a systolic array for an FFT the index points should be mapped to a smaller number of processing elements which should be connected. But the problem arises as the PE's which generate the variable and the PE which use the variable might not necessarily be neighbors in this case and also the location of destination PE might change with time and location of the source." In such cases tags (evaluated based on location and time) are attached to the data generated at the source PE for proper routing of data. This type of architecture that uses tags for data routing is called a Tagged Systolic Array (TSA)"
The TSA for FFT is a linear array and uses tags to pass data.
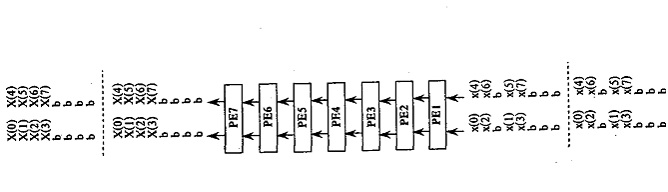
Each PE stores two kinds of data one for computation and the other is an intermediate result as well as two tags which are always constant. "The tag of a data is checked at a PE to determine its further direction of movement or to decide whether the data is required at the PE itself." If the data is required by the PE it stores it else it forwards it to its neighboring PE.
All the PE's in the pipeline are divided into various groups such that each group is used for calculating a different stage of a FFT. PE's in one group perform a similar operation. In the figure "PE1 performs the computations of stage 1, PE2 & PE3 perform computations of stage 2 and PE4, PE5,PE6 & PE7 are responsible for stage 3 computation."[28]
Convolution
In 2003, the idea of a super-systolic array was introduced by Jae-Jin Lee and Gi-Yong Son. [16] explains that a super-systolic array involves making cells of systolic array themselves a systolic array and defines the use of a super-systolic array for convolution as "..a logical systolic array in a sense that the array assumes all operation to complete in a unit delay to maintain rhythmic data flow." For the convolution problem in [16], each cell in the systolic array is capable of performing multiplication and addition. It is the multiplication process that benefits highly from systolization, and is implemented as a systolic array in itself. Converting the cells of systolic array into systolic array themselves results in higher degrees of concurrency and lower resource consumption[16].
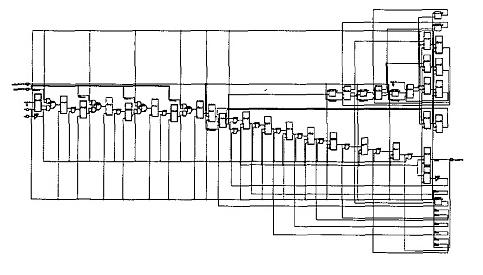
[22] introduces the concept of the moment-based systolic array of convolutions, which generally decreased to total delay associated with convolution implementations.
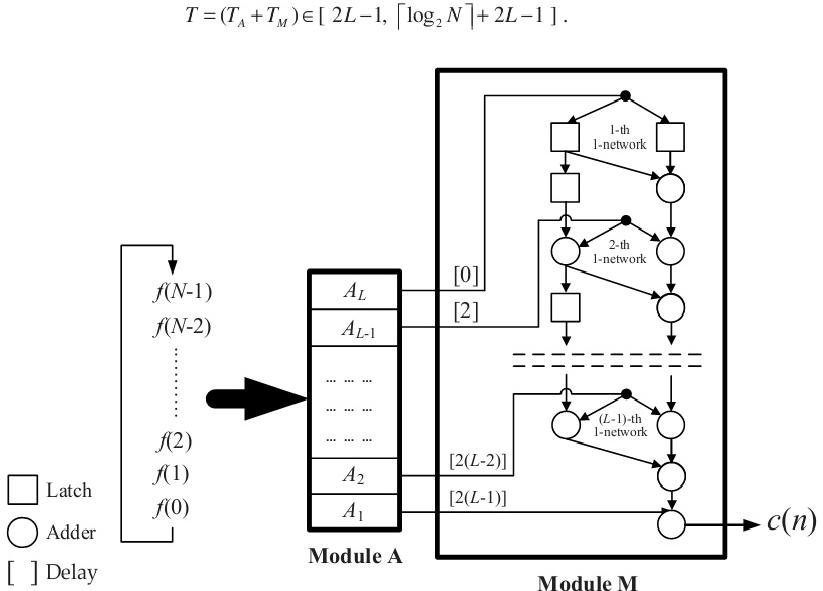
Dynamic Time Warping (DTW)
[24] introduces DTW as an array of identical processing units, each designed to compute local distance and global measurements of dissimilarity. Systolic arrays were discovered in [24] to reduce design costs and speed up processing time by processing a new reference pattern immediately following the completion of the previous reference pattern. [24] found that by precisely defining the kind of interconnections between each individual processing unit to suit particular application requirements bypassed the problem of only half the processing units working only half the time, thus they were able to obtain optimal performance for individual circuits and the system as a whole. Although, for [24], the individual processing units themselves are ASIC to the DTW algorithm being implemented.
Differential Equations (DEQ)
[25] discusses the use of systolic array for real-time simulations of industrial systems. They propose a system of three DEQs (N=3, four terms). The systolic array operates through each function, evaluating the four terms (simultaneously) and feeding the results back into itself. [25] explains that if the system is linear, the initial elements of the differential matrix are constant throughout the simulation; but if the system is nonlinear, new matrix elements are computed and loaded into the proper nodes of the systolic array. The proposed systolic array in [25] is seemingly re-configurable, in that as N changes, the array can adjust.
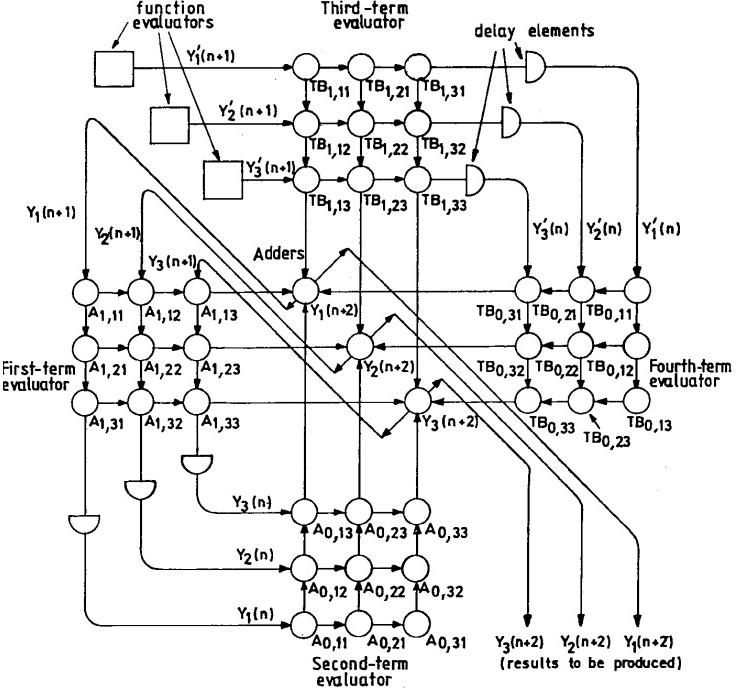
[27] discusses use of the Runge-Katta method to solve ordinary dynamic equations (ODE) and partial dynamic equations (PDE) within the Yau filtering system. The ability to perform parallel computations on systolic architectures became one advantage for using the Runge-Katta method. [27] is another example of the use of systolic array for matrix-vector multiplication, as well as vector addition.
Systolic Array vs. MISD
If relating to an MISD architecture, a systolic array is "..a network of small computing elements connected in a regular grid. All the elements are controlled by a global clock. On each cycle, an element will read a piece of data from one of its neighbors, perform a simple operation (e.g. add the incoming element to a stored value), and prepare a value to be written to a neighbor on the next step"[6]. This of course relates to the idea that typically the inner processing units (or nodes) of a systolic array do not access memory or buffers, but pass the data from node-to-node via registers. This relates to Flynn's taxonomy of MISD architecture correctly in that only the first and last processing units (nodes) will access the original data stream. Conversely, [21] describes a systolic array system quite unlike an MISD architecture by emphasizing that the systolic array pipeline reduces the need for control logic, control signal generation, and the cost of FSM design.
If a systolic array is not designed with a local memory, the individual processing units are then generally designed to be non-programmable (basically ASIC) and data is then introduced to the systolioc array through an outside shared memory controller (perhaps even through buffers to ease memory traffic)[15]. If designed without a local memory, then, a systolic array does not fit Flynn's taxonomy of MISD architecture: the data stream is still the only means of interaction between the individual processing units, but those individual processing units lack individual intruction memories. It could be argued to mimic SISD (single instruction, single data) at this point, since the processing units themself are generally application-specific. If a systolic array is designed with a local memory, it gains not only the ability to fetch data from that local memory[15], but also instructions. It could: a) have a local instruction memory, in which a program fetches and transmits instructions to each individual processing unit (on the assumption that each of those units is beyond application-specific), or b) attempt to mimic Flynn's MISD taxonomy and grant each of those individiaul processing units an individual instruction memory. The second option does present much overhead, and if not necessarily application or algorithm dependant, will be quite costly for no appearnt reason.
Consistently we see that one major design characteristic that either places a systolic array in the MISD list or forces it to stretch the definition is the idea of application-specification, or being problem specific. The MISD architecture Flynn describes are individual processing units that are typically the same as it's neighbors,[14] which we presume are guided by an ISA (instruction set architecture) capable of identification and execution of multiple operations. To achieve a systolic array that is more purely MISD, it must be re-configurable in some way. [17] defines a re-configurable systolic array as one "..that can be adapted to computing multiple problems through either software or hardware configuration, or both." [17] shows that one such way is to design the systolic array architecture such that two or more algorithms can mapped to a single re-configurable systolic array. This is done in two steps: compute individual algorithms one at a time with their proper control settings, then extend the array using time or space redundancy to compute multiple algorithms simultaneously. The space-time mapping procedure in [17] is achieved by mapping different algorithms to individual systolic arrays using one common transformation matrix, then extracting common parts of each circuit within processing units and merging those arrays into one re-configurable systolic array.
One final argument for the claim that calling systolic array an MISD architecture is stretching the definition of MISD is that generally, for most applications, both the data and instruction streams for systolic array are serial. This conflicts with Flynn's taxonomy of MISD because he classifies it as an example of parallel computer architecture[14] in which the instruction stream is parallel.
References
- Flynn, M. (1972). "Some Computer Organizations and Their Effectiveness". IEEE Trans. Comput. C-21: 948.
- Solihin, Y. (2008). "Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems". Solihin Publishing & Consulting LLC. C-1: 12.
- CSC 8383 Lecuture 5
- MISD wiki
- ECE506 Spring 2012 Lecture 1
- 3.1.3 MISD Computers
- Laiq hasan,Yahya M.Khawaja,Abdul Bais,"A Systolic Array Architecture for the Smith-Waterman Algorithm with High Performance Cell Design" in IADIS European Conference Data Mining, 2008, pp. 37
- Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, Vol. 12, No. 7, pp. 727, July 2004.
- Systolic array
- Systolic array architecture
- Robert E. Morley, Jr.Thomas J. Sullivan ,"A Massively Parallel Systolic Array Processor System," in Electronic Systems and Signals Research Laboratory,Department of Electrical Engineering,Washington University, pp. 217.
- Arne Halaas, Børge Svingen, Magnar Nedland, Pål Sætrom, Ola Snøve, Jr., Olaf René Birkelan, "A Recursive MISD Architecture for Pattern Matching," in IEEE Transactions on Very Large Scale Integration (VLSI) Systems, Vol. 12, No. 7, pp. 728, July 2004.
- Michael Flynn, R. Dimond, O. Mencer, O. Pell, "Finding Speedup in Parallel Processors," in International Symposium on Parallel and Distributed Computing, pp. 3, 2008.
- Michael J. Flnn, "Very High-Speed Computing Systems," Proceedings of the IEEE, Vol. 54, No. 12, pp.1908, December 1966.
- Henry Y. H. Chuang, Ling Chen, "A General Approach to Solving Arbitrarily Large Problems in a Fixed Size Systolic Array," in Proceedings of the Twenty-First Annual Hawaii International Conference on System Sciences, Vol. 2, Software Track, pp. 195-204, 1988.
- Jae-Jin Lee, Gi-Yong Song, "Implementation of the Super-Systolic Array for Convolution," in Proceedings of the ASP-DAC Asia and South Pacific Design Automation Conference, pp. 491-494, 2003.
- Wei Jin, Cang N. Zhang, and Hua Li, "Mapping Multiple Algorithms into a Reconfigurable Systolic Array," in Canadian Conference on Electrical and Computer Engineering, pp. 1187-1191, 2008.
- Vinay Sriram, David Cox, Kuen Hung Tsoi, and Wayne Luk, "Towards an Embedded Biologically-Inspired Machine Vision Processor," in International Conference on Field-Programmable Technology (FPT), pp. 273-278, 2010.
- J.A. Beraldin, Tyseer Aboulnasar, and Willem Steenart, "Efficient One-Dimensional Systolic Array Realization of the Discrete Fourier Transform," in IEEE Transactions of circuits and systems, Vol. 36, No. 1, pp. 95-100, January 1989.
- H. Kung, and C. Leiserson, “Systolic arrays (for VLSI),” in Sparse matrix proceedings, 1978. Society for Industrial & Appl. Mathematics, pp. 256–309, 1979.
- Liang Lu, Weiqiang Liu, Maire O’Neill, and Earl E. Swartzlander Jr., "QCA Systolic Array Design," in IEEE Transactions on Computers, Issue 99, December 2011.
- Jianguo Liu, Chao Pan, and Zhenbing Li, "Novel Convolutions using First-order Moments, in IEEE Transactions on Computers, Issue 99, July 2011.
- Matrix Multiplication using systolic array
- F. Jutand, N. Dennassieux, D. Vicard, and G Chollet, "VLSI Architectures For Dynamic Time Warping Using Systolic Arrays," in Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP, Vol. 9, pp. 778-781, March 1984.
- Machiraju Vijay and C. Siva Ram Murth, "Real-Time Simulations of Dynamic Systems on Systolic Arrays," in IEEE Transactions on Industrial Electronics, Vol. 45, No. 2, pp. 326-332, April 1998.
- Amber Roy-Chowdhury and Prithviraj Banerjee, "A Fault-Tolerant Parallel Algorithm for Iterative Solution of the Laplace Equation," in the International Conference on Parallel Processing, Vol. 3, pp. 133-140, Augus 1993.
- Yen-Tai Lai, Stephen S. T. Yau, and Ping-Hua Chen, "Design of The Ordinary Differential Equation Solver in The Yau Filterin System," in Proceedings of the 2002 American Control Conference, Vol. 6, pp. 5144-5149, May 2002.
- Susanta Sarkar, A. K. Majumdar "Fast Fourier transform using Linear Tagged Systolic Array" in IEEE Region 10 Conference on Computer and Communication Systems, Hong Kong, pp. 289-293, September 1990.
- "EVOLUTION OF SHUTTLE AVIONICS REDUNDANCY MANAGEMENT/FAULT TOLERANCE"
- http://mpc.uci.edu/wget/www.tc.cornell.edu/Services/Edu/Topics/ParProgCons/