CSC/ECE 506 Fall 2007/wiki2 4 md: Difference between revisions
| (2 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
Each processor is then assigned a different subset of ''s'' to evaluate. Once this is accomplished, an array ''D''[1:s,1:n+1] (where n = number of parameters) is created. Finally, the ''k'' sequences are used to initialize starting locations for each sequence using the first ''k'' elements in ''D'' such that Sk = D[k,1:n+1] (again where n = # of parameters). | Each processor is then assigned a different subset of ''s'' to evaluate. Once this is accomplished, an array ''D''[1:s,1:n+1] (where n = number of parameters) is created. Finally, the ''k'' sequences are used to initialize starting locations for each sequence using the first ''k'' elements in ''D'' such that Sk = D[k,1:n+1] (again where n = # of parameters). | ||
== Assignment == | == Assignment [http://en.wikipedia.org/wiki/Assignment_(computer_science)#Parallel_assignment] == | ||
Once the algorithm is completed and split into different parts, it is then partitioned into different complexes. The ''s'' points of ''D'' are partitioned into ''k'' different complexes {C1 ... Ck}. Each different complex contains ''m'' points. The first complex contains every k(j-1)+1 point of ''D'', the second contains k(j-1)+2 and so on (where j = 1,...m). | Once the algorithm is completed and split into different parts, it is then partitioned into different complexes. | ||
The ''s'' points of ''D'' are partitioned into ''k'' different complexes {C1 ... Ck}. Each different complex contains ''m'' points in each complex. While this is happening, all of the related data is kept together, so as to avoid confusion. The data is kept together through each array that it is stored in during the decomposition phase. During that phase arrays are created using matching data. The first complex contains every k(j-1)+1 point of ''D'', the second contains k(j-1)+2 and so on (where j = 1,...m). | |||
== Orchestration == | == Orchestration == | ||
Latest revision as of 02:30, 29 September 2007
Parallel Application: Shuffled Complex Evolution Metropolis
Overview
The scope of environmental sciences [1] increases significantly each year. With the advancement of computer systems, the advancements in measurement technologies, and a better understanding of environmental physics, more intricate (and thus realistic) environmental models are developed every year. With all of these factors to consider, it is no surprise that the number of parameters for computation increase each year as well.
The Department of Environmental Physics at Utrecht University [2] (specifically the writers of the paper this is based upon: Vrugt, Nuallain, Robinson, Bouten, Dekker and Sloot) thus propose the use of an algorithm, the Shuffled Complex Evolution Metropolis (SCEM-UA). The SCEM-UA algorithm is used for global optimization of the estimation of environmental models. With the amount of information and calculations needed to obtain a proper model, a parallel implementation of this algorithm is a great alternative. This algorithm, when implemented in a parallel structure, can be used for several model intricate case studies, such as the prediction of migratory bird flight paths.
Steps of Parallelization
Flow Chart Overview of Parallelization
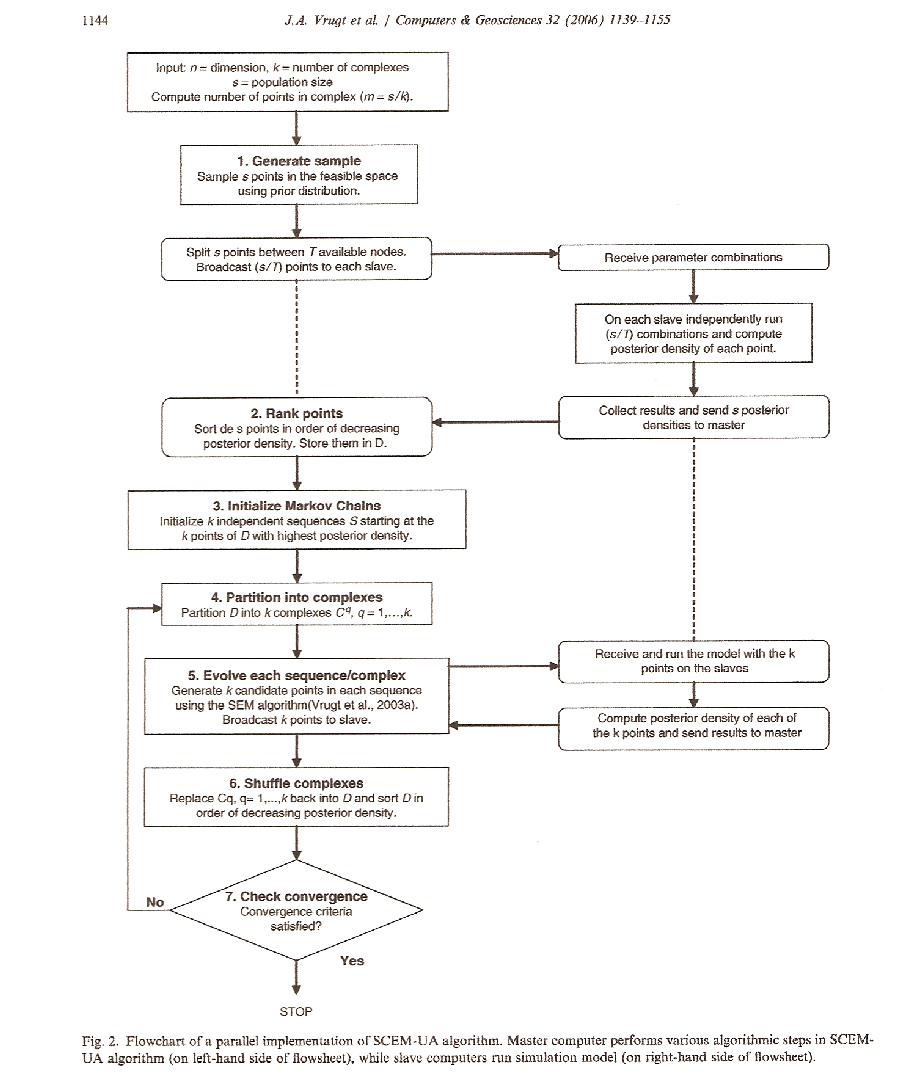
This flowchart illustrates the implementation of the SCEM-UA algorithm in a parallel scheme. A "master" computer (illustrated by the left side of the flowchart) perform the SCEM-UA algorithmic steps. A slave computer (illustrated by the right side of the flowchart) run the simulation model.
Decomposition
Decomposition in parallel processes is described as the division of the computation into various tasks. In the example of migratory birds, this task may be divided into different data sets such as population size, locations, etc. In the SCEM-UA algorithm, a dimension (n ), number of complexes (k ) and a population size (s ) are taken. The number of points, m, is then calculated using the formula:
m = s/k
Each processor is then assigned a different subset of s to evaluate. Once this is accomplished, an array D[1:s,1:n+1] (where n = number of parameters) is created. Finally, the k sequences are used to initialize starting locations for each sequence using the first k elements in D such that Sk = D[k,1:n+1] (again where n = # of parameters).
Assignment [3]
Once the algorithm is completed and split into different parts, it is then partitioned into different complexes.
The s points of D are partitioned into k different complexes {C1 ... Ck}. Each different complex contains m points in each complex. While this is happening, all of the related data is kept together, so as to avoid confusion. The data is kept together through each array that it is stored in during the decomposition phase. During that phase arrays are created using matching data. The first complex contains every k(j-1)+1 point of D, the second contains k(j-1)+2 and so on (where j = 1,...m).
Orchestration
The orchestration phase of parallelization is concerned with process communication and synchronization. Interestingly, this algorithm is not concerned with communication between processors, and in fact does not concern itself with communication among the processors! Because data sets are so large that the majority of computational time is alloted toward running the model code and/or generating the desired output.
Since data is stored into an array (referenced here as D ), once computations are complete, the array is sorted based upon decreasing posterior density.
Mapping
In the mapping of the SCEM-UA algorithm, it is vital that each processor has a different data set on which to work. Candidate points are generated and then sent to different nodes. Since each node is working on it's own set of data, and said data is stored into array D , there is no need for communication between processors (as described in "Orchestration").
References
Application of Parallel Computing to Stochastic Parameter Estimation in Environmental Models