CSC/ECE 506 Fall 2007/wiki2 3 pa: Difference between revisions
| (15 intermediate revisions by 2 users not shown) | |||
| Line 5: | Line 5: | ||
=='''LAMMPS Algorithm:''' == | =='''LAMMPS Algorithm:''' == | ||
The LAMMPS('''L'''arge Scale '''A'''tomic/'''M'''olecular '''M'''assively '''P'''arallel '''S'''ystem) algorithm is a classical [http://en.wikipedia.org/wiki/Molecular_dynamics molecular dynamics] code developed at [http://www.sandia.gov/index.html Sandia National Labs], New Mexico. This algorithm models the ensemble of particles in a solid, liquid or gaseous state. | The LAMMPS('''L'''arge Scale '''A'''tomic/'''M'''olecular '''M'''assively '''P'''arallel '''S'''ystem) algorithm is a classical [http://en.wikipedia.org/wiki/Molecular_dynamics molecular dynamics] code developed at [http://www.sandia.gov/index.html Sandia National Labs], New Mexico. This algorithm models the ensemble of particles in a solid, liquid or gaseous state.It can model atomic, polymeric, biological, metallic, or granular systems using a variety of force fields and boundary conditions and can be easily modified and extended. LAMMPS is distributed as an [http://lammps.sandia.gov/download.html open source code]. | ||
==='''Sequential Algorithm:'''=== | ==='''Sequential Algorithm:'''=== | ||
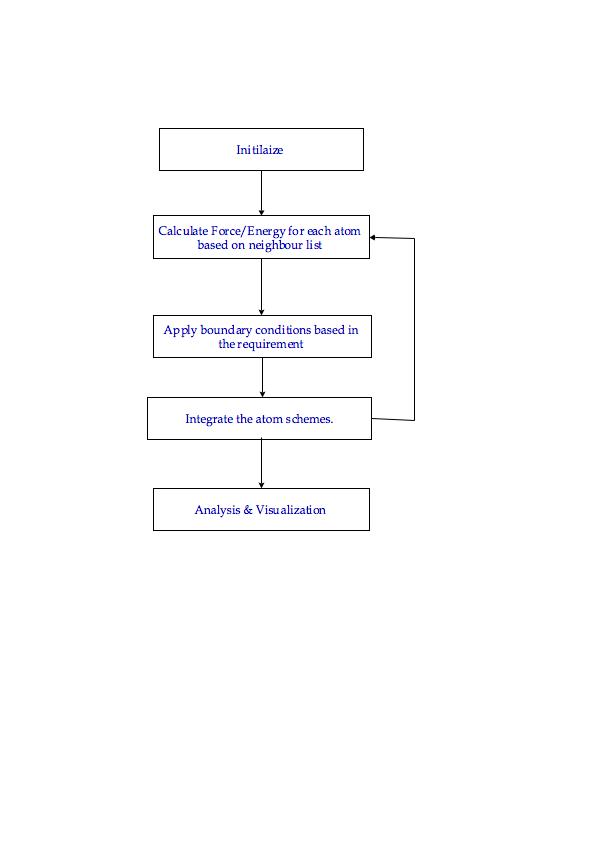
The initialization step sets up the various parameters for the atom like number of particles, initial velocity, temperature etc. This | This algorithm is performed for every atoms.The initialization step sets up the various parameters for the atom like number of particles, initial velocity, temperature etc. Once the initialization is completed the various required parameters are calculated(In this flow chart the force/energy is given as an example). After the parameters are calculated the necessary boundary conditions are applied & the atom schemes are integrated to get the desired results. This step is repeated for all the atom schemes. After the results for all the atom schemes are completed the results are analyzed & presented using visualizations schemes for further study. | ||
[[Image:Flow1.jpeg]] | [[Image:Flow1.jpeg]] | ||
| Line 16: | Line 16: | ||
The LAMMPS algorithm provides two levels of concurrency in a single time step just like the ocean problem. The function parallelism is performed across the grid where the parameters like the force, energy, temperature , pressure etc of the atom is computed. The data parallelism is performed for the function but with different data sets. | The LAMMPS algorithm provides two levels of concurrency in a single time step just like the ocean problem. The function parallelism is performed across the grid where the parameters like the force, energy, temperature , pressure etc of the atom is computed. The data parallelism is performed for the function but with different data sets. | ||
The LAMMPS algorithm decompose domain into a set of equal sized boxes. Since nearby atoms are placed on same processor, only neighboring atoms on different processor need to be communicated. The decomposition of the LAMMPS algorithm is spatial & the computation cost is of O(N/P) & the communication cost is of O(N/P). It should be noted that there is a possibility of load imbalance as the domain is decomposed into equal size boxes. | |||
==='''Orchestration''' === | ==='''Orchestration''' === | ||
For computational efficiency LAMMPS uses neighbor lists to keep track of the neighboring particles. The lists are optimized for systems with particles that are repulsive at short distances, so that the local density of particles never becomes too large. Communication is also minimized to optimal level by replicating force computations of boundary atoms. To increase computational efficiency the algorithm uses different timescales for different force computations. On parallel machines, LAMMPS uses spatial-decomposition techniques to partition the simulation domain into small three-dimensional sub-domains, one of which is assigned to each processor. | |||
The following snipit of code shows how the temperature is calculated for each sub-domain. A sub-domain is owned by a single processor and that constitutes a task. The temperature of the sub-domain is derived from the kinetic energy of each atom in the sub-domain. For each atom in the sub-domain, the square of the velocity in each dimension is accumulated, then multiplied by the mass of the atom. The final accumulated value of the sub-domain is sent to the root processor of the world using the MPI_Allreduce function. There, all the values are summed and a value is derived for the whole domain. | |||
double ComputeTemp::compute_scalar() | |||
{ | |||
double **v = atom->v; | |||
double *mass = atom->mass; | |||
double *rmass = atom->rmass; | |||
int *type = atom->type; | |||
int *mask = atom->mask; | |||
int nlocal = atom->nlocal; | |||
double t = 0.0; | |||
if (mass) { | |||
for (int i = 0; i < nlocal; i++) | |||
if (mask[i] & groupbit) | |||
t += (v[i][0]*v[i][0] + v[i][1]*v[i][1] + v[i][2]*v[i][2]) * | |||
mass[type[i]]; | |||
} else { | |||
for (int i = 0; i < nlocal; i++) | |||
if (mask[i] & groupbit) | |||
t += (v[i][0]*v[i][0] + v[i][1]*v[i][1] + v[i][2]*v[i][2]) * rmass[i]; | |||
} | |||
MPI_Allreduce(&t,&scalar,1,MPI_DOUBLE,MPI_SUM,world); | |||
if (dynamic) recount(); | |||
scalar *= tfactor; | |||
return scalar; | |||
} | |||
As for this snipit of code, it shows how the atoms in this sub-domain affect the atoms in the six neighboring sub-domains. The kinetic energy of each atom (affecting each neighbor) in this sub-domain are accumulated. The vector of values are sent to the root processor of the World. At the root, the vectors from all the sub-domain are accumulated and sent back to the sending processors. We can see that the MPI_Allreduce function was passed six items of a vector, which constitute six neighboring sub-domains. | |||
void ComputeTemp::compute_vector() | |||
{ | |||
int i; | |||
double **v = atom->v; | |||
double *mass = atom->mass; | |||
double *rmass = atom->rmass; | |||
int *type = atom->type; | |||
int *mask = atom->mask; | |||
int nlocal = atom->nlocal; | |||
double massone,t[6]; | |||
for (i = 0; i < 6; i++) t[i] = 0.0; | |||
for (i = 0; i < nlocal; i++) | |||
if (mask[i] & groupbit) { | |||
if (mass) massone = mass[type[i]]; | |||
else massone = rmass[i]; | |||
t[0] += massone * v[i][0]*v[i][0]; | |||
t[1] += massone * v[i][1]*v[i][1]; | |||
t[2] += massone * v[i][2]*v[i][2]; | |||
t[3] += massone * v[i][0]*v[i][1]; | |||
t[4] += massone * v[i][0]*v[i][2]; | |||
t[5] += massone * v[i][1]*v[i][2]; | |||
} | |||
MPI_Allreduce(t,vector,6,MPI_DOUBLE,MPI_SUM,world); | |||
for (i = 0; i < 6; i++) vector[i] *= force->mvv2e; | |||
} | |||
==='''Mapping''' === | ==='''Mapping''' === | ||
| Line 25: | Line 88: | ||
The LAMMPS suite utilizes the Message-Passing parallel computing model. This implies that each processor has a copy of all the data. It performs its operations and it sends, receives and broadcasts data as necessary. The LAMMPS suite defines a Universe where all the processors belong. The LAMMPS suite defines a number of Worlds in case different unrelated simulations should run. However, if all the processors available are used to tackle a single problem, then the Universe is said to contain one World. Each processor has its own copy of the LAMMPS suite and it knows some information about the Universe such as its processor ID, the number of processors in the Universe, the World it belongs to, the number of processors in its world and the total number of worlds. In each world, there exists a processor, which is called the Root processor. Also, the Message-Passing interface is defined for each processor to enable it to communicate with its six neighboring processors in its three-dimensional world. | The LAMMPS suite utilizes the Message-Passing parallel computing model. This implies that each processor has a copy of all the data. It performs its operations and it sends, receives and broadcasts data as necessary. The LAMMPS suite defines a Universe where all the processors belong. The LAMMPS suite defines a number of Worlds in case different unrelated simulations should run. However, if all the processors available are used to tackle a single problem, then the Universe is said to contain one World. Each processor has its own copy of the LAMMPS suite and it knows some information about the Universe such as its processor ID, the number of processors in the Universe, the World it belongs to, the number of processors in its world and the total number of worlds. In each world, there exists a processor, which is called the Root processor. Also, the Message-Passing interface is defined for each processor to enable it to communicate with its six neighboring processors in its three-dimensional world. | ||
'''References''' | |||
1: [http://lammps.sandia.gov/ LAMMPS website] | |||
2: [http://etd.lib.fsu.edu/theses/available/etd-07122004-165317/unrestricted/02_JK_RestThesis.pdf Sequential algorithm] | |||
Latest revision as of 14:55, 24 September 2007
Topic: Parallelizing an application
Pick another parallel application, not covered in the text, and less than 7 years old, and describe the various steps in parallelizing it (decomposition, assignment, orchestration, and mapping). You may use an example from the peer-reviewed literature, or a Web page. You do not have to go into great detail, but you should describe enough about these four stages to make the algorithm interesting.
LAMMPS Algorithm:
The LAMMPS(Large Scale Atomic/Molecular Massively Parallel System) algorithm is a classical molecular dynamics code developed at Sandia National Labs, New Mexico. This algorithm models the ensemble of particles in a solid, liquid or gaseous state.It can model atomic, polymeric, biological, metallic, or granular systems using a variety of force fields and boundary conditions and can be easily modified and extended. LAMMPS is distributed as an open source code.
Sequential Algorithm:
This algorithm is performed for every atoms.The initialization step sets up the various parameters for the atom like number of particles, initial velocity, temperature etc. Once the initialization is completed the various required parameters are calculated(In this flow chart the force/energy is given as an example). After the parameters are calculated the necessary boundary conditions are applied & the atom schemes are integrated to get the desired results. This step is repeated for all the atom schemes. After the results for all the atom schemes are completed the results are analyzed & presented using visualizations schemes for further study.
Decomposition & Assignment
The LAMMPS algorithm provides two levels of concurrency in a single time step just like the ocean problem. The function parallelism is performed across the grid where the parameters like the force, energy, temperature , pressure etc of the atom is computed. The data parallelism is performed for the function but with different data sets.
The LAMMPS algorithm decompose domain into a set of equal sized boxes. Since nearby atoms are placed on same processor, only neighboring atoms on different processor need to be communicated. The decomposition of the LAMMPS algorithm is spatial & the computation cost is of O(N/P) & the communication cost is of O(N/P). It should be noted that there is a possibility of load imbalance as the domain is decomposed into equal size boxes.
Orchestration
For computational efficiency LAMMPS uses neighbor lists to keep track of the neighboring particles. The lists are optimized for systems with particles that are repulsive at short distances, so that the local density of particles never becomes too large. Communication is also minimized to optimal level by replicating force computations of boundary atoms. To increase computational efficiency the algorithm uses different timescales for different force computations. On parallel machines, LAMMPS uses spatial-decomposition techniques to partition the simulation domain into small three-dimensional sub-domains, one of which is assigned to each processor.
The following snipit of code shows how the temperature is calculated for each sub-domain. A sub-domain is owned by a single processor and that constitutes a task. The temperature of the sub-domain is derived from the kinetic energy of each atom in the sub-domain. For each atom in the sub-domain, the square of the velocity in each dimension is accumulated, then multiplied by the mass of the atom. The final accumulated value of the sub-domain is sent to the root processor of the world using the MPI_Allreduce function. There, all the values are summed and a value is derived for the whole domain.
double ComputeTemp::compute_scalar()
{
double **v = atom->v;
double *mass = atom->mass;
double *rmass = atom->rmass;
int *type = atom->type;
int *mask = atom->mask;
int nlocal = atom->nlocal;
double t = 0.0;
if (mass) {
for (int i = 0; i < nlocal; i++)
if (mask[i] & groupbit)
t += (v[i][0]*v[i][0] + v[i][1]*v[i][1] + v[i][2]*v[i][2]) *
mass[type[i]];
} else {
for (int i = 0; i < nlocal; i++)
if (mask[i] & groupbit)
t += (v[i][0]*v[i][0] + v[i][1]*v[i][1] + v[i][2]*v[i][2]) * rmass[i];
}
MPI_Allreduce(&t,&scalar,1,MPI_DOUBLE,MPI_SUM,world); if (dynamic) recount(); scalar *= tfactor; return scalar; }
As for this snipit of code, it shows how the atoms in this sub-domain affect the atoms in the six neighboring sub-domains. The kinetic energy of each atom (affecting each neighbor) in this sub-domain are accumulated. The vector of values are sent to the root processor of the World. At the root, the vectors from all the sub-domain are accumulated and sent back to the sending processors. We can see that the MPI_Allreduce function was passed six items of a vector, which constitute six neighboring sub-domains.
void ComputeTemp::compute_vector()
{
int i;
double **v = atom->v; double *mass = atom->mass; double *rmass = atom->rmass; int *type = atom->type; int *mask = atom->mask; int nlocal = atom->nlocal;
double massone,t[6]; for (i = 0; i < 6; i++) t[i] = 0.0;
for (i = 0; i < nlocal; i++)
if (mask[i] & groupbit) {
if (mass) massone = mass[type[i]];
else massone = rmass[i];
t[0] += massone * v[i][0]*v[i][0];
t[1] += massone * v[i][1]*v[i][1];
t[2] += massone * v[i][2]*v[i][2];
t[3] += massone * v[i][0]*v[i][1];
t[4] += massone * v[i][0]*v[i][2];
t[5] += massone * v[i][1]*v[i][2];
}
MPI_Allreduce(t,vector,6,MPI_DOUBLE,MPI_SUM,world); for (i = 0; i < 6; i++) vector[i] *= force->mvv2e; }
Mapping
The LAMMPS suite utilizes the Message-Passing parallel computing model. This implies that each processor has a copy of all the data. It performs its operations and it sends, receives and broadcasts data as necessary. The LAMMPS suite defines a Universe where all the processors belong. The LAMMPS suite defines a number of Worlds in case different unrelated simulations should run. However, if all the processors available are used to tackle a single problem, then the Universe is said to contain one World. Each processor has its own copy of the LAMMPS suite and it knows some information about the Universe such as its processor ID, the number of processors in the Universe, the World it belongs to, the number of processors in its world and the total number of worlds. In each world, there exists a processor, which is called the Root processor. Also, the Message-Passing interface is defined for each processor to enable it to communicate with its six neighboring processors in its three-dimensional world.
References