CSC/ECE 506 Spring 2011/ch2 JR: Difference between revisions
No edit summary |
|||
| (62 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
=Supplement to Chapter 2: The Data Parallel Programming Model= | =Supplement to Chapter 2: The Data Parallel Programming Model= | ||
Chapter 2 of [[#References | Solihin (2008)]] covers the shared memory and message passing parallel programming models. However, it does not give an historical context for the development of parallel programming models. It also does not address other commonly recognized parallel programming models like the [[#Definitions | ''task parallel'']] model or the [[#Definitions | ''data parallel'']] model, which have been covered in other treatments like [[#References | Foster (1995)]] and [[#References | Culler (1999)]]. | |||
Shared memory and message passing models are often presented as competing models, but the data and task parallel models address fundamentally different programming concerns and can therefore be used in conjunction with either. The goal of this supplement is to provide historical context for the development of parallel programming models and a treatment of the data and task parallel models to complement Chapter 2 of [[#References | Solihin (2008)]]. | |||
= Overview = | |||
Whereas the shared memory and message passing models focus on how parallel tasks access common data, the [[#Definitions | ''data parallel'']] model focuses on how to divide up work into parallel tasks. Data parallel algorithms exploit parallelism by dividing a problem into a number of identical tasks which execute on different subsets of common data. The logical opposite of data parallel is task parallel, in which a number of distinct tasks operate on common data. Historically, each parallel programming model was developed to take advantage of advancements in computer architecture. | |||
= History = | = History = | ||
As computer architectures have evolved, so have parallel programming models. The earliest advancements in parallel computers took advantage of bit-level parallelism. These computers used vector processing, | As computer architectures have evolved, so have parallel programming models. The two factors that influenced parallel computing performance improvement the most were the speed of the individual processor and the speed of the communication connections. These communication connections include access to memory (local and main), as well as communication between processors. The earliest advancements in parallel computers took advantage of bit-level parallelism from improvements made to chip design. These computers mainly used vector processing and each processor had direct, fast conections to memory. This gave rise to the shared memory programming model. As performance returns from this architecture diminished and the complexity of building machines with direct access to memory increased, the emphasis was placed on instruction-level parallelism, distributed memory systems, and the message passing model began to dominate. Most recently, with the move to cluster-based machines, there has been an increased emphasis on thread-level parallelism. This has corresponded to an increase interest in the data-parallel programming model. | ||
== | == Shared memory in the 1970's == | ||
The major performance improvements from computers during this time were due to the ability to execute 32-bit word size operations at one time ([[#References|Culler (1999), p. 15.]]). The dominant supercomputers of the time, like the Cray and the ILLIAC IV, were mainly | The major performance improvements from computers during this time were due to the ability to execute 32-bit word size operations at one time ([[#References|Culler (1999), p. 15.]]). The dominant supercomputers of the time, like the Cray and the ILLIAC IV, were mainly [[#Definitions| ''SIMD'']] architectures and used a shared memory programming model. They each used different forms of vector processing ([[#References|Culler (1999), p. 21.]]). | ||
Development of the ILLIAC IV began in 1964 and wasn't finished until 1975 [http://en.wikipedia.org/wiki/ILLIAC_IV]. A central processor was connected to the main memory and delegated tasks to individual PE's, which each had their own memory cache. [http://archive.computerhistory.org/resources/text/Burroughs/Burroughs.ILLIAC%20IV.1974.102624911.pdf]. Each PE could operate either an 8-, 32- or 64-bit operand at a given time [http://archive.computerhistory.org/resources/text/Burroughs/Burroughs.ILLIAC%20IV.1974.102624911.pdf]. | Development of the ILLIAC IV began in 1964 and wasn't finished until 1975 [http://en.wikipedia.org/wiki/ILLIAC_IV]. A central processor was connected to the main memory and delegated tasks to individual PE's, which each had their own memory cache. [http://archive.computerhistory.org/resources/text/Burroughs/Burroughs.ILLIAC%20IV.1974.102624911.pdf]. Each PE could operate either an 8-, 32- or 64-bit operand at a given time [http://archive.computerhistory.org/resources/text/Burroughs/Burroughs.ILLIAC%20IV.1974.102624911.pdf]. | ||
The Cray machine was installed at Los Alamos National Laborartory in1976 by Control Data Corporation and had similar performance to the ILLIAC IV [http://en.wikipedia.org/wiki/ILLIAC_IV]. | The Cray machine was installed at Los Alamos National Laborartory in1976 by Cray Research, an offshoot of Control Data Corporation, and had similar performance to the ILLIAC IV [http://en.wikipedia.org/wiki/ILLIAC_IV]. For frequently-accessed data, the Cray machine relied heavily on the use of registers, instead of individual caches connected directly to processors like the ILLIAC IV. Each processor was connected to main memory and had a number of 64-bit registers used to perform operations [http://www.eecg.toronto.edu/~moshovos/ACA05/read/cray1.pdf]. | ||
All of these early commercial machines relied on there being a direct connection between each processor and the memory. Not only did there have to be a direct connection, but each connection had to allow relatively similar access to each part of memory. As you increased the number of processors, you had to increase the number of connections, which meant that this architecture did not scale well. At the same time, processors were becoming more and more advanced. The first single chip microprocessor was introduced in 1971 [http://en.wikipedia.org/wiki/Intel_4004]. Due to these two pressures, there was a movement away from large shared memory supercomputers and towards distributed memory systems. | |||
== Move to message passing in the 1980's == | |||
Increasing the word size above 32 bits offered diminishing returns in terms of performance ([[#References|Culler (1999), p. 15.]]), so there were fewer gains to be had for performance from processor improvements. At the same time, processors were becoming smaller and connections more efficient and connecting processors to do work in parallel became more viable. In the late 70's and early 80's Massively Parallel Processors (MPPs) emerged [http://www.intel.com/pressroom/kits/upcrc/parallelcomputing_backgrounder.pdf]. These consisted of separate computational units with their own memory and a link to the network that connects each unit. This structure allowed separate units to communicate the results of computations to each other without there needing to be a direct connection to each memory location. This change in architecture shifted the emphasis from bit-level parallelism to instruction-level parallelism, which involved increasing the number of instructions that could be executed at one time ([[#References|Culler (1999), p. 15.]]). The message-passing model allowed programmers the ability to divide up instructions in order to take advantage of this architecture. This gave rise to the message-passing model which allowed programmers the ability to divide up instructions in order to take advantage of this architecture. | |||
Organizing each of the nodes in a MPP posed its own problems. Some MPPs organized the connections into hypercubes, but these proved difficult to build [http://en.wikipedia.org/wiki/MIMD]. One of the most successful were the Connection Machines [http://ed-thelen.org/comp-hist/vs-cm-1-2-5.html]. Other architectures used 2-D meshes. All of these strategies meant that each message might have to pass through a number of nodes before reaching its final destination. This introduced its own restrictions on performance becaues each node had to handle routing duties. As networking technology became faster and faster, and individual processors became more and more efficient, it became reasonable to connect separate computers across a network, which gave rise to cluster machines. | |||
== Current trend to cluster machines == | |||
In the 1990's, off-the-shelf computers were becoming more and more powerful. At the same time, network connections were becoming faster and faster. These two trends meant that it was no longer necessary to build custom hardware for parallel computing, like the bit-serial processor machines. Off-the-shelf computers connected via networks could offer similar performance. These cluster-based machines added another layer of complexity to parallelism. Since computers could be located across a network from each other, there is more emphasis on software acting as a bridge [http://cobweb.ecn.purdue.edu/~pplinux/ppcluster.html]. This has led to a greater emphasis on thread- or task-level parallelism [http://en.wikipedia.org/wiki/Thread-level_parallelism] and the addition of the data parallelism programming model to existing message passing or shared memory models [http://en.wikipedia.org/wiki/Thread-level_parallelism]. | |||
= Data-Parallel Model = | |||
One important feature of the data-parallel programming model or data parallelism (SIMD) is the single control flow. Flynn's taxonomy classifies SIMD to be analogous to doing the same operation repeatedly over a large data set. There is only one control processor that directs the activities of all the processing elements. In a multiprocessor system executing a single set of instructions (SIMD), data parallelism is achieved when each processor performs the same task on different pieces of distributed data. In some situations, a single execution thread controls operations on all pieces of data. In others, different threads control the operation, but they execute the same code. | |||
== Description and example == | |||
This section shows a simple example adapted from Solihin textbook (pp. 24 - 27) that illustrates the data-parallel programming model. Each of the codes below are written in pseudo-code style. | |||
Suppose we want to perform the following task on an array <code>a</code>: updating each element of <code>a</code> by the product of itself and its index, and adding together the elements of <code>a</code> into the variable <code>sum</code>. The corresponding code is shown below. | |||
// simple sequential task | |||
sum = 0; | |||
'''for''' (i = 0; i < a.length; i++) | |||
{ | |||
a[i] = a[i] * i; | |||
sum = sum + a[i]; | |||
} | |||
When we orchestrate the task using the data-parallel programming model, the program can be divided into two parts. The first part performs the same operations on separate elements of the array for each processing element (sometimes referred to as PE or pe), and the second part reorganizes data among all processing elements (In our example data reorganization is summing up values across different processing elements). Since data-parallel programming model only defines the overall effects of parallel steps, the second part can be accomplished either through shared memory or message passing. The three code fragments below are examples for the first part of the program, shared-memory version of the second part, and message passing for the second part, respectively. | |||
// data parallel programming: let each PE perform the same task on different pieces of distributed data | |||
pe_id = getid(); | |||
my_sum = 0; | |||
'''for''' (i = pe_id; i < a.length; i += number_of_pe) //separate elements of the array are assigned to each PE | |||
{ | |||
a[i] = a[i] * i; | |||
my_sum = my_sum + a[i]; //all PEs accumulate elements assigned to them into local variable my_sum | |||
} | |||
In the above code, data parallelism is achieved by letting each processing element perform actions on array's separate elements, which are identified using the PE's id. For instance, if three processing elements are used then one processing element would start at i = 0, one would start at i = 1, and the last would start at i = 2. Since there are three processing elements then the index of the array for each will increase by three on each iteration until the task is complete (note that in our example elements assigned to each PE are interleaved instead of continuous). If the length of the array is a multiple of three then each processing element takes the same amount of time to execute its portion of the task. | |||
The picture below illustrates how elements of the array are assigned among different PEs for the specific case: length of the array is 7 and there are 3 PEs available. Elements in the array are marked by their indexes (0 to 6). As shown in the picture, PE0 will work on elements with index 0, 3, 6; PE1 is in charge of elements with index 1, 4; and elements with index 2, 5 are assigned to PE2. In this way, these 3 PEs work collectively on the array, while each PE works on different elements. Thus, data parallelism is achieved. | |||
[[Image:506wiki1.png|frame|center|150px|Illustration of data parallel programming(adapted from [http://computing.llnl.gov/tutorials/parallel_comp/#ModelsData Introduction to Parallel Computing])]] | |||
== Combining with message passing and shared memory == | |||
Although the shared-memory and message-passing models may be combined into hybrid approaches, the two models are fundamentally different ways of addressing the same problem (of access control to common data). In contrast, the data parallel model is concerned with a fundamentally different problem (how to divide work into parallel tasks). As such, the data parallel model may be used in conjunction with either the shared-memory or the message-passing model without conflict. In fact, Klaiber (1994) compares the performance of a number of data parallel programs implemented with both shared-memory and message-passing models. | |||
One of the major advantages of combining the data parallel and message-passing models is a reduction in the amount and complexity of communication required relative to a task parallel approach. Similarly, combining the data parallel and shared-memory models tends to simplify and reduce the amount of synchronization required. Much as the shared-memory model can benefit from specialized hardware, the data parallel programming model can as well. [[#Definitions |''SIMD'']] processors are specifically designed to run data parallel algorithms. These processors perform a single instruction on many different data locations simultaneously. Modern examples include CUDA processors developed by nVidia and Cell processors developed by STI (Sony, Toshiba, and IBM). For the curious, example code for CUDA processors is provided in the Appendix. However, whereas the shared-memory model can be a difficult and costly abstraction in the absence of hardware support, the data parallel model—like the message-passing model—does not require hardware support. | |||
= Task-Parallel Model = | |||
The logical opposite of data parallel is [[#Definitions | ''task parallel,'']] in which a number of distinct tasks operate on common data. Task parallelism is a form of parallelization where multiple instructions are executed either on same data or multiple data. It focuses on distributing execution of processes(threads) across different parallel computing nodes. As a part of workflow, different execution threads communicate with one another as they work to share data. | |||
== Description and example == | |||
An example of a task parallel code which is functionally equivalent to the sequential and data parallel codes given above follows below. | |||
// Task parallel code. | |||
int id = getmyid(); // assume id = 0 for thread 0, id = 1 for thread 1 | |||
if (id == 0) | |||
{ | |||
for (i = 0; i < 8; i++) | |||
{ | |||
a[i] = b[i] + c[i]; | |||
send_msg(P1, a[i]); | |||
} | |||
} | |||
else | |||
{ | |||
sum = 0; | |||
for (i = 0; i < 8; i++) | |||
{ | |||
recv_msg(P0, a[i]); | |||
if (a[i] > 0) | |||
sum = sum + a[i]; | |||
} | |||
Print sum; | |||
} | |||
In the code above, work is divided into two parallel tasks. The first performs the element-wise addition of arrays ''b'' and ''c'' and stores the result in ''a.'' The other sums the elements of ''a.'' These tasks both operate on all elements of ''a'' (rather than on separate chunks), and the code executed by each thread is different (rather than identical). | |||
The | |||
= Data Parallel Model = | = Data-Parallel Model vs. Task-Parallel Model = | ||
One important feature of data-parallel programming model or data parallelism (SIMD) is the single control flow: there is only one control processor that directs the activities of all the processing elements. In stark contrast to this is task parallelism (MIMD: Multiple Instruction, Multiple Data): characterized by its multiple control flows, it allows the concurrent execution of multiple instruction streams, each manipulates its own data and services separate functions. Below is a contrast between the data parallelism and task parallelism models from wikipedia: [http://en.wikipedia.org/wiki/SIMD SIMD] and [http://en.wikipedia.org/wiki/MIMD MIMD]. In the following subsections we continue to compare and contrast different features of data-parallel model and task-parallel model to help reader understand the unique characteristics of data-parallel programming model. | |||
[[Image:Smid.png|frame|center|425px|contrast between data parallelism and task parallelism]] | |||
Since each parallel task is unique, a major limitation of task parallel algorithms is that the maximum degree of parallelism attainable is limited to the number of tasks that have been formulated. This is in contrast to data parallel algorithms, which can be scaled easily to take advantage of an arbitrary number of processing elements. In addition, unique tasks are likely to have significantly different run times, making it more challenging to balance load across processors. [[#References | Haveraaen (2000)]] also notes that task parallel algorithms are inherently more complex, requiring a greater degree of communication and synchronization. | |||
== | == Synchronous vs asynchronous == | ||
While the [http://en.wikipedia.org/wiki/Lockstep_(computing) lockstep] imposed by data parallelism on all data streams ensures synchronous computation (all PEs perform their tasks at the exact same pace), every processor in task parallelism performs its task at their own pace, which we call asynchronous computation. Thus, at a certain point of a task parallel program's execution, communication and synchronization primitives are needed to allow different instruction streams to coordinate their efforts, and that is where variable-sharing and message-passing come into play. | |||
= | == Determinism vs. non-determinism == | ||
Data parallelism's synchronous nature and task parallelism's asynchronism give rise to another pair of features that add to the difference between these two models: determinism versus non-determinism. Data parallelism is deterministic, i.e. computing with the same input will always yield the same result, since its synchronism ensures that issues like relative timing between PEs will not arise. In contrast, task parallelism's asynchronous updates of common data can give rise to non-determinism, i.e, the same input won't always yield the same computation result (the result of a computation will depend also on factors outside the program control, such as scheduling and timing of other PEs). Obviously, non-determinism makes it harder to write and maintain correct programs. This partially explains the advantage of data parallel programming model over data parallelism in terms of development effort (also discussed in section 4.2). | |||
= Data Parallel | == Major differences between data parallel and task parallel models can broadly be classified as the following == | ||
{| class="wikitable" border="1" align="center" | |||
|+ '''Comparison between data parallel and task parallel programming models.''' | |||
|- | |||
! Aspects | |||
! Data Parallel | |||
! Task Parallel | |||
|- | |||
| Decomposition | |||
| Partition data into subsets | |||
| Partition program into subtasks | |||
|- | |||
| Parallel tasks | |||
| Identical | |||
| Unique | |||
|- | |||
| Degree of parallelism | |||
| Scales easily | |||
| Fixed | |||
|- | |||
| Load balancing | |||
| Easier | |||
| Harder | |||
|- | |||
| Communication overhead | |||
| Lower | |||
| Higher | |||
|} | |||
= Summary = | |||
As computer architectures have evolved, so have the parallel computing models. As discussed in [http://www.cesr.ncsu.edu/solihin Solihin], two models that have been prominent throughout computer history have been the shared-memory model and the message-passing model. These are, by no means, the only programming models in use. In this supplemental, we discussed two other important models: the task-parallel model and the data-parallel model. We also gave some context for how each of the programming models have emerged throughout the history of computer architecture. Each model has different strengths and weaknesses as discussed above. | |||
= Definitions = | = Definitions = | ||
* ''Data parallel.'' A data parallel algorithm is composed of a set of identical tasks which operate on different subsets of common data. | |||
* ''Task parallel.'' A task parallel algorithm is composed of a set of differing tasks which operate on common data. | |||
* ''SIMD (single-instruction-multiple-data).'' A processor which executes a single instruction simultaneously on multiple data locations. | |||
* '' MIMD (multiple-instruction-multiple-data).'' A processor architecture which can execute multiple instruction across multiple data elements simultaneously. | |||
= References = | = References = | ||
| Line 39: | Line 164: | ||
* Alexander C. Klaiber and Henry M. Levy, [http://portal.acm.org/citation.cfm?id=192020 "A comparison of message passing and shared memory architectures for data parallel programs,"] in ''Proceedings of the 21st Annual International Symposium on Computer Architecture,'' April 1994, pp. 94-105. | * Alexander C. Klaiber and Henry M. Levy, [http://portal.acm.org/citation.cfm?id=192020 "A comparison of message passing and shared memory architectures for data parallel programs,"] in ''Proceedings of the 21st Annual International Symposium on Computer Architecture,'' April 1994, pp. 94-105. | ||
* Yan Solihin, ''Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems,'' Solihin Books, 2008. | * Yan Solihin, ''Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems,'' Solihin Books, 2008. | ||
* Philip J. Hatcher, Michael Jay Quinn, ''Data-Parallel Programming on MIMD Computers'', The MIT Press, 1991. | |||
* Blaise Barney, "Introduction to Parallel Computing: Data Parallel Model", Lawrence Livermore National Laboratory, [https://computing.llnl.gov/tutorials/parallel_comp/#ModelsData https://computing.llnl.gov/tutorials/parallel_comp/#ModelsData], January 2009. | |||
* Guy Blelloch, "Is Parallel Programming Hard?", Carnegie Mellon University, [http://www.cilk.com/multicore-blog/bid/9108/Is-Parallel-Programming-Hard http://www.cilk.com/multicore-blog/bid/9108/Is-Parallel-Programming-Hard], April 2009. | |||
* Björn Lisper, ''Data parallelism and functional programming'', Lecture Notes in Computer Science, Volume 1132/1996, pp. 220-251, Springer Berlin, 1996. | |||
* ''SIMD'', Wikipedia, the free encyclopedia, [http://en.wikipedia.org/wiki/SIMD http://en.wikipedia.org/wiki/SIMD]. | |||
* ''MIMD'', Wikipedia, the free encyclopedia, [http://en.wikipedia.org/wiki/MIMD http://en.wikipedia.org/wiki/MIMD]. | |||
* ''Lockstep'', Wikipedia, the free encyclopedia, [http://en.wikipedia.org/wiki/Lockstep_(computing) http://en.wikipedia.org/wiki/Lockstep_(computing)]. | |||
* ''SPMD'', Wikipedia, the free encyclopedia, [http://en.wikipedia.org/wiki/SPMD http://en.wikipedia.org/wiki/SPMD]. | |||
Latest revision as of 04:44, 18 April 2011
Supplement to Chapter 2: The Data Parallel Programming Model
Chapter 2 of Solihin (2008) covers the shared memory and message passing parallel programming models. However, it does not give an historical context for the development of parallel programming models. It also does not address other commonly recognized parallel programming models like the task parallel model or the data parallel model, which have been covered in other treatments like Foster (1995) and Culler (1999).
Shared memory and message passing models are often presented as competing models, but the data and task parallel models address fundamentally different programming concerns and can therefore be used in conjunction with either. The goal of this supplement is to provide historical context for the development of parallel programming models and a treatment of the data and task parallel models to complement Chapter 2 of Solihin (2008).
Overview
Whereas the shared memory and message passing models focus on how parallel tasks access common data, the data parallel model focuses on how to divide up work into parallel tasks. Data parallel algorithms exploit parallelism by dividing a problem into a number of identical tasks which execute on different subsets of common data. The logical opposite of data parallel is task parallel, in which a number of distinct tasks operate on common data. Historically, each parallel programming model was developed to take advantage of advancements in computer architecture.
History
As computer architectures have evolved, so have parallel programming models. The two factors that influenced parallel computing performance improvement the most were the speed of the individual processor and the speed of the communication connections. These communication connections include access to memory (local and main), as well as communication between processors. The earliest advancements in parallel computers took advantage of bit-level parallelism from improvements made to chip design. These computers mainly used vector processing and each processor had direct, fast conections to memory. This gave rise to the shared memory programming model. As performance returns from this architecture diminished and the complexity of building machines with direct access to memory increased, the emphasis was placed on instruction-level parallelism, distributed memory systems, and the message passing model began to dominate. Most recently, with the move to cluster-based machines, there has been an increased emphasis on thread-level parallelism. This has corresponded to an increase interest in the data-parallel programming model.
The major performance improvements from computers during this time were due to the ability to execute 32-bit word size operations at one time (Culler (1999), p. 15.). The dominant supercomputers of the time, like the Cray and the ILLIAC IV, were mainly SIMD architectures and used a shared memory programming model. They each used different forms of vector processing (Culler (1999), p. 21.). Development of the ILLIAC IV began in 1964 and wasn't finished until 1975 [1]. A central processor was connected to the main memory and delegated tasks to individual PE's, which each had their own memory cache. [2]. Each PE could operate either an 8-, 32- or 64-bit operand at a given time [3].
The Cray machine was installed at Los Alamos National Laborartory in1976 by Cray Research, an offshoot of Control Data Corporation, and had similar performance to the ILLIAC IV [4]. For frequently-accessed data, the Cray machine relied heavily on the use of registers, instead of individual caches connected directly to processors like the ILLIAC IV. Each processor was connected to main memory and had a number of 64-bit registers used to perform operations [5].
All of these early commercial machines relied on there being a direct connection between each processor and the memory. Not only did there have to be a direct connection, but each connection had to allow relatively similar access to each part of memory. As you increased the number of processors, you had to increase the number of connections, which meant that this architecture did not scale well. At the same time, processors were becoming more and more advanced. The first single chip microprocessor was introduced in 1971 [6]. Due to these two pressures, there was a movement away from large shared memory supercomputers and towards distributed memory systems.
Move to message passing in the 1980's
Increasing the word size above 32 bits offered diminishing returns in terms of performance (Culler (1999), p. 15.), so there were fewer gains to be had for performance from processor improvements. At the same time, processors were becoming smaller and connections more efficient and connecting processors to do work in parallel became more viable. In the late 70's and early 80's Massively Parallel Processors (MPPs) emerged [7]. These consisted of separate computational units with their own memory and a link to the network that connects each unit. This structure allowed separate units to communicate the results of computations to each other without there needing to be a direct connection to each memory location. This change in architecture shifted the emphasis from bit-level parallelism to instruction-level parallelism, which involved increasing the number of instructions that could be executed at one time (Culler (1999), p. 15.). The message-passing model allowed programmers the ability to divide up instructions in order to take advantage of this architecture. This gave rise to the message-passing model which allowed programmers the ability to divide up instructions in order to take advantage of this architecture.
Organizing each of the nodes in a MPP posed its own problems. Some MPPs organized the connections into hypercubes, but these proved difficult to build [8]. One of the most successful were the Connection Machines [9]. Other architectures used 2-D meshes. All of these strategies meant that each message might have to pass through a number of nodes before reaching its final destination. This introduced its own restrictions on performance becaues each node had to handle routing duties. As networking technology became faster and faster, and individual processors became more and more efficient, it became reasonable to connect separate computers across a network, which gave rise to cluster machines.
Current trend to cluster machines
In the 1990's, off-the-shelf computers were becoming more and more powerful. At the same time, network connections were becoming faster and faster. These two trends meant that it was no longer necessary to build custom hardware for parallel computing, like the bit-serial processor machines. Off-the-shelf computers connected via networks could offer similar performance. These cluster-based machines added another layer of complexity to parallelism. Since computers could be located across a network from each other, there is more emphasis on software acting as a bridge [10]. This has led to a greater emphasis on thread- or task-level parallelism [11] and the addition of the data parallelism programming model to existing message passing or shared memory models [12].
Data-Parallel Model
One important feature of the data-parallel programming model or data parallelism (SIMD) is the single control flow. Flynn's taxonomy classifies SIMD to be analogous to doing the same operation repeatedly over a large data set. There is only one control processor that directs the activities of all the processing elements. In a multiprocessor system executing a single set of instructions (SIMD), data parallelism is achieved when each processor performs the same task on different pieces of distributed data. In some situations, a single execution thread controls operations on all pieces of data. In others, different threads control the operation, but they execute the same code.
Description and example
This section shows a simple example adapted from Solihin textbook (pp. 24 - 27) that illustrates the data-parallel programming model. Each of the codes below are written in pseudo-code style.
Suppose we want to perform the following task on an array a: updating each element of a by the product of itself and its index, and adding together the elements of a into the variable sum. The corresponding code is shown below.
// simple sequential task
sum = 0;
for (i = 0; i < a.length; i++)
{
a[i] = a[i] * i;
sum = sum + a[i];
}
When we orchestrate the task using the data-parallel programming model, the program can be divided into two parts. The first part performs the same operations on separate elements of the array for each processing element (sometimes referred to as PE or pe), and the second part reorganizes data among all processing elements (In our example data reorganization is summing up values across different processing elements). Since data-parallel programming model only defines the overall effects of parallel steps, the second part can be accomplished either through shared memory or message passing. The three code fragments below are examples for the first part of the program, shared-memory version of the second part, and message passing for the second part, respectively.
// data parallel programming: let each PE perform the same task on different pieces of distributed data
pe_id = getid();
my_sum = 0;
for (i = pe_id; i < a.length; i += number_of_pe) //separate elements of the array are assigned to each PE
{
a[i] = a[i] * i;
my_sum = my_sum + a[i]; //all PEs accumulate elements assigned to them into local variable my_sum
}
In the above code, data parallelism is achieved by letting each processing element perform actions on array's separate elements, which are identified using the PE's id. For instance, if three processing elements are used then one processing element would start at i = 0, one would start at i = 1, and the last would start at i = 2. Since there are three processing elements then the index of the array for each will increase by three on each iteration until the task is complete (note that in our example elements assigned to each PE are interleaved instead of continuous). If the length of the array is a multiple of three then each processing element takes the same amount of time to execute its portion of the task.
The picture below illustrates how elements of the array are assigned among different PEs for the specific case: length of the array is 7 and there are 3 PEs available. Elements in the array are marked by their indexes (0 to 6). As shown in the picture, PE0 will work on elements with index 0, 3, 6; PE1 is in charge of elements with index 1, 4; and elements with index 2, 5 are assigned to PE2. In this way, these 3 PEs work collectively on the array, while each PE works on different elements. Thus, data parallelism is achieved.
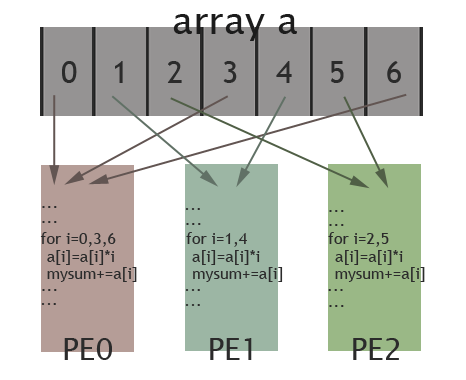
Although the shared-memory and message-passing models may be combined into hybrid approaches, the two models are fundamentally different ways of addressing the same problem (of access control to common data). In contrast, the data parallel model is concerned with a fundamentally different problem (how to divide work into parallel tasks). As such, the data parallel model may be used in conjunction with either the shared-memory or the message-passing model without conflict. In fact, Klaiber (1994) compares the performance of a number of data parallel programs implemented with both shared-memory and message-passing models.
One of the major advantages of combining the data parallel and message-passing models is a reduction in the amount and complexity of communication required relative to a task parallel approach. Similarly, combining the data parallel and shared-memory models tends to simplify and reduce the amount of synchronization required. Much as the shared-memory model can benefit from specialized hardware, the data parallel programming model can as well. SIMD processors are specifically designed to run data parallel algorithms. These processors perform a single instruction on many different data locations simultaneously. Modern examples include CUDA processors developed by nVidia and Cell processors developed by STI (Sony, Toshiba, and IBM). For the curious, example code for CUDA processors is provided in the Appendix. However, whereas the shared-memory model can be a difficult and costly abstraction in the absence of hardware support, the data parallel model—like the message-passing model—does not require hardware support.
Task-Parallel Model
The logical opposite of data parallel is task parallel, in which a number of distinct tasks operate on common data. Task parallelism is a form of parallelization where multiple instructions are executed either on same data or multiple data. It focuses on distributing execution of processes(threads) across different parallel computing nodes. As a part of workflow, different execution threads communicate with one another as they work to share data.
Description and example
An example of a task parallel code which is functionally equivalent to the sequential and data parallel codes given above follows below.
// Task parallel code.
int id = getmyid(); // assume id = 0 for thread 0, id = 1 for thread 1
if (id == 0)
{
for (i = 0; i < 8; i++)
{
a[i] = b[i] + c[i];
send_msg(P1, a[i]);
}
}
else
{
sum = 0;
for (i = 0; i < 8; i++)
{
recv_msg(P0, a[i]);
if (a[i] > 0)
sum = sum + a[i];
}
Print sum;
}
In the code above, work is divided into two parallel tasks. The first performs the element-wise addition of arrays b and c and stores the result in a. The other sums the elements of a. These tasks both operate on all elements of a (rather than on separate chunks), and the code executed by each thread is different (rather than identical).
Data-Parallel Model vs. Task-Parallel Model
One important feature of data-parallel programming model or data parallelism (SIMD) is the single control flow: there is only one control processor that directs the activities of all the processing elements. In stark contrast to this is task parallelism (MIMD: Multiple Instruction, Multiple Data): characterized by its multiple control flows, it allows the concurrent execution of multiple instruction streams, each manipulates its own data and services separate functions. Below is a contrast between the data parallelism and task parallelism models from wikipedia: SIMD and MIMD. In the following subsections we continue to compare and contrast different features of data-parallel model and task-parallel model to help reader understand the unique characteristics of data-parallel programming model.
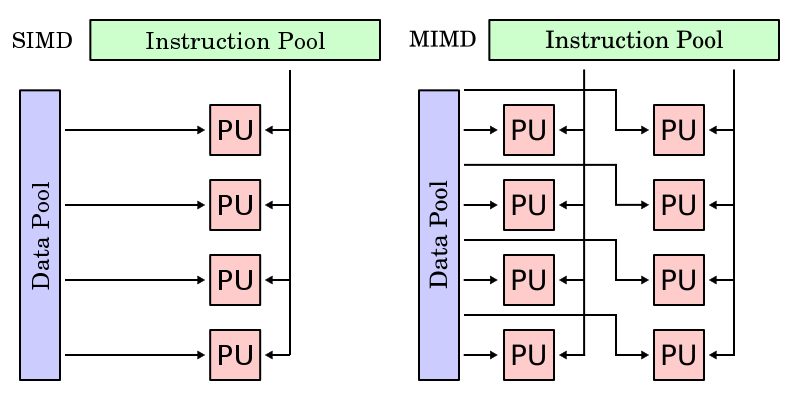
Since each parallel task is unique, a major limitation of task parallel algorithms is that the maximum degree of parallelism attainable is limited to the number of tasks that have been formulated. This is in contrast to data parallel algorithms, which can be scaled easily to take advantage of an arbitrary number of processing elements. In addition, unique tasks are likely to have significantly different run times, making it more challenging to balance load across processors. Haveraaen (2000) also notes that task parallel algorithms are inherently more complex, requiring a greater degree of communication and synchronization.
Synchronous vs asynchronous
While the lockstep imposed by data parallelism on all data streams ensures synchronous computation (all PEs perform their tasks at the exact same pace), every processor in task parallelism performs its task at their own pace, which we call asynchronous computation. Thus, at a certain point of a task parallel program's execution, communication and synchronization primitives are needed to allow different instruction streams to coordinate their efforts, and that is where variable-sharing and message-passing come into play.
Determinism vs. non-determinism
Data parallelism's synchronous nature and task parallelism's asynchronism give rise to another pair of features that add to the difference between these two models: determinism versus non-determinism. Data parallelism is deterministic, i.e. computing with the same input will always yield the same result, since its synchronism ensures that issues like relative timing between PEs will not arise. In contrast, task parallelism's asynchronous updates of common data can give rise to non-determinism, i.e, the same input won't always yield the same computation result (the result of a computation will depend also on factors outside the program control, such as scheduling and timing of other PEs). Obviously, non-determinism makes it harder to write and maintain correct programs. This partially explains the advantage of data parallel programming model over data parallelism in terms of development effort (also discussed in section 4.2).
Major differences between data parallel and task parallel models can broadly be classified as the following
| Aspects | Data Parallel | Task Parallel |
|---|---|---|
| Decomposition | Partition data into subsets | Partition program into subtasks |
| Parallel tasks | Identical | Unique |
| Degree of parallelism | Scales easily | Fixed |
| Load balancing | Easier | Harder |
| Communication overhead | Lower | Higher |
Summary
As computer architectures have evolved, so have the parallel computing models. As discussed in Solihin, two models that have been prominent throughout computer history have been the shared-memory model and the message-passing model. These are, by no means, the only programming models in use. In this supplemental, we discussed two other important models: the task-parallel model and the data-parallel model. We also gave some context for how each of the programming models have emerged throughout the history of computer architecture. Each model has different strengths and weaknesses as discussed above.
Definitions
- Data parallel. A data parallel algorithm is composed of a set of identical tasks which operate on different subsets of common data.
- Task parallel. A task parallel algorithm is composed of a set of differing tasks which operate on common data.
- SIMD (single-instruction-multiple-data). A processor which executes a single instruction simultaneously on multiple data locations.
- MIMD (multiple-instruction-multiple-data). A processor architecture which can execute multiple instruction across multiple data elements simultaneously.
References
- David E. Culler, Jaswinder Pal Singh, and Anoop Gupta, Parallel Computer Architecture: A Hardware/Software Approach, Morgan-Kauffman, 1999.
- Ian Foster, Designing and Building Parallel Programs, Addison-Wesley, 1995.
- Magne Haveraaen, "Machine and collection abstractions for user-implemented data-parallel programming," Scientific Programming, 8(4):231-246, 2000.
- W. Daniel Hillis and Guy L. Steele, Jr., "Data parallel algorithms," Communications of the ACM, 29(12):1170-1183, December 1986.
- Alexander C. Klaiber and Henry M. Levy, "A comparison of message passing and shared memory architectures for data parallel programs," in Proceedings of the 21st Annual International Symposium on Computer Architecture, April 1994, pp. 94-105.
- Yan Solihin, Fundamentals of Parallel Computer Architecture: Multichip and Multicore Systems, Solihin Books, 2008.
- Philip J. Hatcher, Michael Jay Quinn, Data-Parallel Programming on MIMD Computers, The MIT Press, 1991.
- Blaise Barney, "Introduction to Parallel Computing: Data Parallel Model", Lawrence Livermore National Laboratory, https://computing.llnl.gov/tutorials/parallel_comp/#ModelsData, January 2009.
- Guy Blelloch, "Is Parallel Programming Hard?", Carnegie Mellon University, http://www.cilk.com/multicore-blog/bid/9108/Is-Parallel-Programming-Hard, April 2009.
- Björn Lisper, Data parallelism and functional programming, Lecture Notes in Computer Science, Volume 1132/1996, pp. 220-251, Springer Berlin, 1996.
- SIMD, Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/SIMD.
- MIMD, Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/MIMD.
- Lockstep, Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/Lockstep_(computing).
- SPMD, Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/SPMD.