CSC/ECE 506 Spring 2011/ch4a ob: Difference between revisions
| (69 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
=Introduction= | =Introduction= | ||
The Nelder Mead Algorithm | The [http://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method Nelder-Mead Algorithm] is a [http://en.wikipedia.org/wiki/Simplex simplex] method for function minimization developed by J. A. Nelder and R. Mead in 1965<sup><span id="2body">[[#2foot|[2]]]</span></sup>. The method is used for minimizing an <tt>N</tt> dimensional function, by comparing the function values at <tt>n+1</tt> vertices of a [http://en.wikipedia.org/wiki/Simplex simplex], followed by the replacement of the vertex with highest function value by another vertex having a lower function value. The algorithm, by itself is highly serial in nature. | ||
= Serial Nelder Mead Function Minimization Algorithm (Serial Simplex Method)= | In this article, we will discuss the Serial Nelder-Mead Algorithm and its parallelization at Algorithmic level and Task Level. For the Algorithmic level parallelism, we will look at a method to replace more than one point from the simplex in a single iteration. For task level parallelism, we will pick individual tasks from the algorithm and try to parallelize them using methods like data parallel programming, shared memory programming and message passing. The choice of methods for task level parallelism largely depends on the underlying hardware and the computation / communication overhead for each of the methods. | ||
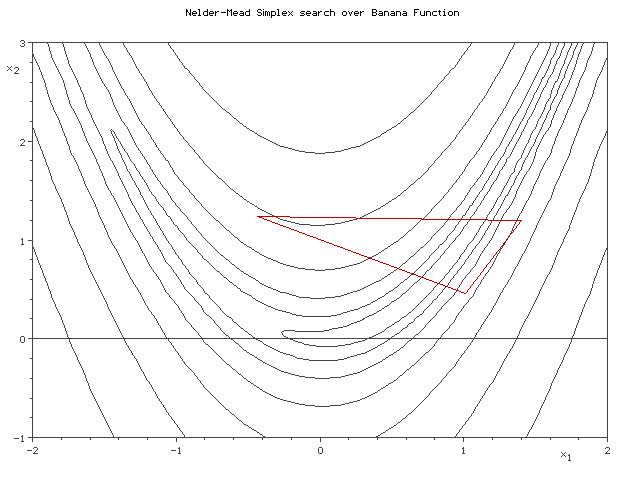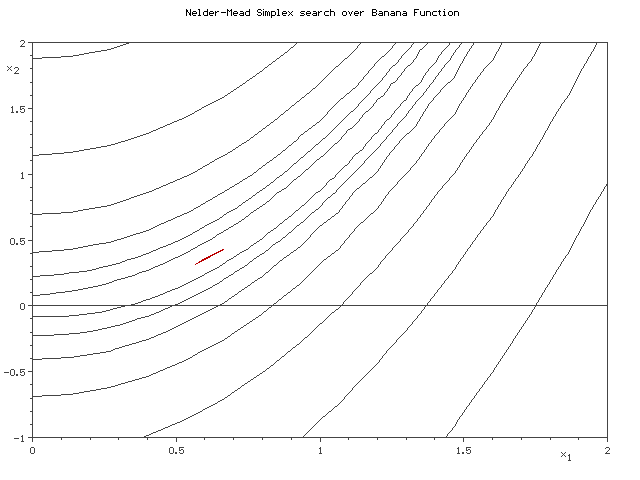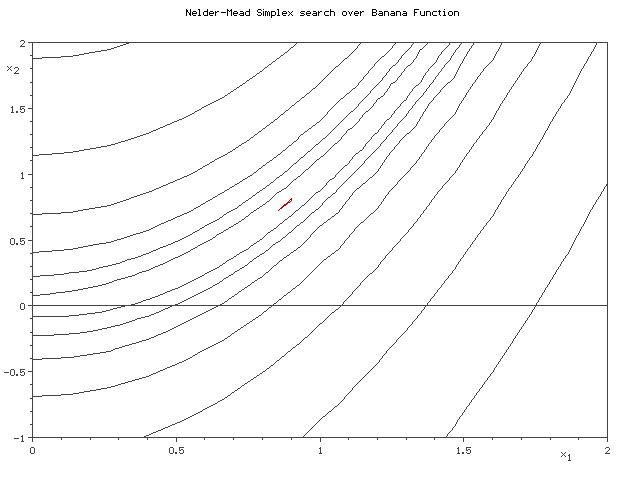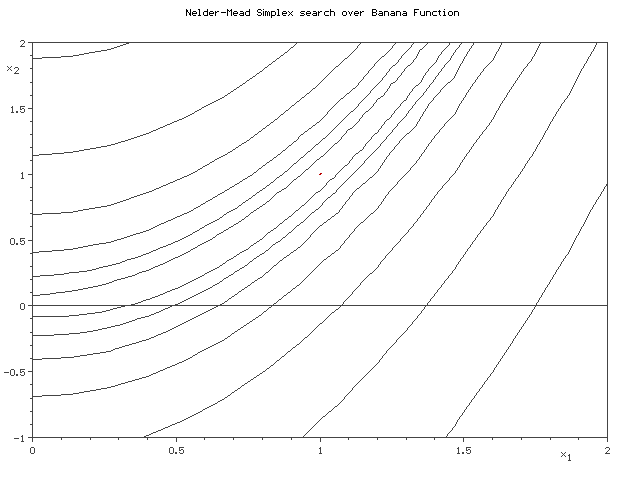
The figure below demonstrates how Nelder-Mead minimizes a two dimensional [http://en.wikipedia.org/wiki/Rosenbrock_function banana function] using a 3 point simplex. | |||
[[Image:2d_Nelder_Mead.gif | Two Dimensional Nelder-Mead Algorithm Converging]]. | |||
= Serial Nelder-Mead Function Minimization Algorithm (Serial Simplex Method)= | |||
For an | For an <tt>n</tt> dimensional function, we start with a simplex of <tt>n+1</tt> arbitrary points in an <tt>n</tt> dimensional space. Let these points be <tt>X0</tt> … <tt>Xn</tt> and the corresponding function values be <tt>Y0</tt> to <tt>Yn</tt>. Thus, to store the entire simplex we will need an <tt>n+1</tt> x <tt>n</tt> array for the points and an array of size <tt>n</tt> for the Function values. Let us briefly discuss what is done in a [http://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method#One_possible_variation_of_the_NM_algorithm single step of the algorithm.] | ||
Single Step of the Nelder Mead Algorithm | |||
At each step of the algorithm we perform | ====Single Step of the Nelder-Mead Algorithm==== | ||
At each step of the algorithm we perform six operations – Ordering, Centroid, Reflection, Expansion, Contraction and Reduction. | |||
*Ordering of Simplex | *Ordering of Simplex | ||
We sort the simplex in ascending order | We sort the simplex using a [http://en.wikipedia.org/wiki/Comparison_sort comparison sort] algorithm in the ascending order of <tt>f(x)</tt>, where <tt>f(x)</tt> is the function to be minimized. i.e. <tt>X0</tt> would be the point with lowest function value and <tt>Xn</tt> would be the point with highest function value. | ||
*Centroid Calculation | *Centroid Calculation | ||
After ordering, we calculate the centroid of all but the worst point <tt>Xn</tt> in the current simplex. | |||
Xcen= 1/N | |||
Xcen = 1/N summation(Xi) for i = 0,1 .... N-1 | |||
*Reflection | *Reflection | ||
After calculating the reflection point, we evaluate the function | Xr = (1+ alpha)Xcen- alpha.Xn | ||
After calculating the reflection point<tt>Xr</tt>, we evaluate the function <tt>Yr</tt> value at this point. If it is an improvement over the minimum function value, we continue in the same direction and calculate the expansion point. | |||
*Expansion | *Expansion | ||
Xe= | |||
If the expansion point is an improvement, then Xe replaces the worst Point | Xe = gamma.Xr+(1-gamma)Xcen | ||
If the expansion point <tt>Xe</tt> is an improvement, then <tt>Xe</tt> replaces the worst Point <tt>Xn</tt> and a new simplex is formed. If the expansion point is not an improvement, then <tt>Xr</tt> replaces <tt>Xn</tt> and the new simplex is calculated. | |||
*Contraction | *Contraction | ||
If Yr is not an improvement over the minimum function value, then we go in the other direction and calculate the contraction point | If <tt>Yr</tt> is not an improvement over the minimum function value, then we go in the other direction and calculate the contraction point <tt>Xc</tt>. | ||
Xc = beta.Xn+(1-beta)Xcen | |||
===Serial | |||
If <tt>Yc</tt> is an improvement over the minimum function value, then <tt>Xc</tt> replaces <tt>Xn</tt> to form the new simplex. | |||
*Reduction | |||
If the contraction point is not an improvement either, then we shrink / reduce the entire simplex towards the best point <tt>X0</tt>. | |||
Xi = X0+ delta (Xi-Xl) ? i=1….N | |||
*Widely used Coefficient Values: | |||
alpha=1 ,gamma=2 ,beta=0.5 ,delta= -0.5 | |||
This process is repeated till we reach a predetermined acceptable value for the [http://en.wikipedia.org/wiki/Maxima_and_minima function minimum]. | |||
Shown below is an example pseudo code for the Serial Nelder-Mead Algorithm. | |||
===Pseudocode for Serial Simplex Method=== | |||
<pre> | <pre> | ||
int N; | int N; | ||
| Line 58: | Line 78: | ||
Sort_Simplex() | Sort_Simplex() | ||
{ | { | ||
Comparison sort | Here we sort the numbers in the ascending order | ||
of the function f(x) which needs to be minimized | |||
Any Comparison sort algorithm for N+1 numbers can be used | |||
} | } | ||
| Line 92: | Line 113: | ||
for i = 0 thru N-1 do | for i = 0 thru N-1 do | ||
for j = 0 thru N do | for j = 0 thru N do | ||
X[i][j] = X[0][j] + | X[i][j] = X[0][j] + delta(X[i][j] – X[i][0]); | ||
end_for | end_for | ||
end_for | end_for | ||
| Line 105: | Line 126: | ||
</pre> | </pre> | ||
=Parallel Nelder Mead Function Minimization Algorithm = | =Parallel Nelder-Mead Function Minimization Algorithm = | ||
==Parallelization at Algorithm Level (Parallel Simplex Method)== | ==Parallelization at Algorithm Level (Parallel Simplex Method)== | ||
Each Processor is assigned parameters corresponding to one point in the simplex. The processors then conduct simplex search steps (as in the serial version) to find a better point. On completion, the processors communicate the new points to form a new simplex. Let us assume that the degree of parallelization is P. Bear in mind that P is may or may not be equal to the number of available processors. For simplicity, let us assume that there are P processors. For 1 processor, this algorithm will be equivalent to the serial algorithm. | Each Processor is assigned parameters corresponding to one point in the simplex. The processors then conduct simplex search steps (as in the serial version) to find a better point. On completion, the processors communicate the new points to form a new simplex. Let us assume that the degree of parallelization is <tt>P</tt>. Bear in mind that <tt>P</tt> is may or may not be equal to the number of available processors. For simplicity, let us assume that there are <tt>P</tt> processors. For 1 processor, this algorithm will be equivalent to the serial algorithm. | ||
We first create a simplex of N+1 points and assign each processor, one of the P worst points and distribute rest of the (N+1 –P) points across all the processors. Then each processor goes through an entire step of the Nelder Mead algorithm. P processors return P improved points, which replace the P worst points in the original simplex. The new simplex is again sorted and divided in the same way. Lee & Wiswall [ | We first create a simplex of <tt>N+1</tt> points and assign each processor, one of the <tt>P</tt> worst points and distribute rest of the <tt>(N+1 –P)</tt> points across all the processors. Then each processor goes through an entire step of the Nelder-Mead algorithm. <tt>P </tt> processors return <tt>P</tt> improved points, which replace the <tt>P</tt> worst points in the original simplex. The new simplex is again sorted and divided in the same way. Lee & Wiswall <sup><span id="3body">[[#3foot|[3]]]</span></sup> provides adequate proof that the parallel algorithm converges as well as the serial algorithm does and that the performance gain reaches saturation after <tt>P = N/2</tt>. Note that this does not take into account parallelism at task level. | ||
==Parallelization at Task Level== | ==Parallelization at Task Level== | ||
The Nelder-Mead algorithm can be parallelized for each individual task, e.g. ordering, centroid calculation, etc. This parallelism is independent of the parallelism at algorithmic level. | |||
===Data Parallel Implementation=== | ===Data Parallel Implementation=== | ||
It can clearly be seen from the serial code that some of the statements like | It can clearly be seen from the serial code that some of the statements like function calculation for every point, calculation of coordinate values for each dimension of the centroid and other points, exhibit DOALL [http://en.wikipedia.org/wiki/Data_parallelism data parallelism], i.e. they are independent of each other and can be performed all at once. The sorting function can be parallelized using a [http://en.wikipedia.org/wiki/Merge_sort Merge Sort] algorithm where we break the entire array into smaller chunks, and sort and combine the result. The code for that can be given as follows, by replacing the for loops by for_all loops: | ||
<pre> | <pre> | ||
int Nprocs; | |||
Nelder_Mead() | Nelder_Mead() | ||
{ | { | ||
| Line 130: | Line 154: | ||
Sort_Simplex() | Sort_Simplex() | ||
{ | { | ||
DECOMP X[i] (CYCLIC,*,Nprocs) // decompose into tasks for each processor | |||
sort X[i] in ascending order of f(x) (function to be minimized) | |||
MERGE sorted outputs of all processors // using any merge-sort algorithm | |||
} | } | ||
| Line 190: | Line 215: | ||
===Shared Memory Implementation=== | ===Shared Memory Implementation=== | ||
In the shared memory | In the [http://en.wikipedia.org/wiki/Shared_memory shared memory] implementation of the algorithm, we use lock () and unlock () commands to make sure that multiple threads do not write to the same memory location at a given time. Only one thread can be in the [http://en.wikipedia.org/wiki/Critical_section critical section] of the program at a given time. | ||
Let us parallelize the sorting, centroid calculation and next point calculation functions. As shown in the code below, the arrays for all the variables need to be shared since multiple threads will be updating it. We use a lock and unlock around it so that no more than one thread tries to modify it at the same time. After waiting for all the updates from different [http://en.wikipedia.org/wiki/Thread_%28computer_science%29 threads] to be done, we proceed ahead. | |||
<pre> | <pre> | ||
shared float Xcen[N]; | |||
shared float Xr[N]; | |||
shared float Xe[N]; | |||
shared float Xc[N]; | |||
shared float X[N+1][N]; | |||
Sort_Simplex() | |||
{ | |||
// break sorting calculation to P threads, | |||
// each thread sorts an array N+1 / P points | |||
for_each_thread | |||
sort myX in ascending order of f(x[i]) (function to be minimized) | |||
LOCK(X) // update centroid using the value from each thread | |||
X = MERGE and sort { X, myX}; | |||
UNLOCK(X); | |||
WAIT_FOR_END(nprocs-1); // wait till entire array gets sorted | |||
} | |||
Calculate_new_point() | |||
{ | |||
// break all calculations to P threads, | |||
// each thread working on N+1 / P points | |||
// reflection | |||
for_each_thread i = 0 thru N do | |||
myXr[i] = (1+alpha)Xcen[i] – alpha*X[N][i]; | |||
LOCK(Xr[i]) // update centroid using the value from each thread | |||
myXr[i] += myXr[i]; | |||
UNLOCK(Xr[i]); | |||
// expansion | |||
for_each_thread i = 0 thru N do | |||
myXe[i] = gamma*Xr[i] + (1- gamma)Xcen[i]; | |||
LOCK(Xe[i]) // update centroid using the value from each thread | |||
myXe[i] += myXe[i]; | |||
UNLOCK(Xe[i]); | |||
//contraction | |||
for_each_thread i = 0 thru N do | |||
myXc[i] = beta*X[N][i] + (1- beta)Xcen[i]; | |||
LOCK(Xc[i]) // update centroid using the value from each thread | |||
myXc[i] += myXc[i]; | |||
UNLOCK(Xc[i]); | |||
WAIT_FOR_END(nprocs-1); // we wait for all threads to update all points | |||
// accept one of the points based on their function values | |||
// as described in the serial section above | |||
// If none of the values is better, shrink or reduce the simplex based on X0 | |||
for_each_thread i = 0 thru N-1 do | |||
for_each_thread j = 0 thru N do | |||
myX[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]); | |||
end_for | |||
end_for | |||
LOCK(X[i][j]) // update centroid using the value from each thread | |||
myX[i][j] += myX[i][j]; | |||
UNLOCK(X[i][j]); | |||
WAIT_FOR_END(nprocs-1); // we wait for all threads to update entire simplex | |||
} | |||
Calculate_Centroid() | Calculate_Centroid() | ||
{ | { | ||
| Line 201: | Line 302: | ||
//The J LOOP and centroid update be broken down into P threads | //The J LOOP and centroid update be broken down into P threads | ||
// with each thread | // with each thread working on N+1/P points | ||
for_each_thread j = 0 thru N-1 do // Centroid of all but worst point | |||
myXcen[i] += X[i][j]; // private variable for each accumulate | myXcen[i] += X[i][j]; // private variable for each accumulate | ||
end | end for | ||
LOCK(Xcen[i]) // update centroid using the value from each thread | LOCK(Xcen[i]) // update centroid using the value from each thread | ||
Xcen[i] += myXcen[i]; | Xcen[i] += myXcen[i]; | ||
| Line 215: | Line 316: | ||
} | } | ||
</pre> | </pre> | ||
===Message Passing Implementation=== | ===Message Passing Implementation=== | ||
In Message passing | In [http://en.wikipedia.org/wiki/Message_passing Message passing] , thread division would be similar to that of the shared memory model, except that each thread has its own private memory and data updates are made by messaging. Here, private variables for each thread will be updated by values received from other threads and each thread will send its own updated value to the others. | ||
<pre> | <pre> | ||
// processes do not complete till all the receives are done. Sends are asynchronous. | |||
Sort_Simplex() | |||
{ | |||
// break sorting calculation to P threads, | |||
// each thread sorts an array N+1 / P points | |||
for_each_thread | |||
sort myX in ascending order of f(x[i]) (function to be minimized) | |||
SEND(X, to all other procs) // update centroid using the value from each thread | |||
X = MERGE and sort { X, myX}; | |||
RECEIVE(X, from all other procs); | |||
} | |||
Calculate_new_point() | |||
{ | |||
// break all calculations to P threads, | |||
// each thread working on N+1 / P points | |||
// reflection | |||
for_each_thread i = 0 thru N do | |||
myXr[i] = (1+alpha)Xcen[i] – alpha*X[N][i]; | |||
SEND(Xr[i], to all other procs) // update centroid using the value from each thread | |||
myXr[i] += Xr[i]; | |||
RECEIVE(Xr[i], from all other procs); | |||
// expansion | |||
for_each_thread i = 0 thru N do | |||
myXe[i] = gamma*Xr[i] + (1- gamma)Xcen[i]; | |||
SEND(Xe[i], to all other procs) // update centroid using the value from each thread | |||
myXe[i] += Xe[i]; | |||
RECEIVE(Xe[i], from all other procs); | |||
//contraction | |||
for_each_thread i = 0 thru N do | |||
myXc[i] = beta*X[N][i] + (1- beta)Xcen[i]; | |||
SEND(Xc[i], to all other procs) // update centroid using the value from each thread | |||
myXc[i] += Xc[i]; | |||
RECEIVE(Xc[i], from all other procs); | |||
// accept one of the points based on their function values | |||
// as described in the serial section above | |||
// If none of the values is better, shrink or reduce the simplex based on X0 | |||
for_each_thread i = 0 thru N-1 do | |||
for_each_thread j = 0 thru N do | |||
myX[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]); | |||
end_for | |||
end_for | |||
SEND(X[i][j], to all other procs) // update centroid using the value from each thread | |||
myX[i][j] += X[i][j]; | |||
RECEIVE (X[i][j], from all other procs); | |||
} | |||
Calculate_Centroid() | Calculate_Centroid() | ||
{ | { | ||
| Line 230: | Line 395: | ||
// with each thread workingon N+1/P points | // with each thread workingon N+1/P points | ||
for_each_thread j = 0 thru N-1 do // Centroid of all but worst point | |||
myXcen[i] += X[i][j]; // private variable for each accumulate | myXcen[i] += X[i][j]; // private variable for each accumulate | ||
end | end for | ||
SEND(Xcen[i], to all other procs) // send updated values to other processors | SEND(Xcen[i], to all other procs) // send updated values to other processors | ||
Xcen[i] += myXcen[i]; | Xcen[i] += myXcen[i]; | ||
| Line 242: | Line 407: | ||
</pre> | </pre> | ||
=Conclusion= | |||
We have seen here that a highly serial algorithm like Nelder Mead can be parallelized using various methods. The most efficient approach to this would be to parallelize it at algorithmic level first, which provides faster convergence. For any program or application, choice of algorithm (efficiency, run time, memory usage) is most important to performance. A poor choice of algorithm will give sub standard performance compared to a good algorithm, assuming both of them are parallelized at task level. | |||
Once algorithm level parallelization is done, individual tasks can be parallelized using any of the methods described above, depending on the underlying hardware available. Data parallel implementation is suitable for vector processors or GPUs while the shared memory implementation can be used with any bus based or distributed shared memory system. The message passing model has lot of communication overhead but does not need a shared memory between processors. | |||
=References= | =References= | ||
<span id="1foot">[[#1body|1.]]</span> http://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method <br> | <span id="1foot">[[#1body|1.]]</span> [http://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method Nelder-Mead Method] <br> | ||
<span id="2foot">[[#2body|2.]]</span> Nelder, J. A., and R. Mead (1965): “A Simplex Method for Function Minimization,” Computer Journal, 7, 308–313 <br> | <span id="2foot">[[#2body|2.]]</span> Nelder, J. A., and R. Mead (1965): “A Simplex Method for Function Minimization,” Computer Journal, 7, 308–313 <br> | ||
<span id="3foot">[[#3body|3.]]</span> Donghoon Lee, Matthew Wiswall (2007):"A Parallel Implementation of the Simplex Function Minimization Routine," Journal, Computational Economics, Volume 30 Issue 2 | <span id="3foot">[[#3body|3.]]</span> Donghoon Lee, Matthew Wiswall (2007):"A Parallel Implementation of the Simplex Function Minimization Routine," Journal, Computational Economics, Volume 30 Issue 2 <br> | ||
<span id="4foot">[[#4body|4.]]</span> CSC/ECE 506 Spring 2011 Lecture 7 Notes, by Dr. Edward Gehringer <br> | <span id="4foot">[[#4body|4.]]</span> CSC/ECE 506 Spring 2011 Lecture 7 Notes, by Dr. Edward Gehringer <br> | ||
Latest revision as of 17:07, 12 April 2011
Introduction
The Nelder-Mead Algorithm is a simplex method for function minimization developed by J. A. Nelder and R. Mead in 1965[2]. The method is used for minimizing an N dimensional function, by comparing the function values at n+1 vertices of a simplex, followed by the replacement of the vertex with highest function value by another vertex having a lower function value. The algorithm, by itself is highly serial in nature.
In this article, we will discuss the Serial Nelder-Mead Algorithm and its parallelization at Algorithmic level and Task Level. For the Algorithmic level parallelism, we will look at a method to replace more than one point from the simplex in a single iteration. For task level parallelism, we will pick individual tasks from the algorithm and try to parallelize them using methods like data parallel programming, shared memory programming and message passing. The choice of methods for task level parallelism largely depends on the underlying hardware and the computation / communication overhead for each of the methods.
The figure below demonstrates how Nelder-Mead minimizes a two dimensional banana function using a 3 point simplex.
Serial Nelder-Mead Function Minimization Algorithm (Serial Simplex Method)
For an n dimensional function, we start with a simplex of n+1 arbitrary points in an n dimensional space. Let these points be X0 … Xn and the corresponding function values be Y0 to Yn. Thus, to store the entire simplex we will need an n+1 x n array for the points and an array of size n for the Function values. Let us briefly discuss what is done in a single step of the algorithm.
Single Step of the Nelder-Mead Algorithm
At each step of the algorithm we perform six operations – Ordering, Centroid, Reflection, Expansion, Contraction and Reduction.
- Ordering of Simplex
We sort the simplex using a comparison sort algorithm in the ascending order of f(x), where f(x) is the function to be minimized. i.e. X0 would be the point with lowest function value and Xn would be the point with highest function value.
- Centroid Calculation
After ordering, we calculate the centroid of all but the worst point Xn in the current simplex.
Xcen = 1/N summation(Xi) for i = 0,1 .... N-1
- Reflection
Xr = (1+ alpha)Xcen- alpha.Xn
After calculating the reflection pointXr, we evaluate the function Yr value at this point. If it is an improvement over the minimum function value, we continue in the same direction and calculate the expansion point.
- Expansion
Xe = gamma.Xr+(1-gamma)Xcen
If the expansion point Xe is an improvement, then Xe replaces the worst Point Xn and a new simplex is formed. If the expansion point is not an improvement, then Xr replaces Xn and the new simplex is calculated.
- Contraction
If Yr is not an improvement over the minimum function value, then we go in the other direction and calculate the contraction point Xc.
Xc = beta.Xn+(1-beta)Xcen
If Yc is an improvement over the minimum function value, then Xc replaces Xn to form the new simplex.
- Reduction
If the contraction point is not an improvement either, then we shrink / reduce the entire simplex towards the best point X0. Xi = X0+ delta (Xi-Xl) ? i=1….N
- Widely used Coefficient Values:
alpha=1 ,gamma=2 ,beta=0.5 ,delta= -0.5
This process is repeated till we reach a predetermined acceptable value for the function minimum.
Shown below is an example pseudo code for the Serial Nelder-Mead Algorithm.
Pseudocode for Serial Simplex Method
int N;
float X[N+1][N+1]; // N+1 Points, each with N+1 coordinates.
float Y[N+1]; // Function values for N+1 points. (this is a function of X)
float Y_max_allowed; // termination condition
float Ycen, Xcen[N+1]; // centroid
float Yr, Xr[N+1]; // reflection point
float Yc, Xc[N+1]; // contration point
float Ye, Xe[N+1]; // expansion point
Nelder_Mead()
{
done = 0;
Sort_Simplex();
while(!done)
{
Calculate_Centroid();
Calculate_new_point();
Sort_Simplex();
Check_done();
}
}
Sort_Simplex()
{
Here we sort the numbers in the ascending order
of the function f(x) which needs to be minimized
Any Comparison sort algorithm for N+1 numbers can be used
}
Calculate_Centroid()
{
for i = 0 thru N do // For all Dimensions
for j = 0 thru N-1 do // Centroid of all but worst point
Xcen[i] += X[i][j];
end for
Xcen[i] /= N;
end for
}
Calculate_new_point()
{
// reflection
for i = 0 thru N do
Xr[i] = (1+alpha)Xcen[i] – alpha*X[N][i];
// expansion
for i = 0 thru N do
Xe[i] = gamma*Xr[i] + (1- gamma)Xcen[i];
//contraction
for i = 0 thru N do
Xe[i] = beta*X[N][i] + (1- beta)Xcen[i];
// accept one of the points based on their function values
// as described in the section above
// If none of the values is better, shrink the simplex based on X0
for i = 0 thru N-1 do
for j = 0 thru N do
X[i][j] = X[0][j] + delta(X[i][j] – X[i][0]);
end_for
end_for
}
Check_done()
{
// stop if the lowest function value is small enough
if(Y[0] <= Y_max_allowed)
done = 1;
}
Parallel Nelder-Mead Function Minimization Algorithm
Parallelization at Algorithm Level (Parallel Simplex Method)
Each Processor is assigned parameters corresponding to one point in the simplex. The processors then conduct simplex search steps (as in the serial version) to find a better point. On completion, the processors communicate the new points to form a new simplex. Let us assume that the degree of parallelization is P. Bear in mind that P is may or may not be equal to the number of available processors. For simplicity, let us assume that there are P processors. For 1 processor, this algorithm will be equivalent to the serial algorithm. We first create a simplex of N+1 points and assign each processor, one of the P worst points and distribute rest of the (N+1 –P) points across all the processors. Then each processor goes through an entire step of the Nelder-Mead algorithm. P processors return P improved points, which replace the P worst points in the original simplex. The new simplex is again sorted and divided in the same way. Lee & Wiswall [3] provides adequate proof that the parallel algorithm converges as well as the serial algorithm does and that the performance gain reaches saturation after P = N/2. Note that this does not take into account parallelism at task level.
Parallelization at Task Level
The Nelder-Mead algorithm can be parallelized for each individual task, e.g. ordering, centroid calculation, etc. This parallelism is independent of the parallelism at algorithmic level.
Data Parallel Implementation
It can clearly be seen from the serial code that some of the statements like function calculation for every point, calculation of coordinate values for each dimension of the centroid and other points, exhibit DOALL data parallelism, i.e. they are independent of each other and can be performed all at once. The sorting function can be parallelized using a Merge Sort algorithm where we break the entire array into smaller chunks, and sort and combine the result. The code for that can be given as follows, by replacing the for loops by for_all loops:
int Nprocs;
Nelder_Mead()
{
done = 0;
Sort_Simplex();
while(!done)
{
Calculate_Centroid();
Calculate_new_point();
Sort_Simplex();
Check_done();
}
}
Sort_Simplex()
{
DECOMP X[i] (CYCLIC,*,Nprocs) // decompose into tasks for each processor
sort X[i] in ascending order of f(x) (function to be minimized)
MERGE sorted outputs of all processors // using any merge-sort algorithm
}
Calculate_Centroid()
{
DECOMP X[i][j](CYCLIC,*,Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do // For all Dimensions
DECOMP X[i][j](*,CYCLIC, Nprocs) // decompose into tasks for each processor
for_all j = 0 thru N-1 do // Centroid of all but worst point
myXcen[i] += X[i][j]; // private variable for each accumulate
end for_all
REDUCE(myXcen[i],Xcen[i],ADD) ; // reduction operator for Centroid
Xcen[i] /= N;
end for
}
Calculate_new_point()
{
// reflection
DECOMP Xr[i] (CYCLIC, Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do
Xr[i] = (1+alpha)Xcen[i] – alpha*X[N][i];
// expansion
DECOMP Xe[i] (CYCLIC, Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do
Xe[i] = gamma*Xr[i] + (1- gamma)Xcen[i];
//contraction
DECOMP Xc[i] (CYCLIC, Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N do
Xc[i] = beta*X[N][i] + (1- beta)Xcen[i];
// accept one of the points based on their function values
// as described in the serial section above
// If none of the values is better, shrink or reduce the simplex based on X0
DECOMP X[i][j](CYCLIC,*,Nprocs) // decompose into tasks for each processor
for_all i = 0 thru N-1 do
DECOMP X[i][j](*,CYCLIC, Nprocs) // decompose into tasks for each processor
for_all j = 0 thru N do
X[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]);
end_for_all
end_for_all
}
Check_done()
{
// stop if the lowest function value is small enough
if(Y[0] <= Y_max_allowed)
done = 1;
}
In the shared memory implementation of the algorithm, we use lock () and unlock () commands to make sure that multiple threads do not write to the same memory location at a given time. Only one thread can be in the critical section of the program at a given time. Let us parallelize the sorting, centroid calculation and next point calculation functions. As shown in the code below, the arrays for all the variables need to be shared since multiple threads will be updating it. We use a lock and unlock around it so that no more than one thread tries to modify it at the same time. After waiting for all the updates from different threads to be done, we proceed ahead.
shared float Xcen[N];
shared float Xr[N];
shared float Xe[N];
shared float Xc[N];
shared float X[N+1][N];
Sort_Simplex()
{
// break sorting calculation to P threads,
// each thread sorts an array N+1 / P points
for_each_thread
sort myX in ascending order of f(x[i]) (function to be minimized)
LOCK(X) // update centroid using the value from each thread
X = MERGE and sort { X, myX};
UNLOCK(X);
WAIT_FOR_END(nprocs-1); // wait till entire array gets sorted
}
Calculate_new_point()
{
// break all calculations to P threads,
// each thread working on N+1 / P points
// reflection
for_each_thread i = 0 thru N do
myXr[i] = (1+alpha)Xcen[i] – alpha*X[N][i];
LOCK(Xr[i]) // update centroid using the value from each thread
myXr[i] += myXr[i];
UNLOCK(Xr[i]);
// expansion
for_each_thread i = 0 thru N do
myXe[i] = gamma*Xr[i] + (1- gamma)Xcen[i];
LOCK(Xe[i]) // update centroid using the value from each thread
myXe[i] += myXe[i];
UNLOCK(Xe[i]);
//contraction
for_each_thread i = 0 thru N do
myXc[i] = beta*X[N][i] + (1- beta)Xcen[i];
LOCK(Xc[i]) // update centroid using the value from each thread
myXc[i] += myXc[i];
UNLOCK(Xc[i]);
WAIT_FOR_END(nprocs-1); // we wait for all threads to update all points
// accept one of the points based on their function values
// as described in the serial section above
// If none of the values is better, shrink or reduce the simplex based on X0
for_each_thread i = 0 thru N-1 do
for_each_thread j = 0 thru N do
myX[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]);
end_for
end_for
LOCK(X[i][j]) // update centroid using the value from each thread
myX[i][j] += myX[i][j];
UNLOCK(X[i][j]);
WAIT_FOR_END(nprocs-1); // we wait for all threads to update entire simplex
}
Calculate_Centroid()
{
for_all i = 0 thru N do // For all Dimensions
//The J LOOP and centroid update be broken down into P threads
// with each thread working on N+1/P points
for_each_thread j = 0 thru N-1 do // Centroid of all but worst point
myXcen[i] += X[i][j]; // private variable for each accumulate
end for
LOCK(Xcen[i]) // update centroid using the value from each thread
Xcen[i] += myXcen[i];
UNLOCK(Xcen[i]);
WAIT_FOR_END(nprocs-1); // we wait for all threads to update the centroid
Xcen[i] /= N;
end for
}
Message Passing Implementation
In Message passing , thread division would be similar to that of the shared memory model, except that each thread has its own private memory and data updates are made by messaging. Here, private variables for each thread will be updated by values received from other threads and each thread will send its own updated value to the others.
// processes do not complete till all the receives are done. Sends are asynchronous.
Sort_Simplex()
{
// break sorting calculation to P threads,
// each thread sorts an array N+1 / P points
for_each_thread
sort myX in ascending order of f(x[i]) (function to be minimized)
SEND(X, to all other procs) // update centroid using the value from each thread
X = MERGE and sort { X, myX};
RECEIVE(X, from all other procs);
}
Calculate_new_point()
{
// break all calculations to P threads,
// each thread working on N+1 / P points
// reflection
for_each_thread i = 0 thru N do
myXr[i] = (1+alpha)Xcen[i] – alpha*X[N][i];
SEND(Xr[i], to all other procs) // update centroid using the value from each thread
myXr[i] += Xr[i];
RECEIVE(Xr[i], from all other procs);
// expansion
for_each_thread i = 0 thru N do
myXe[i] = gamma*Xr[i] + (1- gamma)Xcen[i];
SEND(Xe[i], to all other procs) // update centroid using the value from each thread
myXe[i] += Xe[i];
RECEIVE(Xe[i], from all other procs);
//contraction
for_each_thread i = 0 thru N do
myXc[i] = beta*X[N][i] + (1- beta)Xcen[i];
SEND(Xc[i], to all other procs) // update centroid using the value from each thread
myXc[i] += Xc[i];
RECEIVE(Xc[i], from all other procs);
// accept one of the points based on their function values
// as described in the serial section above
// If none of the values is better, shrink or reduce the simplex based on X0
for_each_thread i = 0 thru N-1 do
for_each_thread j = 0 thru N do
myX[i][j] = X[0][j] + gamma(X[i][j] – X[i][0]);
end_for
end_for
SEND(X[i][j], to all other procs) // update centroid using the value from each thread
myX[i][j] += X[i][j];
RECEIVE (X[i][j], from all other procs);
}
Calculate_Centroid()
{
for_all i = 0 thru N do // For all Dimensions
//The J LOOP and centroid update be broken down into P threads
// with each thread workingon N+1/P points
for_each_thread j = 0 thru N-1 do // Centroid of all but worst point
myXcen[i] += X[i][j]; // private variable for each accumulate
end for
SEND(Xcen[i], to all other procs) // send updated values to other processors
Xcen[i] += myXcen[i];
RECEIVE(Xcen[i], from all other procs); // get updated values from other processors
Xcen[i] /= N;
end for
}
Conclusion
We have seen here that a highly serial algorithm like Nelder Mead can be parallelized using various methods. The most efficient approach to this would be to parallelize it at algorithmic level first, which provides faster convergence. For any program or application, choice of algorithm (efficiency, run time, memory usage) is most important to performance. A poor choice of algorithm will give sub standard performance compared to a good algorithm, assuming both of them are parallelized at task level.
Once algorithm level parallelization is done, individual tasks can be parallelized using any of the methods described above, depending on the underlying hardware available. Data parallel implementation is suitable for vector processors or GPUs while the shared memory implementation can be used with any bus based or distributed shared memory system. The message passing model has lot of communication overhead but does not need a shared memory between processors.
References
1. Nelder-Mead Method
2. Nelder, J. A., and R. Mead (1965): “A Simplex Method for Function Minimization,” Computer Journal, 7, 308–313
3. Donghoon Lee, Matthew Wiswall (2007):"A Parallel Implementation of the Simplex Function Minimization Routine," Journal, Computational Economics, Volume 30 Issue 2
4. CSC/ECE 506 Spring 2011 Lecture 7 Notes, by Dr. Edward Gehringer