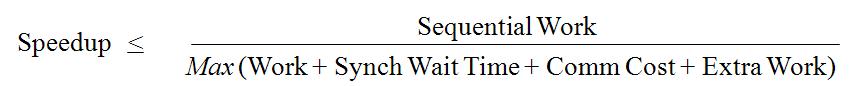CSC/ECE 506 Fall 2007/wiki1 12 dp3: Difference between revisions
No edit summary |
|||
| (185 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Sections 1.3.3 and 1.3.4: Most changes here are probably related to performance metrics. Cite other models for measuring artifacts such as data-transfer time, overhead, occupancy, and communication cost. Focus on the models that are most useful in practice. | |||
== Communication and Replication == | |||
In this section, we describe two terms Communication and [http://en.wikipedia.org/wiki/Replication_(computer_science) Replication], simultaneously we also make distinction between these two terms. | |||
Communication between any two [http://en.wikipedia.org/wiki/Process_(computing) processes] is said to occur when data written by one process is read by second process. This causes a data transfer between the processes however, if data is just stored at one process (because initially data was configured to be on this process or it was too large to fit at any other place) and transfer only makes another copy of the data at second process then it called replication. | |||
For example, on processor’s request of data if we copy something from main memory and put it in cache this operation is replication of data. On the contrast if a data is produced by a sender process and it is transferred to a receiver process by message passing then it is an example of communication. | |||
Communication and replication both involves data transfer, which can be defined as transfer of data across different memory locations. For interprocess(or) communication the data is transferred across the memory local to the communicating processor or from a remote storage device. When a miss occurs in cache, the data is transferred from the memory to the cache. In case, where the cache content, as a result of replication, is updated or changed, these changes must be transported to all the other hidden replicas. This is another aspect of data transfer. | |||
== Performance == | |||
=== Introduction === | |||
In this section, we briefly discuss various importance aspects of performance measurement in parallel computer architecture and basic performance metrics. | |||
As we already know, performance measurement is one of the fundamental issues in [http://en.wikipedia.org/wiki/Uniprocessor uniprocessor system] where architects focus on improving performance by reducing execution time of standard programs called benchmarks. They use several techniques such as minimizing memory access time, designing hardware which can execute many instruction in parallel and possibly faster ([http://en.wikipedia.org/wiki/Instruction_level_parallelism micro level parallelism] extraction) etc. Performance measurement is more serious concern in parallel computing because apart from computing performance measurement we also need to analyze communication cost as data is shared among many processors and processes (possibly on different processors) need to communicate efficiently, coherently and correctly. | |||
To make our point more precise, let us consider the following example: | |||
:Assume we want to run a program which takes 100sec on uniprocessor. However, we also know that the full program can be decomposed in many processes and these processes can be run on different machine. So basically, in best case we expect the speed up of <tt>n</tt> where <tt>n</tt> is the number of processors available. We have divided the computing load but these processes can not run independently to achieve the completion. To run the program correctly, these processes do need to communicate to each other for data sharing, [http://en.wikipedia.org/wiki/Synchronization synchronization] etc. Hence, there is communication overhead involved in parallel computing. | |||
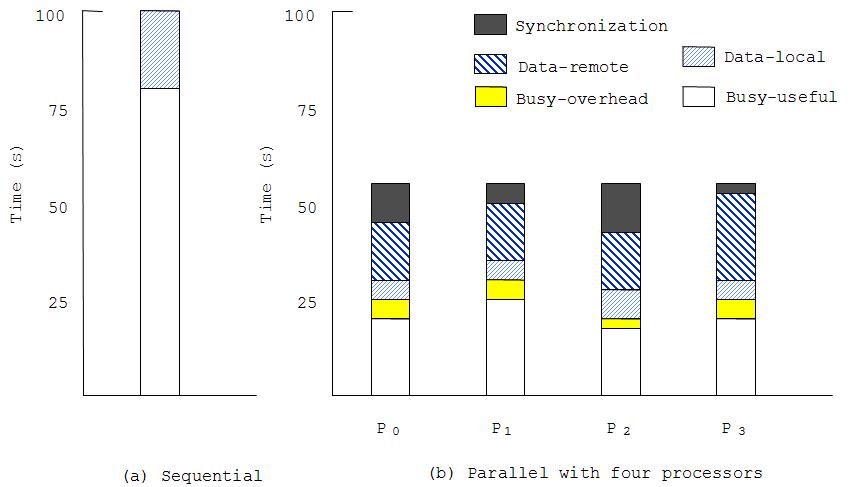
[http://pg.ece.ncsu.edu/mediawiki/index.php/Image:P02.jpg Following figure] ([http://www.cs.berkeley.edu/~culler/cs258-s99/ reference]) helps in understanding how parallel processers typically spend their execution time on different activities like: local/remote data access, computing, synchronization and other work. | |||
[[Image: P02.jpg| P02.jpg]] | |||
A sequential program takes 100 sec to run the program, in this hypothetical example it is assumed that 80% time is busy-useful (i.e.execution of instructions) time however rest 20% of the time processor spends in accessing local data. | |||
Four parallel processors solve the same problem in 55 seconds (speed up of 1.8 instead of expected speed up of 4). Parallel processors spend time in accessing data at both locations : remote and local. These processors execute instructions which we call busy useful time and moreover they synchronize with each other to execute the program correctly. However in such a parallel computing environment, processors execute some instructions/work which are not needed if program is run sequentially, time spent in such activities is called busy-overhead time. Such type of work is also called 'extra work' which we will discuss shortly. | |||
Clearly, a wise architect would not like to have any parallel system where communication overheads overwhelm speed up achieved by dividing the computing-load. In other words, diving computing load on different processors is good idea only when communication costs do not shoot up too much. Similarly, in order to reduce communication cost one should not kill the inherent parallelism available in the program. | |||
[http://en.wikipedia.org/wiki/Speedup Speedup] ([http://www.cs.berkeley.edu/~culler/cs258-s99/ reference]) gain by parallel computing has to take into the account the synchronization time, communication cost and extra work apart from computing work. So, speed up can be expressed as following: | |||
[[Image: P01.jpg| P01.jpg]] | |||
In the equation above, 'extra work' is work done by processors other than computation, synchronization and communication. This might include: | |||
:Computing a good partition for a particular problem. | |||
:Using redundant computation to avoid communication. | |||
:Task, data and process management overhead etc. | |||
Hence, it is obvious that in order to increase the speed up (improve performance), architects would focus on all the factors appearing in the denominator of above equation. Therefore, we need to consider various design trade-offs while analyzing performance of parallel computing architecture. | |||
There are three basic performance metrics. | |||
* [http://en.wikipedia.org/wiki/Latency_(engineering) Latency] : Time taken by an operation to get completed. ( measured as seconds per operation) | |||
* [http://en.wikipedia.org/wiki/Bandwidth Bandwidth]: The rate at which operations are executed. (measured as operations per second) | |||
* Cost: Cost is basically impact of operations on total execution time of the program. (measured as latency times number of operations) | |||
In uniprocessor system, bandwidth is simply reciprocal of latency however, in parallel computing many operations are performed concurrently so relationship among performance metrics is not simple.In parallel computing, we need to consider the performance for communication operations along with computing operations. | |||
We list three [http://pg.ece.ncsu.edu/mediawiki/index.php/CSC/ECE_506_Fall_2007/wiki1_12_dp3#Artifacts_of_Measuring_Performance artifacts of measuring performance] and since data transfer operations are the most frequent type of communication operation, discussion on the same appears first. | |||
=== Artifacts of Measuring Performance === | |||
*[http://pg.ece.ncsu.edu/mediawiki/index.php/CSC/ECE_506_Fall_2007/wiki1_12_dp3#Data_Transfer Data Transfer] | |||
*[http://pg.ece.ncsu.edu/mediawiki/index.php/CSC/ECE_506_Fall_2007/wiki1_12_dp3#Overhead_and_Occupancy Overhead and Occupancy] | |||
*[http://pg.ece.ncsu.edu/mediawiki/index.php/CSC/ECE_506_Fall_2007/wiki1_12_dp3#Communication_Cost Communication Cost] | |||
==== Data Transfer ==== | |||
For any data transfer we would like to estimate the time it consumes, so that we can improve the overall performance of the system by reducing data transfer time. To estimate the data transfer time a simple ''[http://en.wikipedia.org/wiki/Linear_model linear model]'' is used ( [http://www.cs.berkeley.edu/~culler/cs258-s99/#lectures referenced lecture material]): | |||
<tt><center> '''Total Transfer Time (T) = Start-up Time (T<sub>0</sub>) + Data Transfer Time (T<sub>D</sub>)'''</center> </tt> | |||
Total transfer time has two components: | |||
1. A constant term (T0) which is called start up cost. We will shortly return to this with more details. | |||
2. Data transfer time, which is estimated as following: | |||
<tt><center>'''Data Transfer Time (T<sub>D</sub>)) = Size of Data (n) / Bandwidth (B)'''</center></tt> | |||
Bandwidth (B) is also called data transfer rate. | |||
To have better understanding of the model, we should be clear about the following points: | |||
* If we have only one pair of host then data transfer rate is simply the bandwidth of the link connecting those hosts. | |||
* However if there are many hosts between the source host and destination host, bottleneck is the link with lowest bandwidth. | |||
Important point to note is that the '''achievable bandwidth''' depends on the transfer size, that is why sometimes bandwidth (<tt>'''B'''</tt>) is called as '''peak bandwidth'''. For example: | |||
::Suppose we have two hosts connected by a link with bandwidth of 20MB/s and start up cost of communication is 2 micro seconds. We want to transfer an image of size 40MB then the total transfer time is 2 seconds plus 2 micro seconds. Given the available peak bandwidth of 20MB/s, one might have expected to complete the transfer in 2 seconds achieving the peak bandwidth but start up cost prohibits this. Clearly as you increase the amount of data achievable bandwidth approaches the asymptotic rate of bandwidth (B), in fact start up cost determines how fast the asymptotic rate would be achieved. | |||
As a special case, the amount of data required to achieve half of peak bandwidth (<tt>'''B'''</tt>) is equal to <tt>'''T<sub>0</sub> X B'''</tt>. This is also called '''half-power point'''. Please note that printed version of the [http://www.amazon.com/Parallel-Computer-Architecture-Hardware-Software/dp/1558603433 text-book] has erroneous formula for calculating half-power point. | |||
Now, we discuss first part of total transfer-time i.e. start-up cost. Notice that <tt>'''T<sub>0</sub>'''</tt> is a constant term for a particular data transfer,but it might vary as we consider data transfer over different entities. ''For example'', in memory operation start up cost is memory access time. In message passing the start up cost can be estimated as time taken by fist bit to reach destination. For pipelined operations, start up cost is simply time taken to fill up the pipeline. For bus transactions it is arbitration and command phases.<br> | |||
As parallel computing has advanced, one of the major focuses has been to ''reduce start up cost''. There are many ways to do so; we describe few of them here. As stated earlier start up cost for memory operations is basically the memory access time. To reduce memory access time, architects have introduced costly (hence small size) but fast storage area called [http://en.wikipedia.org/wiki/Cache cache]. Depending upon the [http://en.wikipedia.org/wiki/Memory_locality spatial and temporal locality] cache is filled with useful items and hence processor does not have to go to memory (long [http://en.wikipedia.org/wiki/Memory_latency latency] ) every time it needs data. | |||
Average access time is governed by the following formula [http://www.amazon.com/Computer-Architecture-Fourth-Quantitative-Approach/dp/0123704901 Computer Architecture: A Quantitative Approach, Appendix C]: | |||
<tt><center> '''Average memory access time = Hit time for the cache + (Miss Rate X Miss Penalty)'''</center></tt> | |||
Therefore architects often try to reduce all three components by adopting [http://citeseer.ist.psu.edu/kowarschik03overview.html different cache optimization] like: multilevel cache, larger blocks size, higher associatively etc. | |||
We quote the access time of cache and main memory to see how beneficial it might be to introduce cache if we manage to get considerably high hit rates. | |||
Cache access time is typically 0.5-25 ns while for the main memory it is 50-250 ns, so we can decrease start-up cost considerably by having such a memory hierarchy. Bandwidth for caches range around 5,000-20,000 MB/sec but for memory its as low as 2,500-10,000MB/sec. [http://www.amazon.com/Computer-Architecture-Fourth-Quantitative-Approach/dp/0123704901 Computer Architecture: A Quantitative Approach, Appendix C] | |||
Similarly for ''bus transactions'', start up cost is time spent during arbitration and command phases, suppose on a 3.6 GHz Intel Xeon machine (year 2004) it takes 3 cycles to arbitrate the bus and present the address the start up cost is around 0.83 nano seconds. However assuming that around year 1994-95 it took same 3 cycles on Alpha 21064A 0.3 GHz processor we can see that start up cost has been reduced by more than 10 times. [http://www.amazon.com/Computer-Architecture-Fourth-Quantitative-Approach/dp/0123704901 Computer Architecture: A Quantitative Approach, Chapter 1] | |||
''Pipelining'' is another way to reduce the data transfer time, for pipelined systems filling up the pipeline is the total start up cost. Though it seems that introducing pipeline adds extra start up cost, however more importantly pipeline allows multiple operations to take place concurrently and this indeed helps in achieving higher bandwidth.[http://www.amazon.com/Computer-Architecture-Fourth-Quantitative-Approach/dp/0123704901 Computer Architecture: A Quantitative Approach, Appendix A] | |||
Startup cost calculation is many times challenging, with enhancement in technology focus is too reduce the start-up cost and increase bandwidth. | |||
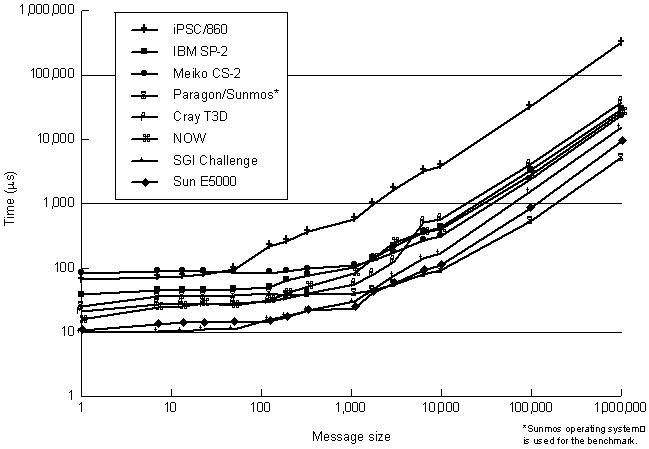
[http://pg.ece.ncsu.edu/mediawiki/images/3/37/P03.jpg Next plot] (on log-log scale) shows time for message passing operation for several machines as a function of message size [http://www.amazon.com/Parallel-Computer-Architecture-Hardware-Software/dp/1558603433 source]. We notice the start-up costs for different machines vary a lot (nearly spread over an order of magnitude). These start up costs vary a lot and total transfer size is non linear function of message size for small amount of data, contrary to linear data transfer model. For big size data transfer we get almost linear relationship. The bandwidth can be calculated by slope of the line. | |||
[[Image:P03.jpg | Time for message passing operation versus message size ]], | |||
Quoting other figures, | |||
'''iPSC/2''' machine has start up cost of 700 micro seconds and '''CRAY T3D (PVM)''' machine has start up cost of 21 micro seconds, we can clearly see the trends that within one decade start up cost has dropped by an order of magnitude. '''NOW''' machine has start up cost of just 16 micro seconds. Basically these improvements are essentially due to improvement in cycle time. | |||
Similar trends can be observed in 'Maximum Bandwidth' achievable on each machine for data transfer. For '''nCUBE/2''' machine maximum bandwidth was 2 MB/s but relatively advanced machines like '''SP2''' has bandwidth of 40 MB/s. | |||
: However, this data transfer model has few shortcomings too. | |||
This model does not indicate when the next operation can be performed. Estimating time interval between two operations is particularly very useful because bandwidth depends on how frequently operations can be initiated. | |||
This model also does not tell about whether other useful work can be done during transfer or not. | |||
This model is easy to understand but it is not very suitable for architectural evaluation. For network transactions, total message time is difficult to measure unless there is a global clock as the send and receive usually happen on different processors.So, transaction time is usually measured by doing a echo test (i.e. one processor sends the data and waits until it receives a message). But this is reliable only if receive is posted before message arrives hence measuring transaction time is very challenging (and not always accurate) in this transfer model. | |||
::In this section we discussed different aspects of data transfer model.In parallel computing environment, data transfers usually take place across the network and it is invoked by processor through the communication assist. Therefore, now we need to look at how communication costs are estimated and what are the important factors to consider? | |||
==== Overhead and Occupancy ==== | |||
One of the three components of Processor execution time, apart from ''Computation Time and Idle Time'', is ''Communication Time''. Communication time is the time spent by the processor on exchanging messages with another process(or). There can be two different types of communication, i.e. interprocessor and intraprocessor. In interprocessor communication the two communicating tasks are handled by two different processors. While in intraprocessor communication the communicating tasks are handled by the same processor. Generally both intraprocessor and interprocessor communication costs the same, provided the former is not highly optimized. | |||
Communication time is function of number of bytes (n) transferred across. It can be given as below | |||
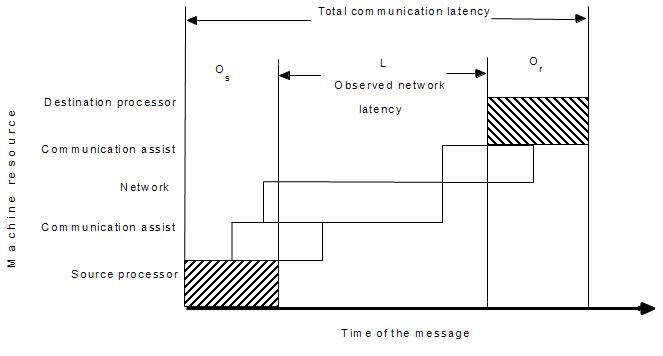
<tt><center> '''T(n) = Overhead + Occupancy + Network Delay + Message Size / Bandwidth + Delay due to Contention'''</center></tt> | |||
[[Image:time.jpg]] | |||
Source [http://www.cs.berkeley.edu/~culler/cs258-s99/ Lecture :Culler] | |||
Communication Overhead includes time spent on | |||
*Create messages | |||
*Execute communications protocols | |||
*Physically send messages | |||
*Run through the protocol sets and decode the message on the receiving node. | |||
During this period the processor cannot do any useful or computational work. Parallel programs, running on different processors need to coordinate their work among themselves. This results in increased rate of interprocessor communication, which in turn increases the net overhead cost. | |||
Occupancy is the time spent at the slowest component in the communication assist and it affects performance in couple of ways. It delays the current request and indirectly contributes to the delays of subsequent requests. The occupancy gets to set the upper limit on how frequently communication operation can be initiated by the processor. | |||
''Some of the recent trends/designs helped reduce these communication costs. [http://en.wikipedia.org/wiki/Blue_Gene IBM Blue Gene (L)] uses [http://www-03.ibm.com/industries/education/doc/content/bin/WhitepaperIBMBlueGenev7.0.pdf Global Collective Network], which carries out operations within the network itself. This saves the processors time to decode messages with intermediate values, calculate new intermediate values, create new messages, and send them on to other nodes. The overhead now is primarily because of communication protocol. It also has a dedicated communications network, [http://www-03.ibm.com/industries/education/doc/content/bin/WhitepaperIBMBlueGenev7.0.pdf Global Barrier and Interrupt Network], to speed up task-to-task coordination activities. IBM BG/L also employs [http://www-03.ibm.com/industries/education/doc/content/bin/WhitepaperIBMBlueGenev7.0.pdf Torus Network], which results in linear growth of the path length while nodes (processors) scale as a cube. Torus Network also gives the ability to send messages in either direction, something like a ring network and hence reduces the distance between furthest points to half. This in turn reduces the network delays.'' | |||
[[Image:torus1.jpg]][[Image:global.jpg]][[Image:giga.jpg]] | |||
(a) Three-dimensional Torus. (b) Global Collective Network. (c) IBM BG/L Control Network & Gigabit Ethernet networks | |||
Source [http://www.research.ibm.com/journal/rd/492/gara.pdf IBM BG/L] | |||
''IBM Blue Gene employs simultaneous send/receive technique in the torus network. Hence if there are N numbers of nodes, then a single node can send/receive with 2N other nodes simultaneously along its 2N different links.'' | |||
[[Image:torus.jpg]] | |||
''If the cost of a single send is given by Ts (without simultaneous send) then for ‘S’ simultaneous sends the total cost becomes'' | |||
<center>Ts + Ts x (S – 1) x f where f: 0 < f < 1 </center> | |||
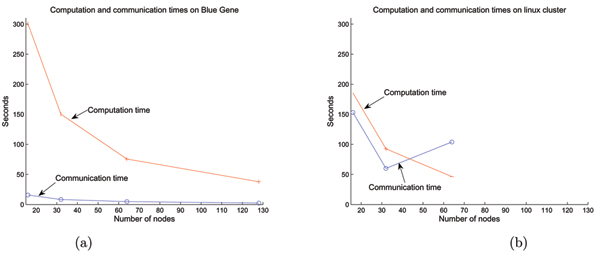
''The speedup is 1/f approximately. Below is the performance comparison of an algorithm (used for image processing in microscopy application) running on Blue Gene/L versus an Intel Linux cluster which does not employs simultaneous send.'' | |||
[[Image:bll.jpg]] | |||
*source: [http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=1924514 BMC Cell Biology] | |||
''For Linux Cluster the computation time is very high percentage (up to 40%) of the total time. In Blue Gene it is as less as 5% of total runtime.'' | |||
From processor’s point of view there are number of other network delays which can be categorized as occupancy. Contention for resources can be viewed as one of the occupancies. The net bandwidth reduces as a result of this. If P concurrent processors are using a network of Bandwidth B, then the effective bandwidth would be B/P. Contention are basically two types. When it is due to routers and switches it is called network contention. If it is observed at endpoints or processing nodes it is called endpoint contention. When the contention of endpoint type occurs, then all the processing nodes involved are called hot spot. This type of contention can easily alleviate in software. | |||
''The global interrupt and barrier network and global tree network operate in parallel which provides global asynchronous sideband signals. This basically results in lower roundtrip latency, as low as 1.3micro seconds. Network contention can always increase the latency. IBM BG/L uses Virtual cut through (VCT) routing technique.'' | |||
==== Communication Cost ==== | |||
At the end of the day we want to reduce the communication cost. Communication cost is given by following equation: | |||
<tt><center>'''Communication cost = Frequency of communication x (Communication Time – Overlap)'''</center></tt> | |||
Frequency of communication is self explanatory, which depends on the machine architecture and program design. Some architecture like scale-up symmetric multiprocessing (SMP) and scale-out massively parallel processing (MPP) [http://www.microsoft.com/technet/solutionaccelerators/cits/interopmigration/unix/hpcunxwn/ch01hpc.mspx (Microsoft Solution: HPC)] systems supports tightly coupled parallel applications. This result in high frequency of communication, which makes it important to have the other parts of communication time like overhead and network delays to be small. Loosely coupled parallel applications, on inherently parallel system architecture, requires minimal inter process communication. | |||
The portion of the communication operation which is performed concurrently with processor engaged in other useful work (computation and other communication) is the overlap. This concept is exploited to obtain high throughput. For instance, each node of IBM BG/L has IBM CMOS ASIC. Each of this ASIC has two independent cores (microprocessor). Virtually there is no difference in the core, each processor can handle its own communication or one processor can be used for communication and another for computation. This way very high degree of overlap is achieved. | |||
=== Scalability === | |||
Scalability of parallel computer is so important performance metrics that it was worth giving a heading for this. A general perception is that by increasing the number of processors arbitrarily, performance increases. This is not absolutely true while calculating parallel computer performance. Scalability means there exist an isoefficiency function for a parallel system such that upon increasing the size of problem the efficiency remains same. Scalability is bounded by two different limits. Weak scaling- when the load on individual processor remains same but the number of processor is increased. Strong Scaling- the problem size remaining same but load on individual processor is reduced while increasing the processor count. Generally all problem lies in between these two limits. | |||
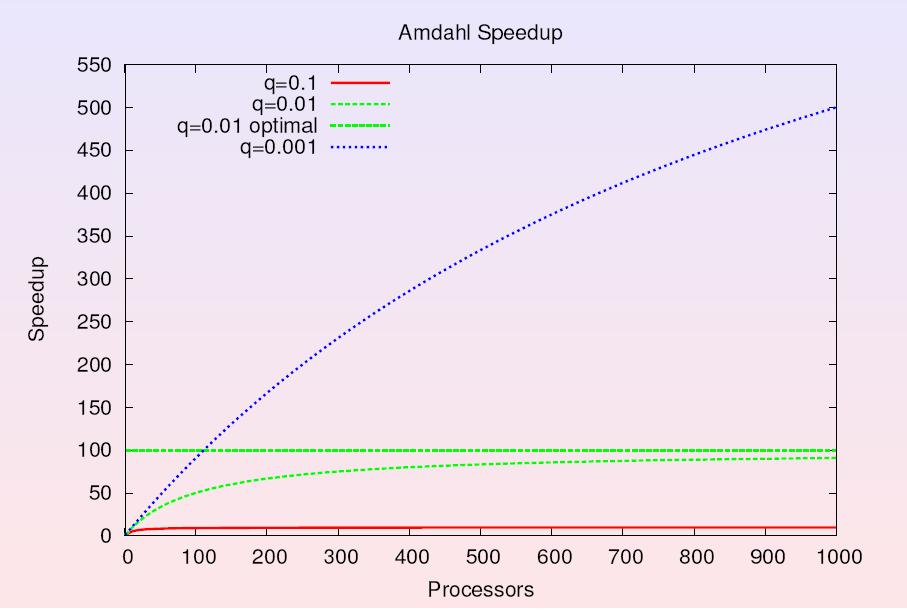
Is there a limit to the number of processor? Amdahl's law gives a picture of how performance is affected by increasing the number of processor. If a problem size is fixed and if it takes execution time T in the uni-processor system then on parallel system with P processors it will take | |||
<center>T x q + (1 – q) x T / P</center> | |||
Where T x q is time taken by sequential part of the program. Then the speed up is | |||
<center>S = 1 / (q + (1 – q)/P)</center> | |||
This upon simulating gives following result | |||
[[Image:amdhals.jpg]] | |||
Source: Lecture Notes: [http://hal.iwr.uni-heidelberg.de/lehre/pcc-05/lecture5.pdf Course on Parallel Computing by Peter Bastian] | |||
It can be concluded from the graph that not necessarily all algorithms will produce high speedups. It depends what we running. Scalability is thus dependent on the application, and hence while scaling up a system the application area needs to be specified. | |||
== Bibiliography == | |||
1.[http://www.amazon.com/Parallel-Computer-Architecture-Hardware-Software/dp/1558603433 Parallel Computer Architecture: A Hardware/Software Approach by David Culler and J.P. Singh with Anoop Gupta ] | |||
2.[http://www.amazon.com/Computer-Architecture-Fourth-Quantitative-Approach/dp/0123704901 Computer Architecture, Fourth Edition: A Quantitative Approach by John L. Hennessy , David A. Patterson] | |||
3.[http://www.cs.princeton.edu/~jps/ Parallel Computer Architecture Lecture notes By Jaswinder Pal Singh] | |||
4.[http://www.microsoft.com/technet/solutionaccelerators/cits/interopmigration/unix/hpcunxwn/ch01hpc.mspx Microsoft Solution: High Performance Computing] | |||
5.Lecture Notes: [http://hal.iwr.uni-heidelberg.de/lehre/pcc-05/lecture5.pdf Course on Parallel Computing by Peter Bastian] | |||
6.[http://www.research.ibm.com/journal/rd/492/gara.html IBM Blue Gene/L] | |||
Latest revision as of 03:59, 11 September 2007
Sections 1.3.3 and 1.3.4: Most changes here are probably related to performance metrics. Cite other models for measuring artifacts such as data-transfer time, overhead, occupancy, and communication cost. Focus on the models that are most useful in practice.
Communication and Replication
In this section, we describe two terms Communication and Replication, simultaneously we also make distinction between these two terms.
Communication between any two processes is said to occur when data written by one process is read by second process. This causes a data transfer between the processes however, if data is just stored at one process (because initially data was configured to be on this process or it was too large to fit at any other place) and transfer only makes another copy of the data at second process then it called replication. For example, on processor’s request of data if we copy something from main memory and put it in cache this operation is replication of data. On the contrast if a data is produced by a sender process and it is transferred to a receiver process by message passing then it is an example of communication.
Communication and replication both involves data transfer, which can be defined as transfer of data across different memory locations. For interprocess(or) communication the data is transferred across the memory local to the communicating processor or from a remote storage device. When a miss occurs in cache, the data is transferred from the memory to the cache. In case, where the cache content, as a result of replication, is updated or changed, these changes must be transported to all the other hidden replicas. This is another aspect of data transfer.
Performance
Introduction
In this section, we briefly discuss various importance aspects of performance measurement in parallel computer architecture and basic performance metrics.
As we already know, performance measurement is one of the fundamental issues in uniprocessor system where architects focus on improving performance by reducing execution time of standard programs called benchmarks. They use several techniques such as minimizing memory access time, designing hardware which can execute many instruction in parallel and possibly faster (micro level parallelism extraction) etc. Performance measurement is more serious concern in parallel computing because apart from computing performance measurement we also need to analyze communication cost as data is shared among many processors and processes (possibly on different processors) need to communicate efficiently, coherently and correctly.
To make our point more precise, let us consider the following example:
- Assume we want to run a program which takes 100sec on uniprocessor. However, we also know that the full program can be decomposed in many processes and these processes can be run on different machine. So basically, in best case we expect the speed up of n where n is the number of processors available. We have divided the computing load but these processes can not run independently to achieve the completion. To run the program correctly, these processes do need to communicate to each other for data sharing, synchronization etc. Hence, there is communication overhead involved in parallel computing.
Following figure (reference) helps in understanding how parallel processers typically spend their execution time on different activities like: local/remote data access, computing, synchronization and other work.
A sequential program takes 100 sec to run the program, in this hypothetical example it is assumed that 80% time is busy-useful (i.e.execution of instructions) time however rest 20% of the time processor spends in accessing local data. Four parallel processors solve the same problem in 55 seconds (speed up of 1.8 instead of expected speed up of 4). Parallel processors spend time in accessing data at both locations : remote and local. These processors execute instructions which we call busy useful time and moreover they synchronize with each other to execute the program correctly. However in such a parallel computing environment, processors execute some instructions/work which are not needed if program is run sequentially, time spent in such activities is called busy-overhead time. Such type of work is also called 'extra work' which we will discuss shortly.
Clearly, a wise architect would not like to have any parallel system where communication overheads overwhelm speed up achieved by dividing the computing-load. In other words, diving computing load on different processors is good idea only when communication costs do not shoot up too much. Similarly, in order to reduce communication cost one should not kill the inherent parallelism available in the program.
Speedup (reference) gain by parallel computing has to take into the account the synchronization time, communication cost and extra work apart from computing work. So, speed up can be expressed as following:
In the equation above, 'extra work' is work done by processors other than computation, synchronization and communication. This might include:
- Computing a good partition for a particular problem.
- Using redundant computation to avoid communication.
- Task, data and process management overhead etc.
Hence, it is obvious that in order to increase the speed up (improve performance), architects would focus on all the factors appearing in the denominator of above equation. Therefore, we need to consider various design trade-offs while analyzing performance of parallel computing architecture.
There are three basic performance metrics.
- Latency : Time taken by an operation to get completed. ( measured as seconds per operation)
- Bandwidth: The rate at which operations are executed. (measured as operations per second)
- Cost: Cost is basically impact of operations on total execution time of the program. (measured as latency times number of operations)
In uniprocessor system, bandwidth is simply reciprocal of latency however, in parallel computing many operations are performed concurrently so relationship among performance metrics is not simple.In parallel computing, we need to consider the performance for communication operations along with computing operations.
We list three artifacts of measuring performance and since data transfer operations are the most frequent type of communication operation, discussion on the same appears first.
Artifacts of Measuring Performance
Data Transfer
For any data transfer we would like to estimate the time it consumes, so that we can improve the overall performance of the system by reducing data transfer time. To estimate the data transfer time a simple linear model is used ( referenced lecture material):
Total transfer time has two components: 1. A constant term (T0) which is called start up cost. We will shortly return to this with more details. 2. Data transfer time, which is estimated as following:
Bandwidth (B) is also called data transfer rate.
To have better understanding of the model, we should be clear about the following points:
- If we have only one pair of host then data transfer rate is simply the bandwidth of the link connecting those hosts.
- However if there are many hosts between the source host and destination host, bottleneck is the link with lowest bandwidth.
Important point to note is that the achievable bandwidth depends on the transfer size, that is why sometimes bandwidth (B) is called as peak bandwidth. For example:
- Suppose we have two hosts connected by a link with bandwidth of 20MB/s and start up cost of communication is 2 micro seconds. We want to transfer an image of size 40MB then the total transfer time is 2 seconds plus 2 micro seconds. Given the available peak bandwidth of 20MB/s, one might have expected to complete the transfer in 2 seconds achieving the peak bandwidth but start up cost prohibits this. Clearly as you increase the amount of data achievable bandwidth approaches the asymptotic rate of bandwidth (B), in fact start up cost determines how fast the asymptotic rate would be achieved.
As a special case, the amount of data required to achieve half of peak bandwidth (B) is equal to T0 X B. This is also called half-power point. Please note that printed version of the text-book has erroneous formula for calculating half-power point.
Now, we discuss first part of total transfer-time i.e. start-up cost. Notice that T0 is a constant term for a particular data transfer,but it might vary as we consider data transfer over different entities. For example, in memory operation start up cost is memory access time. In message passing the start up cost can be estimated as time taken by fist bit to reach destination. For pipelined operations, start up cost is simply time taken to fill up the pipeline. For bus transactions it is arbitration and command phases.
As parallel computing has advanced, one of the major focuses has been to reduce start up cost. There are many ways to do so; we describe few of them here. As stated earlier start up cost for memory operations is basically the memory access time. To reduce memory access time, architects have introduced costly (hence small size) but fast storage area called cache. Depending upon the spatial and temporal locality cache is filled with useful items and hence processor does not have to go to memory (long latency ) every time it needs data. Average access time is governed by the following formula Computer Architecture: A Quantitative Approach, Appendix C:
Therefore architects often try to reduce all three components by adopting different cache optimization like: multilevel cache, larger blocks size, higher associatively etc.
We quote the access time of cache and main memory to see how beneficial it might be to introduce cache if we manage to get considerably high hit rates. Cache access time is typically 0.5-25 ns while for the main memory it is 50-250 ns, so we can decrease start-up cost considerably by having such a memory hierarchy. Bandwidth for caches range around 5,000-20,000 MB/sec but for memory its as low as 2,500-10,000MB/sec. Computer Architecture: A Quantitative Approach, Appendix C
Similarly for bus transactions, start up cost is time spent during arbitration and command phases, suppose on a 3.6 GHz Intel Xeon machine (year 2004) it takes 3 cycles to arbitrate the bus and present the address the start up cost is around 0.83 nano seconds. However assuming that around year 1994-95 it took same 3 cycles on Alpha 21064A 0.3 GHz processor we can see that start up cost has been reduced by more than 10 times. Computer Architecture: A Quantitative Approach, Chapter 1
Pipelining is another way to reduce the data transfer time, for pipelined systems filling up the pipeline is the total start up cost. Though it seems that introducing pipeline adds extra start up cost, however more importantly pipeline allows multiple operations to take place concurrently and this indeed helps in achieving higher bandwidth.Computer Architecture: A Quantitative Approach, Appendix A
Startup cost calculation is many times challenging, with enhancement in technology focus is too reduce the start-up cost and increase bandwidth.
Next plot (on log-log scale) shows time for message passing operation for several machines as a function of message size source. We notice the start-up costs for different machines vary a lot (nearly spread over an order of magnitude). These start up costs vary a lot and total transfer size is non linear function of message size for small amount of data, contrary to linear data transfer model. For big size data transfer we get almost linear relationship. The bandwidth can be calculated by slope of the line.
Quoting other figures,
iPSC/2 machine has start up cost of 700 micro seconds and CRAY T3D (PVM) machine has start up cost of 21 micro seconds, we can clearly see the trends that within one decade start up cost has dropped by an order of magnitude. NOW machine has start up cost of just 16 micro seconds. Basically these improvements are essentially due to improvement in cycle time.
Similar trends can be observed in 'Maximum Bandwidth' achievable on each machine for data transfer. For nCUBE/2 machine maximum bandwidth was 2 MB/s but relatively advanced machines like SP2 has bandwidth of 40 MB/s.
- However, this data transfer model has few shortcomings too.
This model does not indicate when the next operation can be performed. Estimating time interval between two operations is particularly very useful because bandwidth depends on how frequently operations can be initiated. This model also does not tell about whether other useful work can be done during transfer or not. This model is easy to understand but it is not very suitable for architectural evaluation. For network transactions, total message time is difficult to measure unless there is a global clock as the send and receive usually happen on different processors.So, transaction time is usually measured by doing a echo test (i.e. one processor sends the data and waits until it receives a message). But this is reliable only if receive is posted before message arrives hence measuring transaction time is very challenging (and not always accurate) in this transfer model.
- In this section we discussed different aspects of data transfer model.In parallel computing environment, data transfers usually take place across the network and it is invoked by processor through the communication assist. Therefore, now we need to look at how communication costs are estimated and what are the important factors to consider?
Overhead and Occupancy
One of the three components of Processor execution time, apart from Computation Time and Idle Time, is Communication Time. Communication time is the time spent by the processor on exchanging messages with another process(or). There can be two different types of communication, i.e. interprocessor and intraprocessor. In interprocessor communication the two communicating tasks are handled by two different processors. While in intraprocessor communication the communicating tasks are handled by the same processor. Generally both intraprocessor and interprocessor communication costs the same, provided the former is not highly optimized.
Communication time is function of number of bytes (n) transferred across. It can be given as below
Source Lecture :Culler
Communication Overhead includes time spent on
- Create messages
- Execute communications protocols
- Physically send messages
- Run through the protocol sets and decode the message on the receiving node.
During this period the processor cannot do any useful or computational work. Parallel programs, running on different processors need to coordinate their work among themselves. This results in increased rate of interprocessor communication, which in turn increases the net overhead cost.
Occupancy is the time spent at the slowest component in the communication assist and it affects performance in couple of ways. It delays the current request and indirectly contributes to the delays of subsequent requests. The occupancy gets to set the upper limit on how frequently communication operation can be initiated by the processor.
Some of the recent trends/designs helped reduce these communication costs. IBM Blue Gene (L) uses Global Collective Network, which carries out operations within the network itself. This saves the processors time to decode messages with intermediate values, calculate new intermediate values, create new messages, and send them on to other nodes. The overhead now is primarily because of communication protocol. It also has a dedicated communications network, Global Barrier and Interrupt Network, to speed up task-to-task coordination activities. IBM BG/L also employs Torus Network, which results in linear growth of the path length while nodes (processors) scale as a cube. Torus Network also gives the ability to send messages in either direction, something like a ring network and hence reduces the distance between furthest points to half. This in turn reduces the network delays.
(a) Three-dimensional Torus. (b) Global Collective Network. (c) IBM BG/L Control Network & Gigabit Ethernet networks
Source IBM BG/L
IBM Blue Gene employs simultaneous send/receive technique in the torus network. Hence if there are N numbers of nodes, then a single node can send/receive with 2N other nodes simultaneously along its 2N different links.
If the cost of a single send is given by Ts (without simultaneous send) then for ‘S’ simultaneous sends the total cost becomes
The speedup is 1/f approximately. Below is the performance comparison of an algorithm (used for image processing in microscopy application) running on Blue Gene/L versus an Intel Linux cluster which does not employs simultaneous send.
- source: BMC Cell Biology
For Linux Cluster the computation time is very high percentage (up to 40%) of the total time. In Blue Gene it is as less as 5% of total runtime.
From processor’s point of view there are number of other network delays which can be categorized as occupancy. Contention for resources can be viewed as one of the occupancies. The net bandwidth reduces as a result of this. If P concurrent processors are using a network of Bandwidth B, then the effective bandwidth would be B/P. Contention are basically two types. When it is due to routers and switches it is called network contention. If it is observed at endpoints or processing nodes it is called endpoint contention. When the contention of endpoint type occurs, then all the processing nodes involved are called hot spot. This type of contention can easily alleviate in software.
The global interrupt and barrier network and global tree network operate in parallel which provides global asynchronous sideband signals. This basically results in lower roundtrip latency, as low as 1.3micro seconds. Network contention can always increase the latency. IBM BG/L uses Virtual cut through (VCT) routing technique.
Communication Cost
At the end of the day we want to reduce the communication cost. Communication cost is given by following equation:
Frequency of communication is self explanatory, which depends on the machine architecture and program design. Some architecture like scale-up symmetric multiprocessing (SMP) and scale-out massively parallel processing (MPP) (Microsoft Solution: HPC) systems supports tightly coupled parallel applications. This result in high frequency of communication, which makes it important to have the other parts of communication time like overhead and network delays to be small. Loosely coupled parallel applications, on inherently parallel system architecture, requires minimal inter process communication.
The portion of the communication operation which is performed concurrently with processor engaged in other useful work (computation and other communication) is the overlap. This concept is exploited to obtain high throughput. For instance, each node of IBM BG/L has IBM CMOS ASIC. Each of this ASIC has two independent cores (microprocessor). Virtually there is no difference in the core, each processor can handle its own communication or one processor can be used for communication and another for computation. This way very high degree of overlap is achieved.
Scalability
Scalability of parallel computer is so important performance metrics that it was worth giving a heading for this. A general perception is that by increasing the number of processors arbitrarily, performance increases. This is not absolutely true while calculating parallel computer performance. Scalability means there exist an isoefficiency function for a parallel system such that upon increasing the size of problem the efficiency remains same. Scalability is bounded by two different limits. Weak scaling- when the load on individual processor remains same but the number of processor is increased. Strong Scaling- the problem size remaining same but load on individual processor is reduced while increasing the processor count. Generally all problem lies in between these two limits.
Is there a limit to the number of processor? Amdahl's law gives a picture of how performance is affected by increasing the number of processor. If a problem size is fixed and if it takes execution time T in the uni-processor system then on parallel system with P processors it will take
Where T x q is time taken by sequential part of the program. Then the speed up is
This upon simulating gives following result
Source: Lecture Notes: Course on Parallel Computing by Peter Bastian
It can be concluded from the graph that not necessarily all algorithms will produce high speedups. It depends what we running. Scalability is thus dependent on the application, and hence while scaling up a system the application area needs to be specified.
Bibiliography
3.Parallel Computer Architecture Lecture notes By Jaswinder Pal Singh
4.Microsoft Solution: High Performance Computing
5.Lecture Notes: Course on Parallel Computing by Peter Bastian