CSC/ECE 517 Fall 2020 - E2078. Improve self-review Link peer review & self-review to derive grades: Difference between revisions
| (58 intermediate revisions by 3 users not shown) | |||
| Line 30: | Line 30: | ||
=== Files Involved === | === Files Involved === | ||
== Tasks == | '''Back-end''' | ||
*app/controllers/grades_controller.rb | |||
*app/helpers/grades_helper.rb | |||
*app/models/assignment_participant.rb | |||
*app/models/author_feedback_questionnaire.rb | |||
*app/models/response_map.rb | |||
*app/models/review_questionnaire.rb | |||
*app/models/self_review_response_map.rb | |||
*app/models/teammate_review_questionnaire.rb | |||
*app/models/vm_question_response.rb | |||
'''Front-end''' | |||
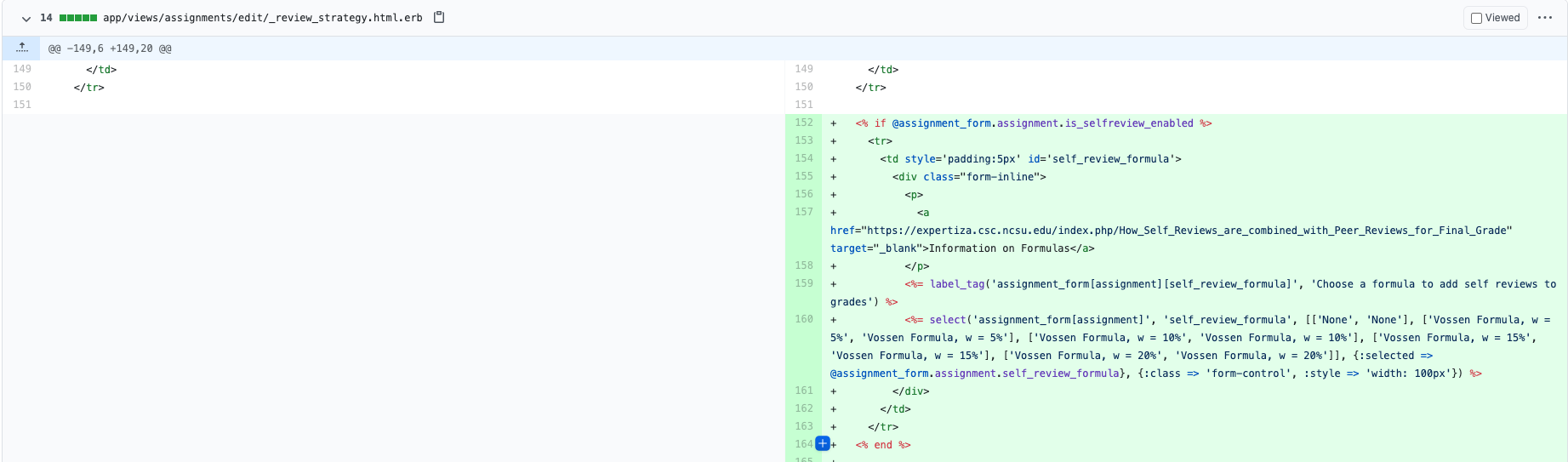
*app/views/assignments/edit/_review_strategy.html.erb | |||
*app/views/grades/_participant.html.erb | |||
*app/views/grades/_participant_charts.html.erb | |||
*app/views/grades/_participant_title.html.erb | |||
*app/views/grades/view_team.html.erb | |||
'''Testing''' | |||
*spec/models/assignment_particpant_spec.rb | |||
*spec/controllers/grades_controller_spec.rb | |||
=== Use Case for Self-Assessment === | |||
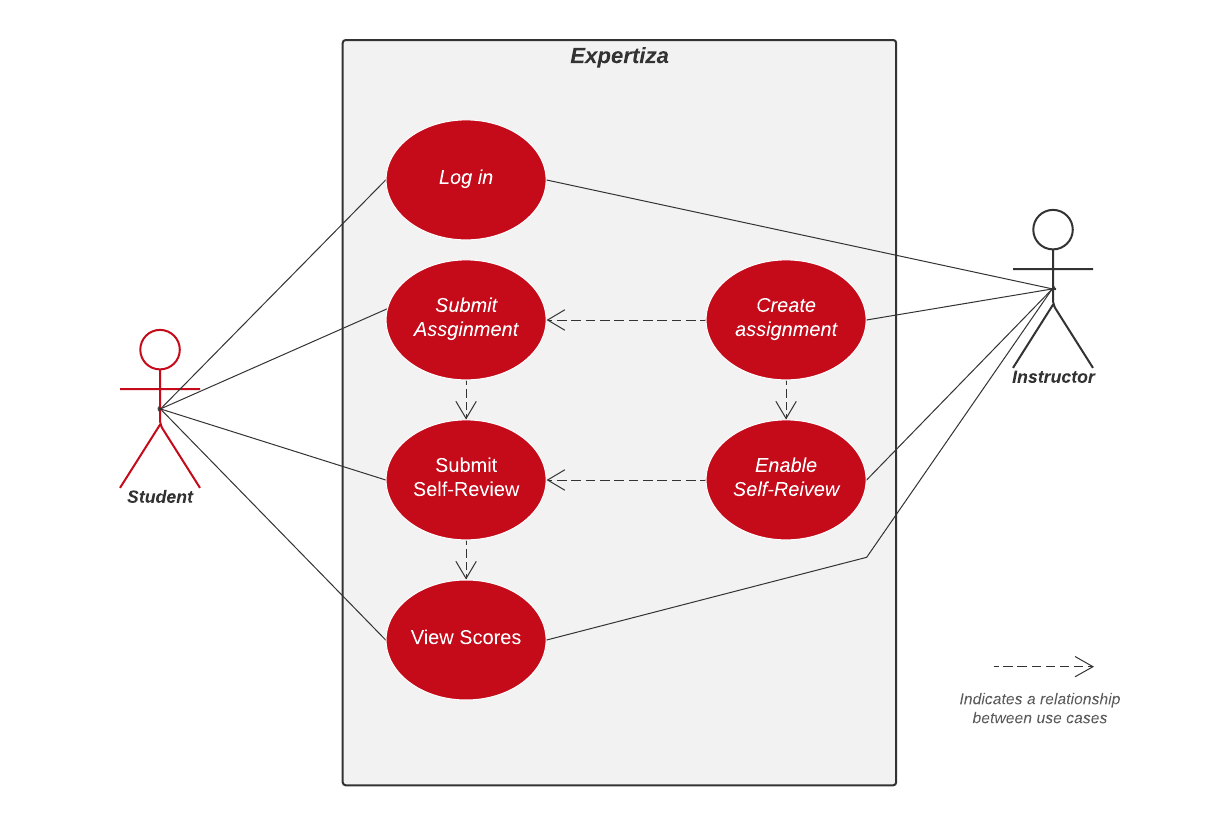
The following diagram illustrates how the self-assessment feature should work between student and instructor within Expertiza. In summary, an instructor can create an assignment and enable self-review. A student can then submit to the assignment creates by the instructor and provide a self-review. Only then can the student view all of their review scores. | |||
[[File:Use case diagram e2078.png|750px]] | |||
== Design Plan for Tasks == | |||
=== Display Self-Review Scores w/ Peer-Reviews === | === Display Self-Review Scores w/ Peer-Reviews === | ||
| Line 36: | Line 67: | ||
It should be possible to see self-review scores juxtaposed with peer-review scores. Design a way to show them in the regular "View Scores" page and the alternate (heat-map) view. They should be shown amidst the other reviews, but in a way that highlights them as being a different kind of review. | It should be possible to see self-review scores juxtaposed with peer-review scores. Design a way to show them in the regular "View Scores" page and the alternate (heat-map) view. They should be shown amidst the other reviews, but in a way that highlights them as being a different kind of review. | ||
==== Design Plan ==== | |||
In the current implementation of Expertiza, students can view a compilation of all peer review scores for each review question and an average of those peer-reviews. For our project, we plan to add the self-review score alongside the peer-review scores for each review question. In the wire-frame below, note that for each criterion there is a column for each peer-review score and a single column for the self-review score. | In the current implementation of Expertiza, students can view a compilation of all peer review scores for each review question and an average of those peer-reviews. For our project, we plan to add the self-review score alongside the peer-review scores for each review question. In the wire-frame below, note that for each criterion there is a column for each peer-review score and a single column for the self-review score. Currently implemented in the system, the avg column takes an average of all the review scores. These scores (peer-reviews average and self-review) will be used to determine the overall composite score for the team's reviews. Furthermore, the average composite score is displayed on the page under the average peer review score, labeled "Final Average Peer Review Score". How we plan to derive a composite score is explained in detail in the follow section [https://expertiza.csc.ncsu.edu/index.php/CSC/ECE_517_Fall_2020_-_E2078._Improve_self-review_Link_peer_review_%26_self-review_to_derive_grades#Derive_Composite_Score Derive Composite Score]. | ||
[[File:View wireframe.png|700px]] | [[File:View wireframe v3.png|700px]] | ||
In the alternate view, our plan does not alter the current interface too much. The only addition we plan to implement is | In the alternate view, our plan does not alter the current interface too much. The only addition we plan to implement is additional columns for the self-review average and for the composite (final) score a student has received for an assignment. Likewise, there is now an additional doughnut chart providing a visual of the composite score (green) alongside the final review score (yellow). | ||
[[File:Alternate view wireframe v3.png|1150px]] | |||
''Note: The diagrams above are wireframes. The values displayed are not be taken literally, they are for design purposes only.'' | |||
=== Derive Composite Score === | === Derive Composite Score === | ||
| Line 52: | Line 83: | ||
Implement a way to combine self-review and peer-review scores to derive a composite score. The basic idea is that the authors get more points as their self-reviews get closer to the scores given by the peer reviewers. So the function should take the scores given by peers to a particular rubric criterion and the score given by the user. The result of the formula should be displayed in a conspicuous page on the score view. | Implement a way to combine self-review and peer-review scores to derive a composite score. The basic idea is that the authors get more points as their self-reviews get closer to the scores given by the peer reviewers. So the function should take the scores given by peers to a particular rubric criterion and the score given by the user. The result of the formula should be displayed in a conspicuous page on the score view. | ||
The formula we use to determine a final grade from, 1) the peer reviews and 2) how closely self reviews match the peer reviews, uses a type of additive scoring rule, which computes a weighted average between team score (peer reviews) and student rating (self review). More specifically, it uses a type of mixed additive-multiplicative scoring rule, which multiplies student score (self review) by a function of the team score (peer reviews), and adds its weighted version to the weighted peer review score. This is also known as 'assessment by adjustment'. The formula is a practical scoring rule for additive scoring with unsigned percentages (grades from 0%-100%). | The formula we use to determine a final grade from, 1) the peer reviews and 2) how closely self reviews match the peer reviews, uses a type of additive scoring rule, which computes a weighted average between team score (peer reviews) and student rating (self review). More specifically, it uses a type of mixed additive-multiplicative scoring rule, which multiplies student score (self review) by a function of the team score (peer reviews), and adds its weighted version to the weighted peer review score. This is also known as 'assessment by adjustment'. The formula is a practical scoring rule for additive scoring with unsigned percentages (grades from 0%-100%). | ||
The pseudo-code for a function that implements the formula is as | The pseudo-code for a function that implements the formula is as follows: | ||
function(avg_peer_rev_score, self_rev_score, w) | function(avg_peer_rev_score, self_rev_score, w) | ||
grade = w*(avg_peer_rev_score) + (1-w)*(SELF) | grade = w*(avg_peer_rev_score) + (1-w)*(SELF) | ||
| Line 64: | Line 93: | ||
SELF = avg_peer_review_score * (1 - (|avg_peer_review_score - self_review_score|/avg_peer_review_score)) | SELF = avg_peer_review_score * (1 - (|avg_peer_review_score - self_review_score|/avg_peer_review_score)) | ||
and where: | and where: | ||
avg_peer_review_score is simply the mechanism already existing in Expertiza for assigning a grade from peer review scores. | |||
and where: | and where: | ||
w - weight - (0 <= w <= 1) is the inverse proportion of how much of the final grade is determined by the closeness of the self review to the average of the peer reviews (w is the proportion of the grade to be determined by the original grade determination: the peer review scores). | |||
An example: | An example: | ||
* average peer review score is 4/5, self review score is 5/5 | * The average peer review score is 4/5, the self review score is 5/5. | ||
* | * The instructor chooses w to equal 0.95, so that 5% of the grade is determined from the deviation of the self review from the peer reviews. | ||
The final grade, instead of being the peer review score of 4 | The final grade, instead of being the peer review score of 4/5 ('''80%''') is now: | ||
0.95*(4/5) + 0.05*(4/5*(1-|4/5-5/5|/(4/5))) = 79% | 0.95*(4/5) + 0.05*(4/5*(1-|4/5-5/5|/(4/5))) = '''79%'''. | ||
If the instructor chose w to equal 0.85 (instead of 0.95), the grade is 77% (instead of 79%) because deviation from peer reviews is a larger weighted value of the final grade. | If the instructor chose w to equal 0.85 (instead of 0.95), the grade is '''77%''' (instead of 79%) because deviation from peer reviews is a larger weighted value of the final grade. | ||
The above is a basic version of the grading formula. It is basic in that it only allows deviations of the self review scores from the peer review scores to result in a decrease in the final grade ''and'' a deviation will ''always'' result in a decrease of the final grade. We propose another parameter to the formula, l - leniency | The above is a basic version of the grading formula. It is basic in that it only allows deviations of the self review scores from the peer review scores to result in a decrease in the final grade ''and'' a deviation will ''always'' result in a decrease of the final grade. We propose another parameter to the formula, l - leniency, as another way (in addition to w - weight) for the instructor to modularly determine the final grade for an assignment. The parameter l - leniency - can determine a threshold by which the final grade will account/adjust for self reviews' deviations from peer reviews only when the deviation reaches this threshold (measured in percentage deviation from the average peer review). If the difference does not meet the threshold, no penalty will be subtracted from the peer review. In addition, if the difference does not meet the threshold (the self review score is sufficiently close to the peer review scores), the instructor can choose to add points to final grade based on the magnitude of the difference. Since the formula is a mixed additive-multiplicative scoring rule (mentioned above), the instructor needs to simply pick l - leniency - as a percentage (similar to the functionality of w). | ||
To recap: w should be chosen based on the instructor's desired percentage (w) ''of the final grade'' to be determined from peer reviews and, conversely, the instructor's desired percentage (1-w) ''of the final grade'' to be determined by the extent to which self reviews deviate from peer reviews. In addition, l - leniency, should be chosen based on the instructor's desired percentage ''of the deviation of self review from peer review'' that could result in no grade deduction from the deviation if the deviation is sufficiently small (or even a grade increase if the instructor wants to increase the score of individuals with a small deviation). | |||
function(avg_peer_rev_score, self_rev_score, w) | The following is pseudo-code for if an instructor wishes to not subtract from the final grade if the deviation is sufficiently small. Notice that the leniency condition, the instructor's desired percentage ''of the deviation of self review from peer review'', is naturally part of the grading formula in SELF: | ||
if |avg_peer_review_score - self_review_score|/avg_peer_review_score <= l(leniency) | |||
grade = avg_peer_review_score | |||
else | |||
run formula | |||
In addition. instead of assigning a final grade equal to the avg_peer_review_score if the leniency condition is met, the grade can be adjusted (increased) if the instructor wishes to do so, since the self review is sufficiently close (determined by l) to the peer reviews. The formula for determining the final grade would thus add the small extent of deviation to the final grade rather than subtracting it (in SELF, 1 - ..., is changed to 1 + ...): | |||
function(avg_peer_rev_score, self_rev_score, w) | |||
grade = w*(avg_peer_rev_score) + (1-w)*(SELF) | |||
where SELF = avg_peer_review_score * (1 + (|avg_peer_review_score - self_review_score|/avg_peer_review_score)) | where: | ||
SELF = avg_peer_review_score * (1 '''+''' (|avg_peer_review_score - self_review_score|/avg_peer_review_score)) | |||
In this case, the pseudo-code is: | |||
if |avg_peer_review_score - self_review_score|/avg_peer_review_score <= l(leniency) | |||
grade = w*(avg_peer_rev_score) + (1-w)*(avg_peer_review_score * (1 '''+''' (|avg_peer_review_score - self_review_score|/avg_peer_review_score))) | |||
else | |||
grade = w*(avg_peer_rev_score) + (1-w)*(avg_peer_review_score * (1 '''-''' (|avg_peer_review_score - self_review_score|/avg_peer_review_score))) | |||
Using the previous example (average peer review score is 4/5, self review score is 5/5, w = 0.95), the self review score (5/5) differs by 25% of the peer review score (4/5). In other words, |avg_peer_review_score - self_review_score|/avg_peer_review_score = 1/4 = 25%. Based on l - leniency, the instructor can decide: | |||
:1. if a 25% deviation is sufficiently large to warrant penalizing the final grade by (1-w)*(SELF) (so that the final grade is '''79%''', instead of 80%). | |||
:2. if a 25% deviation is sufficiently small to warrant keeping the final grade as grade = avg_peer_review_score, with no penalty for the deviation (so that the grade is '''80%''') | |||
:3. if a 25% deviation is sufficiently small to warrant increasing the final grade by (1-w)*(SELF), where the SELF formula contains a 1 + ..., instead of a 1 - ... (so that the grade is '''81%''') | |||
==== Implementation Plan ==== | |||
In order to incorporate the combined score into grading, we will change the logic in grades_controller.rb, which implements the grading formula. We will remove most of the code from the previous implementation since the formula/method used is unsatisfactory. '''With the new grading formula, the grades_controller can assign a final grade by following these steps:''' | |||
:1. We can obtain the peer review ratings and the score/grade derived from them by calling scores(), which then calls compute_assignment_score(), both from the assignment_participant.rb model. In order to compute the assignment score, compute_assignment_score() calls another method named get_assessments_for(), which is located in review_questionnare.rb model. | |||
:2. The get_assessments_for() method will call the reviews() method, also located in assignment_participant.rb. | |||
:3. Finally, the reviews() method will get the scores by simply calling the get_assessments_for() method located in the response_map.rb model. | |||
:4. Once the scores have been retrieved by using the various model methods, the controller can use the scores to calculated a final grade by using the formula. This grade is then passed to the view. | |||
Below is a flow diagram for how grades_controller.rb, which implements the grading formula (as mentioned in the first step) and presents the grade in the view (top of the diagram). Note: The self-review scores are obtained by using the true parameter in all the methods calls (as shown in the diagram), whereas the peer-review scores are retrieved similarly but omitting this parameter. | |||
[[File:E1926_code_flow.png]] | |||
=== Implement Requirement to Review Self before Viewing Peer Reviews === | === Implement Requirement to Review Self before Viewing Peer Reviews === | ||
| Line 122: | Line 168: | ||
There would be no challenge in giving the same self-review scores as the peer reviewers gave if the authors could see peer-review scores before they submitted their self-reviews. The user should be required to submit their self-evaluation(s) before seeing the results of their peer evaluations. | There would be no challenge in giving the same self-review scores as the peer reviewers gave if the authors could see peer-review scores before they submitted their self-reviews. The user should be required to submit their self-evaluation(s) before seeing the results of their peer evaluations. | ||
==== Implementation Plan ==== | |||
By being able to self review before peer review, it allows the author of the assignment to have an unbiased opinion on the quality of work they are submitting. When the judgement of their work is not influenced by others who have given feedback, they are able to get a clearer view of the strengths and weaknesses of their assignment. Self reviews before peer reviews can also be more beneficial to the user as it can show if the user has the correct or wrong approach to their solution compared to their peers. | |||
In the current implementation of self review, the user is able to see the peer reviews before they have made their own self review. The reason that this is occurring is due to the fact that when the user goes to see their scores, the page is not checking that a self review has been submitted. In order to fix this issue, we will add a boolean parameter to self review and pass it to viewing pages where it is called. When a user is at the student tasks view, the "Your scores" link will be disabled if the user has not filled out their self review. If the user has filled out their self review, then he/she will be redirected to the [https://expertiza.csc.ncsu.edu/index.php/CSC/ECE_517_Fall_2020_-_E2078._Improve_self-review_Link_peer_review_%26_self-review_to_derive_grades#Display_Self-Review_Scores_w.2F_Peer-Reviews Display Self-Review Scores with Peer-Reviews] page. | |||
Below is a control flow diagram for how a student will be able to view their peer and self review score. | |||
[[File:Control_Flow_SelfReview.png]] | |||
== Implementation of Design Plan == | |||
=== Display Self-Review Scores w/ Peer-Reviews === | |||
The following code and UI screenshots illustrate the implementation of displaying the self-review scores alongside the peer-reviews. This also includes displaying the final score that aggregates the self-review score utilizing a chosen formula. The final score derivation process is described in the [https://expertiza.csc.ncsu.edu/index.php/CSC/ECE_517_Fall_2020_-_E2078._Improve_self-review_Link_peer_review_%26_self-review_to_derive_grades#Derive_Composite_Score Derive Composite Score] task. | |||
'''View Team Review Scores (view_team)''' | |||
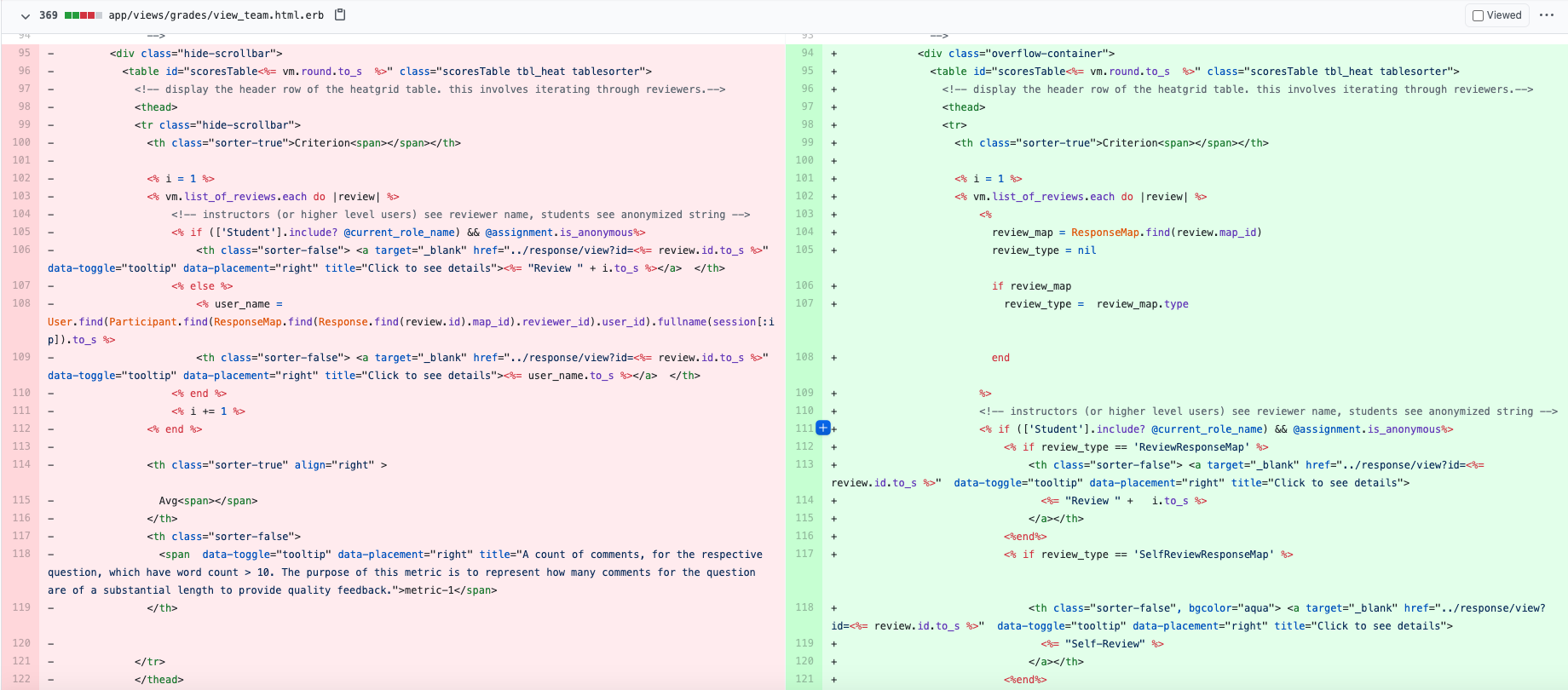
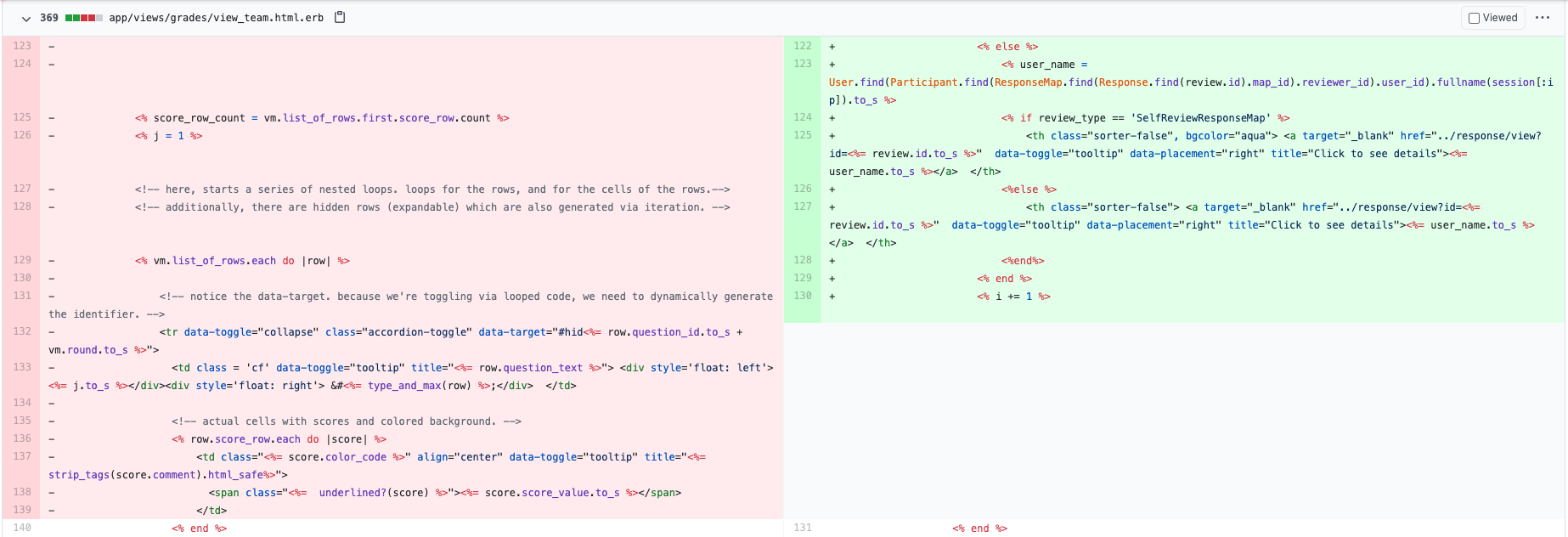
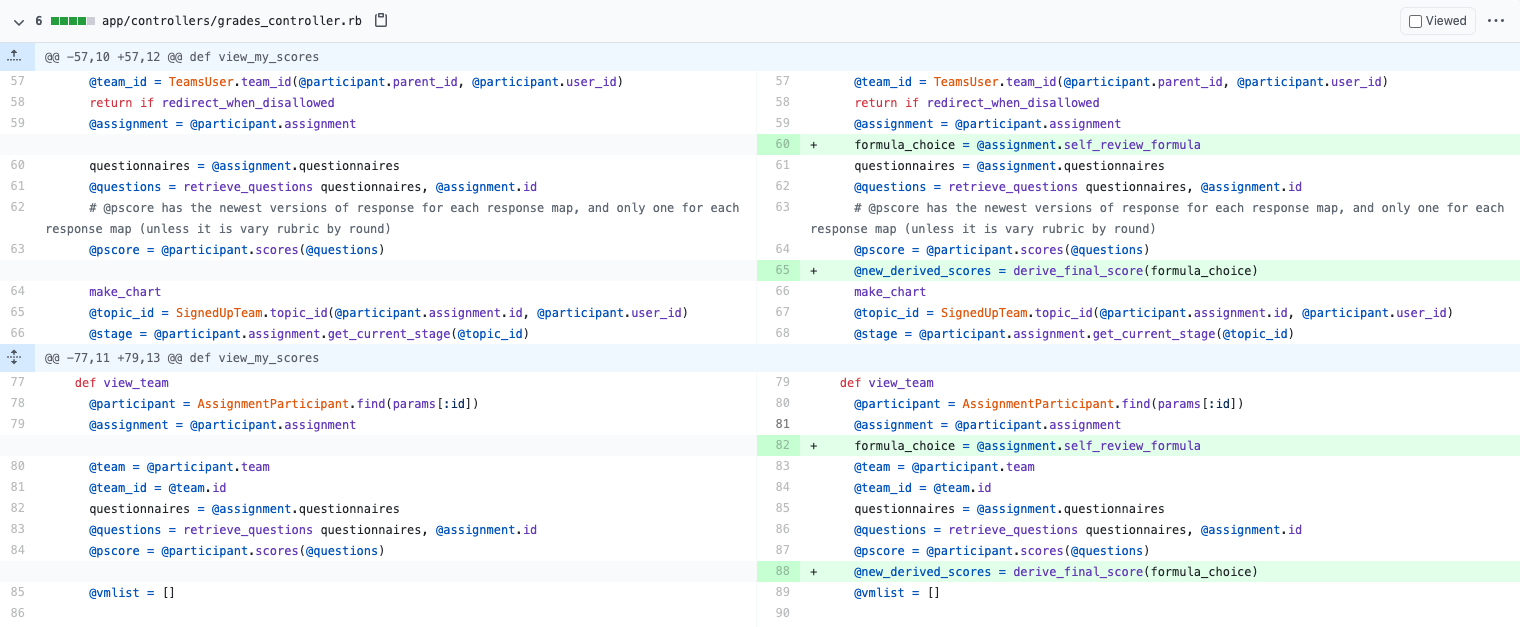
The view_team.html.erb file is responsible for the display of the peer-review scores heat map. In this implementation, we added a display for the Final Average Peer Review Score, which is the score that takes the average self-review score into consideration based on a set formula. Additionally, there is now a self-review score column (highlighted in cyan) that displays the self-review score for each criterion alongside the peer-review given. | |||
[[File:selfreviews16.png|1200px]] | |||
[[File:selfreviews17.png|1200px]] | |||
[[File:selfreviews18.png|1200px]] | |||
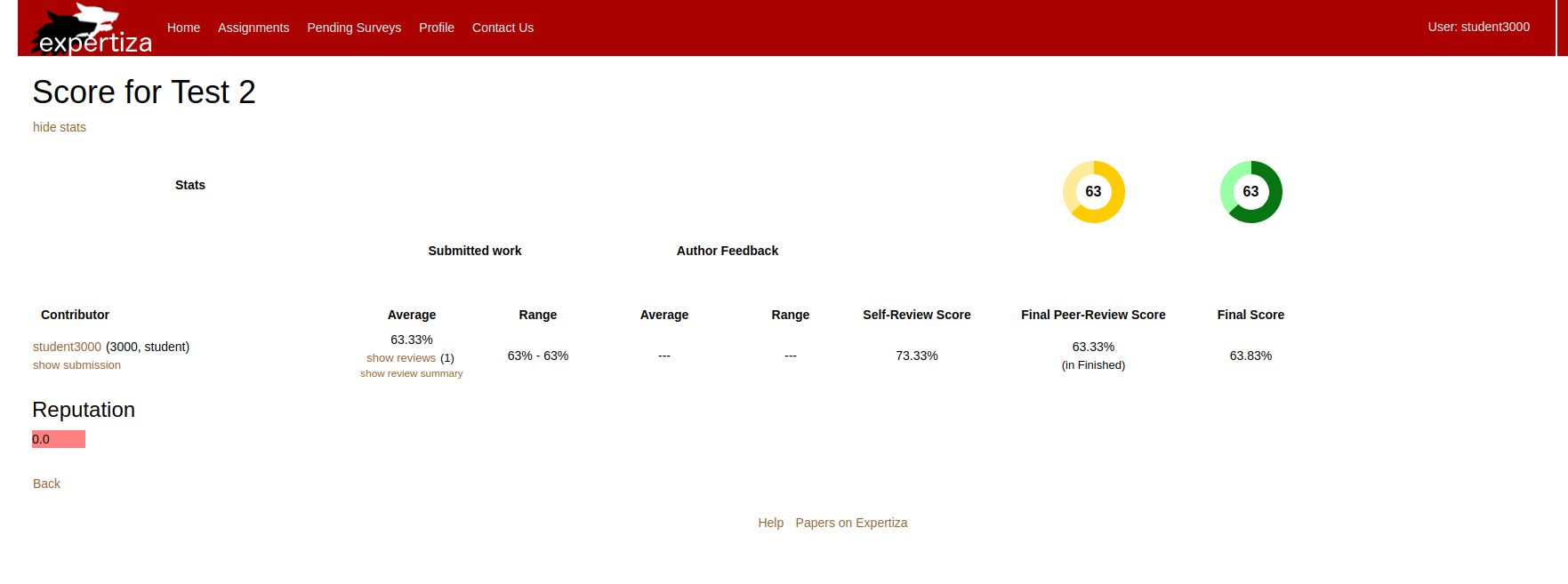
The following screenshot shows the final result of the code implementation. | |||
[[File:Selfreview final screenshot2.png|1150px]] | |||
'''Alternate View (view_my_scores)''' | |||
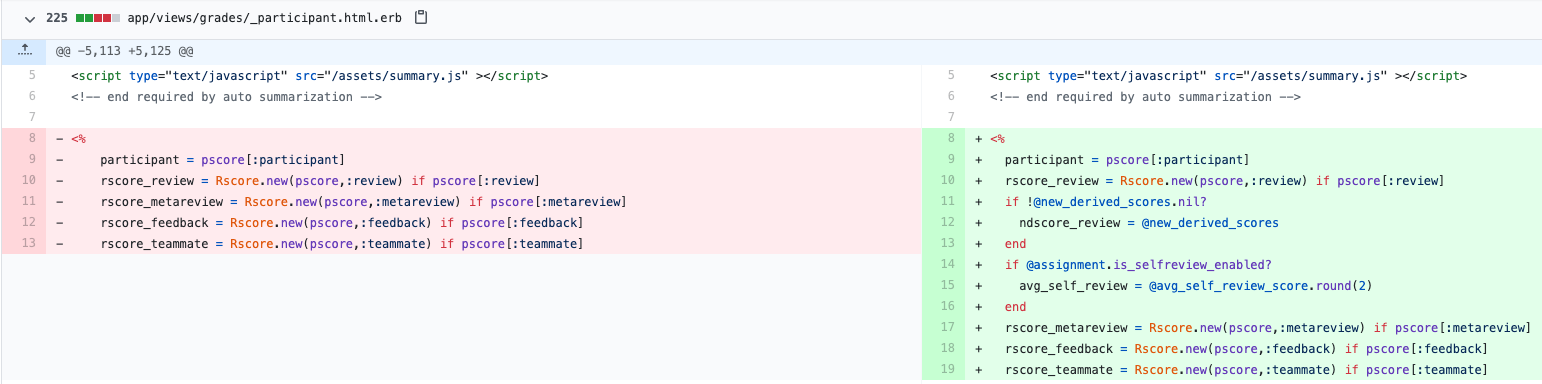
The _participant_*.html.erb files are responsible for the UI display of viewing assignment scores in the Alternate View. The following implementation shows the addition of the new columns for self-review score and the final composite score (along with a doughnut chart for the final score). | |||
[[File:selfreviews14.png|1200px]] | |||
[[File:selfreviews15.png|1200px]] | |||
The following screenshot shows the final result of the code implementation. | |||
[[File:Selfreview final screenshot1.png|1150px]] | |||
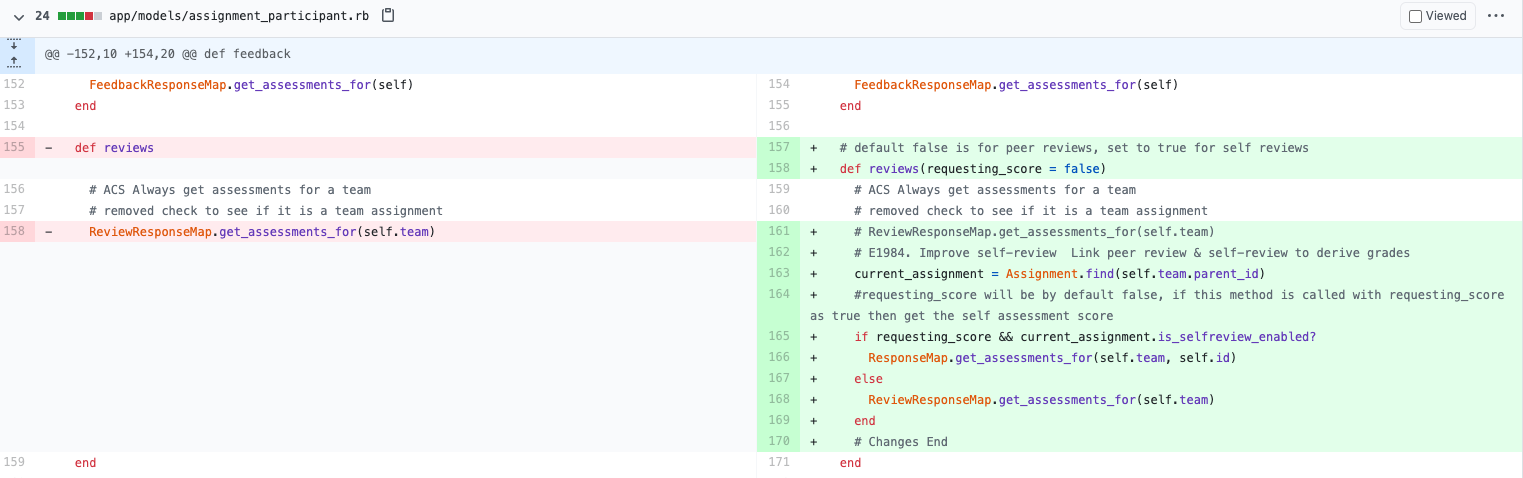
'''Response Map for Reviews''' | |||
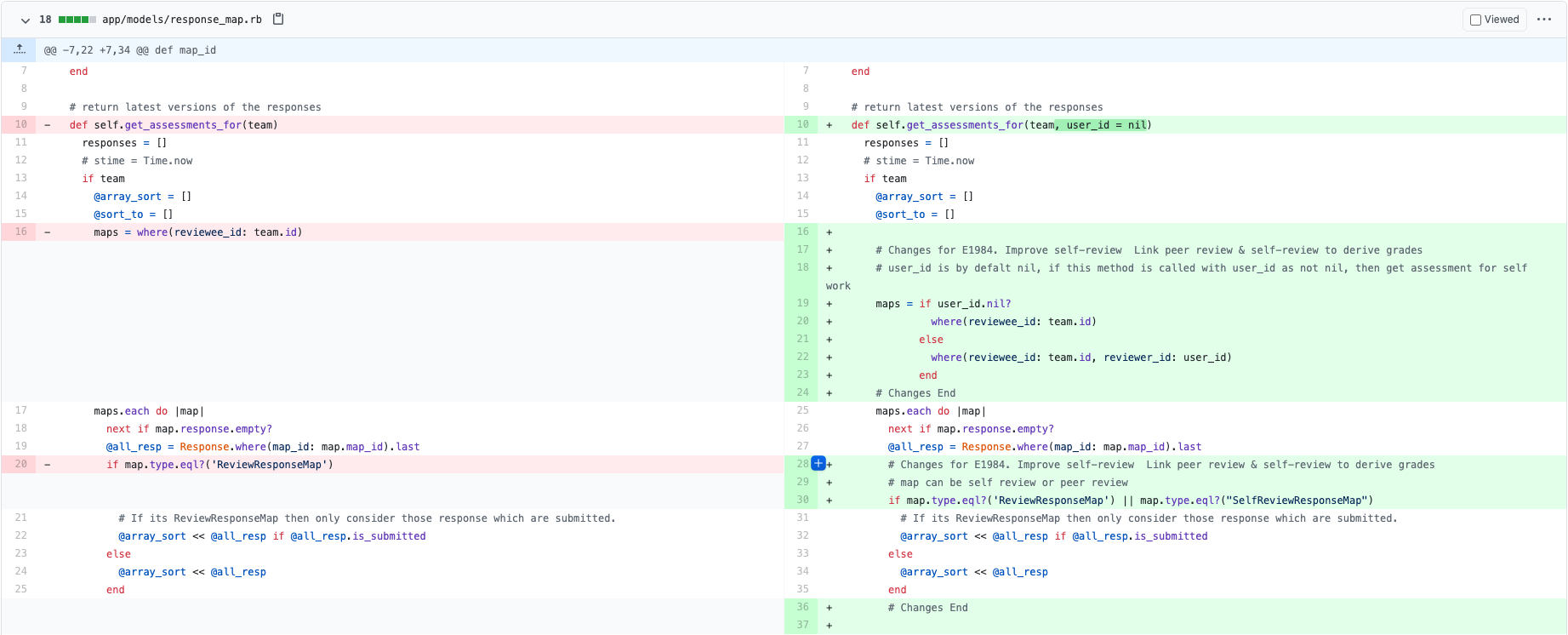
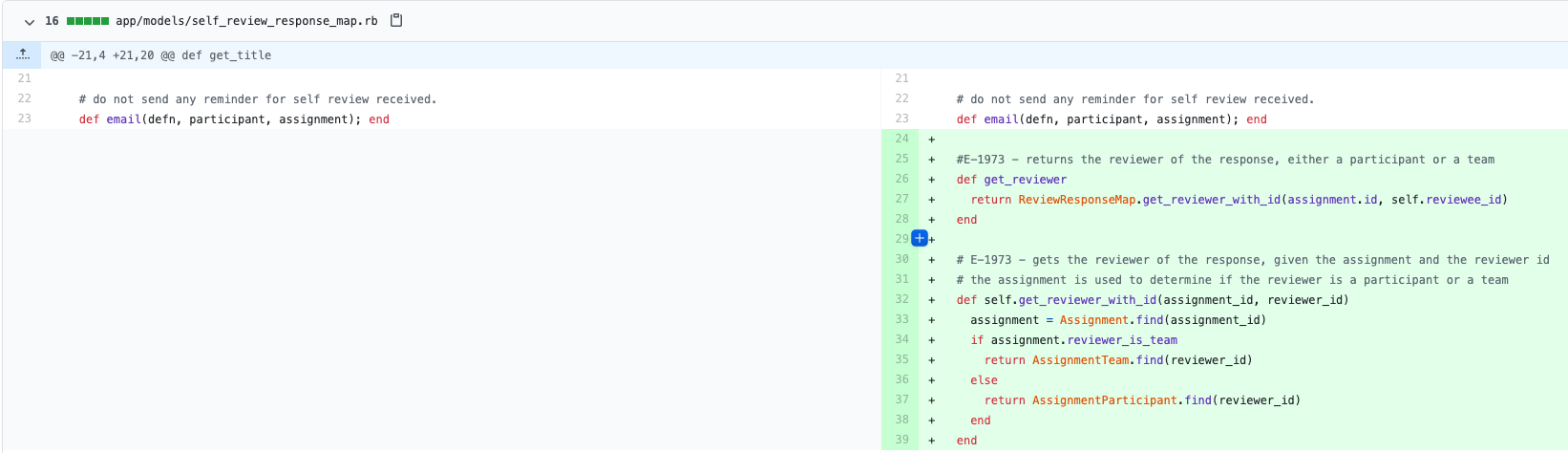
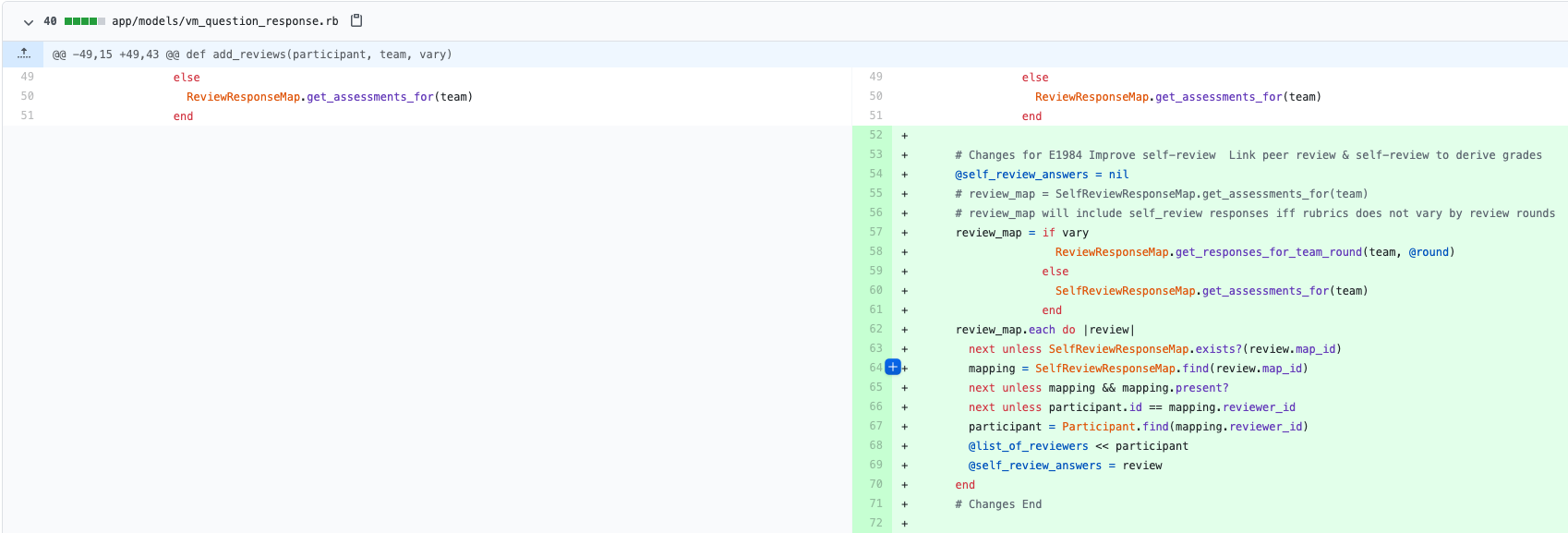
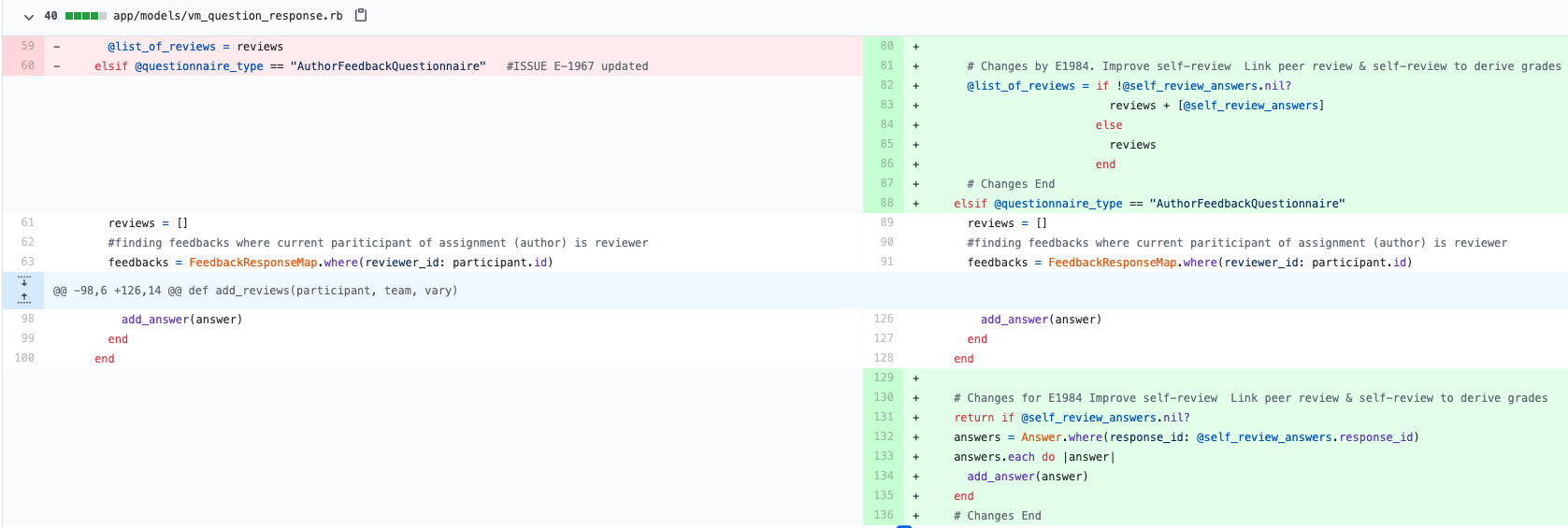
The following code implementations illustrate the response map additions for the response mapping. This is responsible for the functionality of conducting a self-review and gathering the results per assignment. | |||
[[File:selfreviews9.png|1200px]] | |||
[[File:selfreviews10.png|1200px]] | |||
[[File:selfreviews11.png|1200px]] | |||
[[File:selfreviews12.png|1200px]] | |||
=== Derive Composite Score === | |||
In the following screenshots we have implemented code in the grades_controller.rb to call upon helper functions in the grades_helper.rb that will compute the peer and self final score. The formula that will be chosen depends on which formula the instructor selects when they create the assignment. | |||
[[File:selfreviews1.png|1200px]] | |||
[[File:selfreviews2.png|1200px]] | |||
[[File:selfreviews3.png|1200px]] | |||
[[File:selfreviews4.png|1200px]] | |||
'''Instructor View for Reviews''' | |||
The following screenshot is the code that we implemented to allow a teacher to a which formula, in the UI, to use to account for self-reviews in the assignment review grading. | |||
[[File:selfreviews13.png|1200px]] | |||
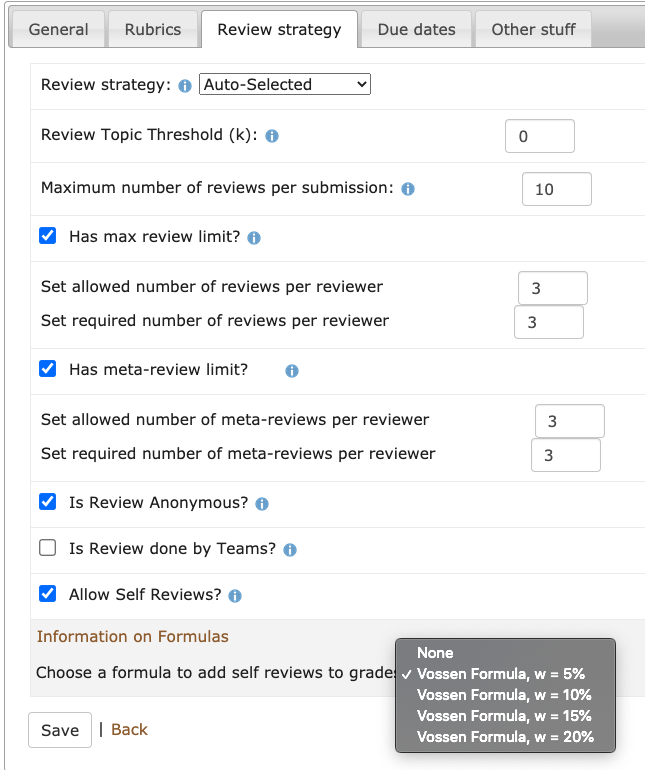
The screenshot of the interface below is the resulting UI from the code implementation above. | |||
[[File:selfreviews19.png|600px]] | |||
=== Implement Requirement to Review Self before Viewing Peer Reviews === | |||
The following screenshots are the files which we implemented booleans so that a student will not be able to see their scores unless they have filled out their self reviews. | |||
[[File:selfreviews5.png|1200px]] | |||
[[File:selfreviews6.png|1200px]] | |||
[[File:selfreviews7.png|1200px]] | |||
[[File:selfreviews8.png|1200px]] | |||
== Test Plan == | == Test Plan == | ||
Our project will utilize various testing techniques. These methods of testing involve manual testing (black box testing) and RSpec testing (white box testing). | |||
=== Manual Testing === | === Manual Testing === | ||
'''Credentials''' | |||
*username: ''instructor6'', password: ''password'' | |||
*username: ''student3000'', password: ''password'' | |||
*username: ''student4000'', password: ''password'' | |||
The steps outlined for manual testing will become clearer upon implementation, but the proposed plan is the following: | |||
==== Prerequisite Steps ==== | |||
=== | :1. Log in to the development instance of Expertiza as an ''instructor6'' | ||
:2. Create an assignment that allows for self-reviews. To allow for self-reviews, check the box "Allow Self-Reviews" in the Review Strategy tab. | |||
::2.1. Make sure the submission deadline is after the current date and time | |||
::2.2. Likewise, the review deadline should then be greater than the submission deadline | |||
:3. Add ''student3000'' and ''student4000'' to the newly created assignment (i.e. "Test Assignment") | |||
==== Must Review Self before Viewing Peer Reviews ==== | |||
This test will assure that the logged in user cannot view their peer-reviews for a given assignment unless they have performed a self-review. | |||
:1. Sign as ''student3000'' | |||
::1.1. Submit any file or link to the new Test Assignment | |||
:2. Log back in as the ''instructor6'' | |||
::2.1. Edit the Test Assignment to change the submission date to be in the past, enabling peer reviews | |||
:3. Log in as ''student3000'' | |||
:4. Attempt to view peer-review scores by clicking on "Your Scores" within the Test Assignment. This button should be disabled | |||
:5. Log back in as the ''instructor6'' | |||
::5.1. Edit the Test Assignment to change back the submission date to be in the future | |||
:6. Log in as ''student3000' | |||
::6.1. Perform a self-review | |||
:7. Log back in as the ''instructor6'' | |||
::7.1. Edit the Test Assignment to change the submission date to be in the past, enabling peer reviews | |||
:8. Log in as ''student3000' | |||
::8.1. Go view peer-review scores by clicking on "Your Scores". This button should now be enabled | |||
==== Viewing Self Review Score Juxtaposed with Peer Review Scores ==== | |||
This test confirms that the the students self-review scores are displayed with peer-review scores. It additionally confirms that self-review scores are considered in the review grading with the calculation of a composite score. | |||
:1. Sign as ''student3000'' | |||
::1.1. Submit any file or link to the new Test Assignment | |||
::1.2. Perform a self-review | |||
:2. Repeat step 1 ''student4000'' | |||
:3. Log back in as the ''instructor6'' | |||
::3.1. Edit the Test Assignment to change the submission date to be in the past, enabling peer reviews | |||
:4. Log back in as ''student4000'' | |||
::4.1. Perform a peer-review on the submission from ''student3000'' | |||
:5. Log in as ''student3000'' | |||
:6. Go view peer-review scores by clicking on "Your Scores". | |||
::6.1. Assure that there is a column for self-review scores | |||
::6.2. Confirm there is a composite score calculation underneath the average peer review score. | |||
:7. Go back to the assignment view. Click "Alternate View" | |||
::7.1. Confirm that there is a new column illustrating the self-review average | |||
::7.2. Confirm that there is a column in the grades table displaying composite score (Final score) | |||
::7.3. Check is there is a doughnut chart displaying the composite score (Final score) | |||
=== RSpec Testing === | |||
We plan to implement new RSpec tests to verify our implementations of the composite score calculation and the requirement to self-review first. Once written, we will be able to go more in-depth on the details of our testing. | |||
==== Test Composite Score Derivation ==== | |||
The following screenshot is an rspec test that we added in the grades_helper_spec.rb file. This tested to see if the Vossen formula that we implemented would output the correct score when given a average peer, average self review score, weight, and leniency. | |||
[[File:selfreviews20.png|1200px]] | |||
== Relevant Links == | == Relevant Links == | ||
| Line 145: | Line 323: | ||
'''Our repository''': https://github.com/jhnguye4/expertiza/tree/beta | '''Our repository''': https://github.com/jhnguye4/expertiza/tree/beta | ||
'''Pull request''': | '''Pull request''': https://github.com/expertiza/expertiza/pull/1831 | ||
'''Video demo''': | '''Video demo''': https://www.youtube.com/watch?v=BYnhUNOTejs | ||
== References == | == References == | ||
| Line 154: | Line 332: | ||
[https://github.com/expertiza/expertiza/pull/1611 E1984 Pull Request] | [https://github.com/expertiza/expertiza/pull/1611 E1984 Pull Request] | ||
[https://expertiza.csc.ncsu.edu/index.php/CSC/ECE_517_Fall_2019_-_E1984._Improve_self-review_Link_peer_review_&_self-review_to_derive_grades E1984 wiki] | |||
Latest revision as of 17:38, 15 November 2020
Project Overview
In Expertiza, it is currently possible to check the “Allow self-review” box on the Review Strategy tab of assignment creation, and then an author will be asked to review his/her own submission in addition to the submissions of others. But as currently implemented, nothing is done with the scores on these self-reviews.
There has been a previous attempt at solving this problem, but there were several issues with that implementation:
- The formula for weighting self-reviews is not modular. It needs to be, since different instructors may want to use different formulas, so several should be supported.
- There are not enough comments in the code.
- It seems to work for only one round of review.
View documentation for previous implementation here.
Objectives
Our objectives for this project are the following:
- Display the self-review score with peer-review scores for the logged in user
- Implement a way to achieve a composite score with the combination of the self-review score and peer-review scores
- Implement a requirement for the logged in user to self-review before viewing peer-reviews
- Assure that we overcome the issues outlined for the previous implementation of this project
Team
Courtney Ripoll (ctripoll)
Jonathan Nguyen (jhnguye4)
Justin Kirschner (jkirsch)
Files Involved
Back-end
- app/controllers/grades_controller.rb
- app/helpers/grades_helper.rb
- app/models/assignment_participant.rb
- app/models/author_feedback_questionnaire.rb
- app/models/response_map.rb
- app/models/review_questionnaire.rb
- app/models/self_review_response_map.rb
- app/models/teammate_review_questionnaire.rb
- app/models/vm_question_response.rb
Front-end
- app/views/assignments/edit/_review_strategy.html.erb
- app/views/grades/_participant.html.erb
- app/views/grades/_participant_charts.html.erb
- app/views/grades/_participant_title.html.erb
- app/views/grades/view_team.html.erb
Testing
- spec/models/assignment_particpant_spec.rb
- spec/controllers/grades_controller_spec.rb
Use Case for Self-Assessment
The following diagram illustrates how the self-assessment feature should work between student and instructor within Expertiza. In summary, an instructor can create an assignment and enable self-review. A student can then submit to the assignment creates by the instructor and provide a self-review. Only then can the student view all of their review scores.
Design Plan for Tasks
Display Self-Review Scores w/ Peer-Reviews
It should be possible to see self-review scores juxtaposed with peer-review scores. Design a way to show them in the regular "View Scores" page and the alternate (heat-map) view. They should be shown amidst the other reviews, but in a way that highlights them as being a different kind of review.
Design Plan
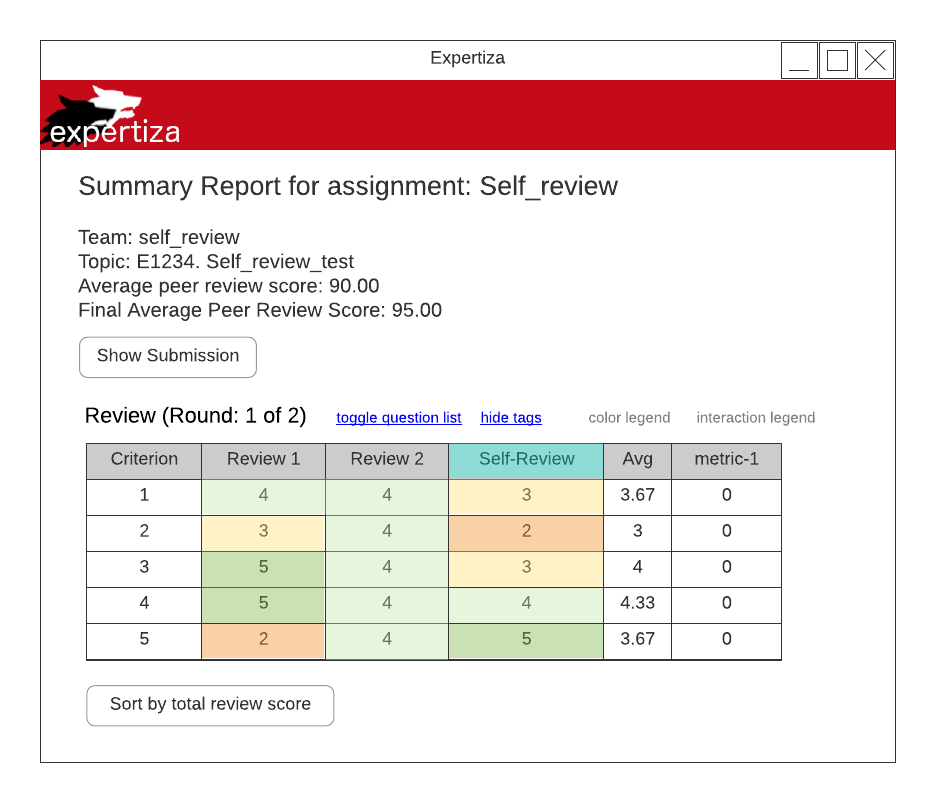
In the current implementation of Expertiza, students can view a compilation of all peer review scores for each review question and an average of those peer-reviews. For our project, we plan to add the self-review score alongside the peer-review scores for each review question. In the wire-frame below, note that for each criterion there is a column for each peer-review score and a single column for the self-review score. Currently implemented in the system, the avg column takes an average of all the review scores. These scores (peer-reviews average and self-review) will be used to determine the overall composite score for the team's reviews. Furthermore, the average composite score is displayed on the page under the average peer review score, labeled "Final Average Peer Review Score". How we plan to derive a composite score is explained in detail in the follow section Derive Composite Score.
In the alternate view, our plan does not alter the current interface too much. The only addition we plan to implement is additional columns for the self-review average and for the composite (final) score a student has received for an assignment. Likewise, there is now an additional doughnut chart providing a visual of the composite score (green) alongside the final review score (yellow).
Note: The diagrams above are wireframes. The values displayed are not be taken literally, they are for design purposes only.
Derive Composite Score
Implement a way to combine self-review and peer-review scores to derive a composite score. The basic idea is that the authors get more points as their self-reviews get closer to the scores given by the peer reviewers. So the function should take the scores given by peers to a particular rubric criterion and the score given by the user. The result of the formula should be displayed in a conspicuous page on the score view.
The formula we use to determine a final grade from, 1) the peer reviews and 2) how closely self reviews match the peer reviews, uses a type of additive scoring rule, which computes a weighted average between team score (peer reviews) and student rating (self review). More specifically, it uses a type of mixed additive-multiplicative scoring rule, which multiplies student score (self review) by a function of the team score (peer reviews), and adds its weighted version to the weighted peer review score. This is also known as 'assessment by adjustment'. The formula is a practical scoring rule for additive scoring with unsigned percentages (grades from 0%-100%).
The pseudo-code for a function that implements the formula is as follows:
function(avg_peer_rev_score, self_rev_score, w)
grade = w*(avg_peer_rev_score) + (1-w)*(SELF)
where:
SELF = avg_peer_review_score * (1 - (|avg_peer_review_score - self_review_score|/avg_peer_review_score))
and where: avg_peer_review_score is simply the mechanism already existing in Expertiza for assigning a grade from peer review scores.
and where: w - weight - (0 <= w <= 1) is the inverse proportion of how much of the final grade is determined by the closeness of the self review to the average of the peer reviews (w is the proportion of the grade to be determined by the original grade determination: the peer review scores).
An example:
- The average peer review score is 4/5, the self review score is 5/5.
- The instructor chooses w to equal 0.95, so that 5% of the grade is determined from the deviation of the self review from the peer reviews.
The final grade, instead of being the peer review score of 4/5 (80%) is now: 0.95*(4/5) + 0.05*(4/5*(1-|4/5-5/5|/(4/5))) = 79%. If the instructor chose w to equal 0.85 (instead of 0.95), the grade is 77% (instead of 79%) because deviation from peer reviews is a larger weighted value of the final grade.
The above is a basic version of the grading formula. It is basic in that it only allows deviations of the self review scores from the peer review scores to result in a decrease in the final grade and a deviation will always result in a decrease of the final grade. We propose another parameter to the formula, l - leniency, as another way (in addition to w - weight) for the instructor to modularly determine the final grade for an assignment. The parameter l - leniency - can determine a threshold by which the final grade will account/adjust for self reviews' deviations from peer reviews only when the deviation reaches this threshold (measured in percentage deviation from the average peer review). If the difference does not meet the threshold, no penalty will be subtracted from the peer review. In addition, if the difference does not meet the threshold (the self review score is sufficiently close to the peer review scores), the instructor can choose to add points to final grade based on the magnitude of the difference. Since the formula is a mixed additive-multiplicative scoring rule (mentioned above), the instructor needs to simply pick l - leniency - as a percentage (similar to the functionality of w).
To recap: w should be chosen based on the instructor's desired percentage (w) of the final grade to be determined from peer reviews and, conversely, the instructor's desired percentage (1-w) of the final grade to be determined by the extent to which self reviews deviate from peer reviews. In addition, l - leniency, should be chosen based on the instructor's desired percentage of the deviation of self review from peer review that could result in no grade deduction from the deviation if the deviation is sufficiently small (or even a grade increase if the instructor wants to increase the score of individuals with a small deviation).
The following is pseudo-code for if an instructor wishes to not subtract from the final grade if the deviation is sufficiently small. Notice that the leniency condition, the instructor's desired percentage of the deviation of self review from peer review, is naturally part of the grading formula in SELF:
if |avg_peer_review_score - self_review_score|/avg_peer_review_score <= l(leniency)
grade = avg_peer_review_score
else
run formula
In addition. instead of assigning a final grade equal to the avg_peer_review_score if the leniency condition is met, the grade can be adjusted (increased) if the instructor wishes to do so, since the self review is sufficiently close (determined by l) to the peer reviews. The formula for determining the final grade would thus add the small extent of deviation to the final grade rather than subtracting it (in SELF, 1 - ..., is changed to 1 + ...):
function(avg_peer_rev_score, self_rev_score, w)
grade = w*(avg_peer_rev_score) + (1-w)*(SELF)
where:
SELF = avg_peer_review_score * (1 + (|avg_peer_review_score - self_review_score|/avg_peer_review_score))
In this case, the pseudo-code is:
if |avg_peer_review_score - self_review_score|/avg_peer_review_score <= l(leniency)
grade = w*(avg_peer_rev_score) + (1-w)*(avg_peer_review_score * (1 + (|avg_peer_review_score - self_review_score|/avg_peer_review_score)))
else
grade = w*(avg_peer_rev_score) + (1-w)*(avg_peer_review_score * (1 - (|avg_peer_review_score - self_review_score|/avg_peer_review_score)))
Using the previous example (average peer review score is 4/5, self review score is 5/5, w = 0.95), the self review score (5/5) differs by 25% of the peer review score (4/5). In other words, |avg_peer_review_score - self_review_score|/avg_peer_review_score = 1/4 = 25%. Based on l - leniency, the instructor can decide:
- 1. if a 25% deviation is sufficiently large to warrant penalizing the final grade by (1-w)*(SELF) (so that the final grade is 79%, instead of 80%).
- 2. if a 25% deviation is sufficiently small to warrant keeping the final grade as grade = avg_peer_review_score, with no penalty for the deviation (so that the grade is 80%)
- 3. if a 25% deviation is sufficiently small to warrant increasing the final grade by (1-w)*(SELF), where the SELF formula contains a 1 + ..., instead of a 1 - ... (so that the grade is 81%)
Implementation Plan
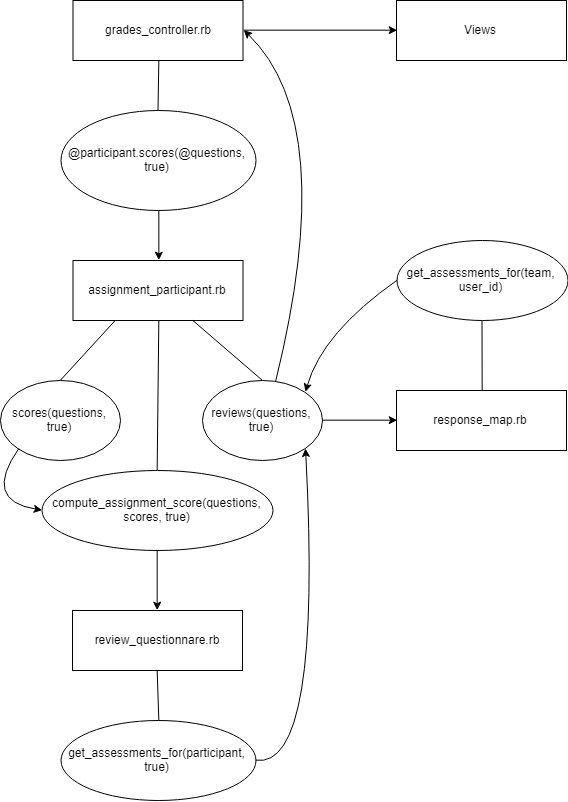
In order to incorporate the combined score into grading, we will change the logic in grades_controller.rb, which implements the grading formula. We will remove most of the code from the previous implementation since the formula/method used is unsatisfactory. With the new grading formula, the grades_controller can assign a final grade by following these steps:
- 1. We can obtain the peer review ratings and the score/grade derived from them by calling scores(), which then calls compute_assignment_score(), both from the assignment_participant.rb model. In order to compute the assignment score, compute_assignment_score() calls another method named get_assessments_for(), which is located in review_questionnare.rb model.
- 2. The get_assessments_for() method will call the reviews() method, also located in assignment_participant.rb.
- 3. Finally, the reviews() method will get the scores by simply calling the get_assessments_for() method located in the response_map.rb model.
- 4. Once the scores have been retrieved by using the various model methods, the controller can use the scores to calculated a final grade by using the formula. This grade is then passed to the view.
Below is a flow diagram for how grades_controller.rb, which implements the grading formula (as mentioned in the first step) and presents the grade in the view (top of the diagram). Note: The self-review scores are obtained by using the true parameter in all the methods calls (as shown in the diagram), whereas the peer-review scores are retrieved similarly but omitting this parameter.
Implement Requirement to Review Self before Viewing Peer Reviews
There would be no challenge in giving the same self-review scores as the peer reviewers gave if the authors could see peer-review scores before they submitted their self-reviews. The user should be required to submit their self-evaluation(s) before seeing the results of their peer evaluations.
Implementation Plan
By being able to self review before peer review, it allows the author of the assignment to have an unbiased opinion on the quality of work they are submitting. When the judgement of their work is not influenced by others who have given feedback, they are able to get a clearer view of the strengths and weaknesses of their assignment. Self reviews before peer reviews can also be more beneficial to the user as it can show if the user has the correct or wrong approach to their solution compared to their peers.
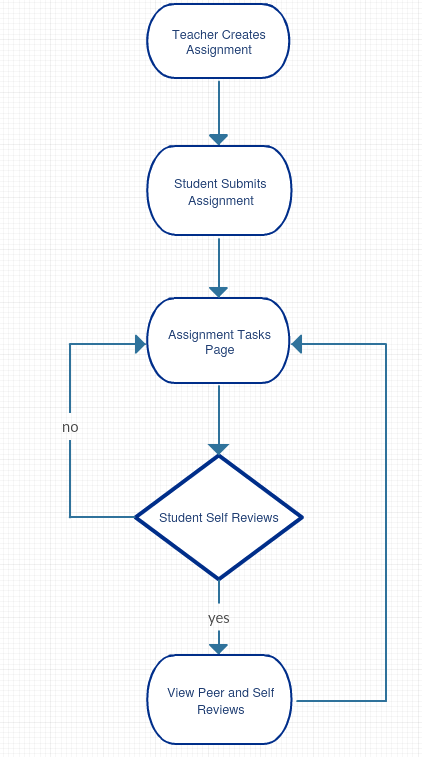
In the current implementation of self review, the user is able to see the peer reviews before they have made their own self review. The reason that this is occurring is due to the fact that when the user goes to see their scores, the page is not checking that a self review has been submitted. In order to fix this issue, we will add a boolean parameter to self review and pass it to viewing pages where it is called. When a user is at the student tasks view, the "Your scores" link will be disabled if the user has not filled out their self review. If the user has filled out their self review, then he/she will be redirected to the Display Self-Review Scores with Peer-Reviews page.
Below is a control flow diagram for how a student will be able to view their peer and self review score.
Implementation of Design Plan
Display Self-Review Scores w/ Peer-Reviews
The following code and UI screenshots illustrate the implementation of displaying the self-review scores alongside the peer-reviews. This also includes displaying the final score that aggregates the self-review score utilizing a chosen formula. The final score derivation process is described in the Derive Composite Score task.
View Team Review Scores (view_team)
The view_team.html.erb file is responsible for the display of the peer-review scores heat map. In this implementation, we added a display for the Final Average Peer Review Score, which is the score that takes the average self-review score into consideration based on a set formula. Additionally, there is now a self-review score column (highlighted in cyan) that displays the self-review score for each criterion alongside the peer-review given.
The following screenshot shows the final result of the code implementation.
Alternate View (view_my_scores)
The _participant_*.html.erb files are responsible for the UI display of viewing assignment scores in the Alternate View. The following implementation shows the addition of the new columns for self-review score and the final composite score (along with a doughnut chart for the final score).
The following screenshot shows the final result of the code implementation.
Response Map for Reviews
The following code implementations illustrate the response map additions for the response mapping. This is responsible for the functionality of conducting a self-review and gathering the results per assignment.
Derive Composite Score
In the following screenshots we have implemented code in the grades_controller.rb to call upon helper functions in the grades_helper.rb that will compute the peer and self final score. The formula that will be chosen depends on which formula the instructor selects when they create the assignment.
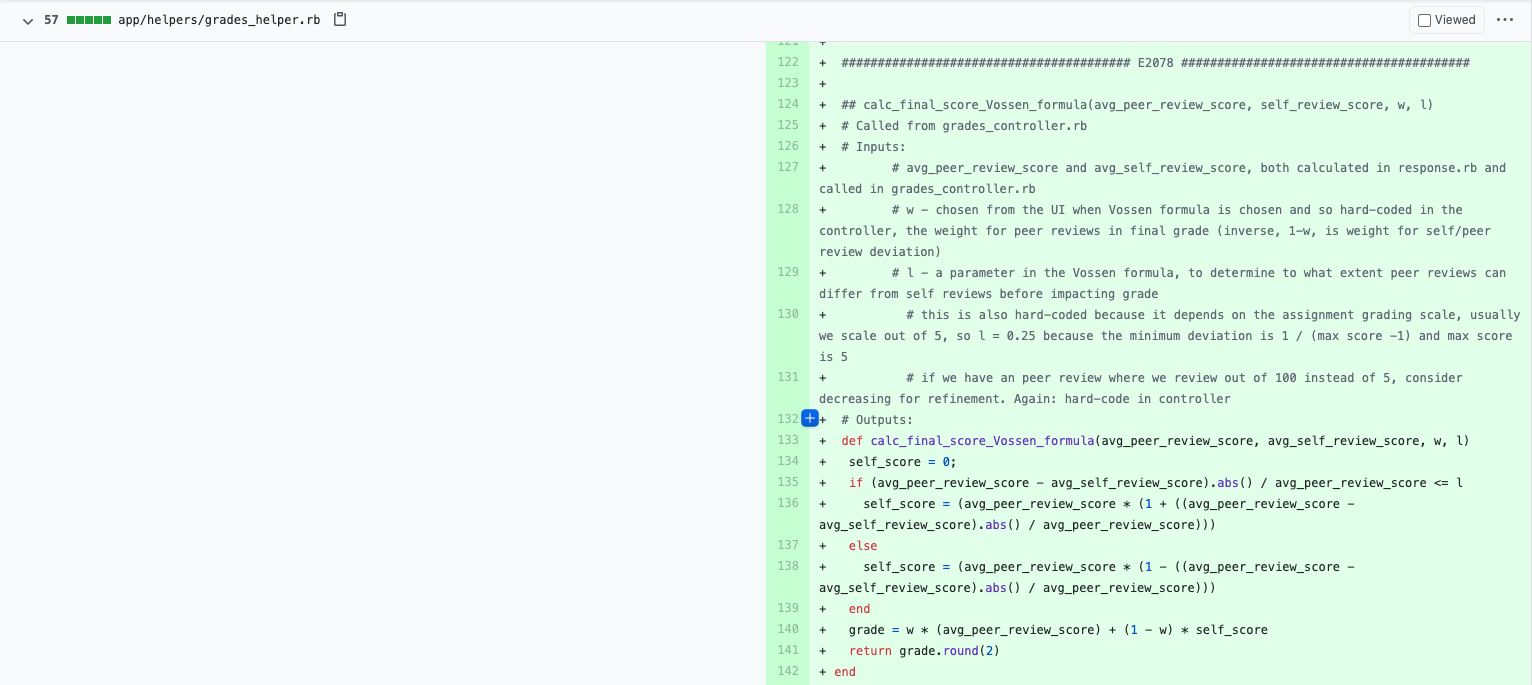
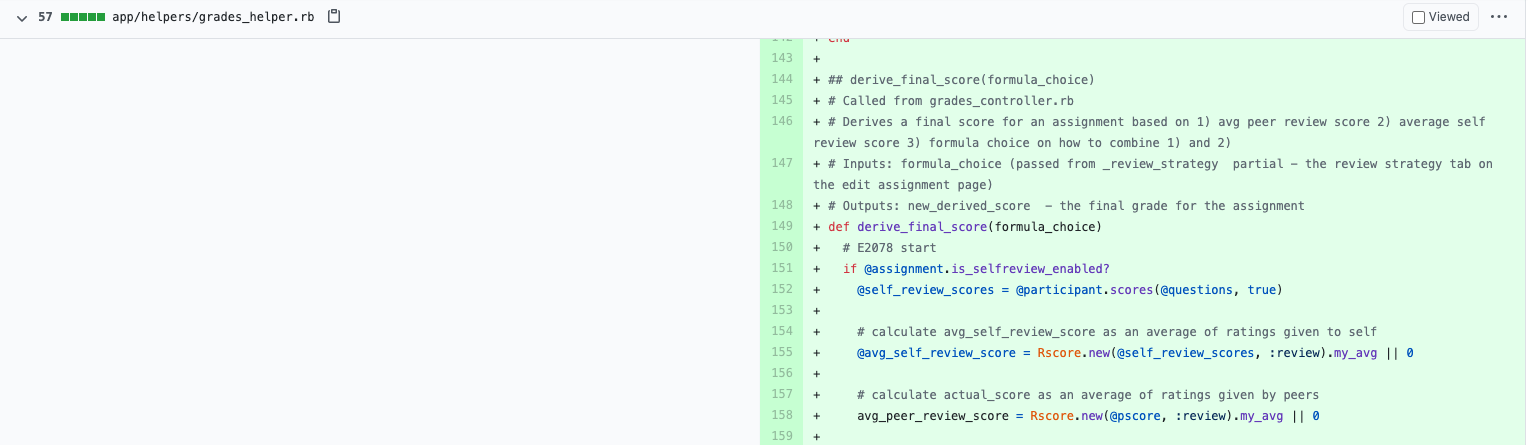
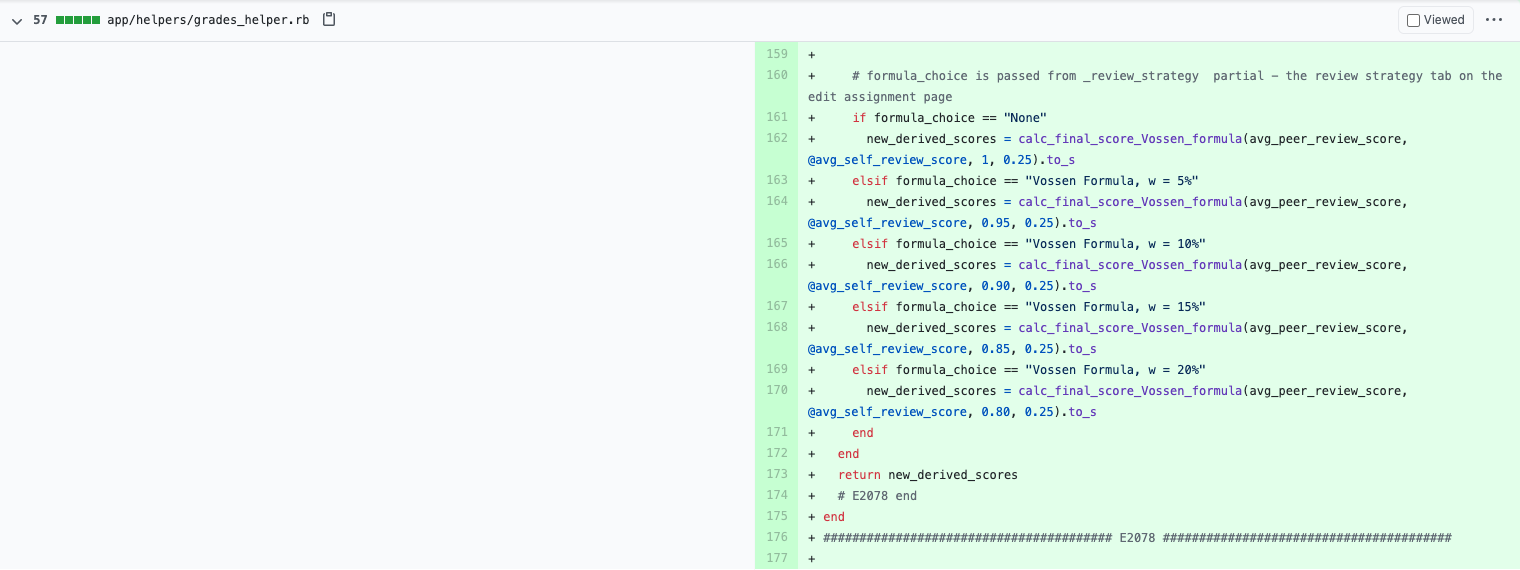
Instructor View for Reviews
The following screenshot is the code that we implemented to allow a teacher to a which formula, in the UI, to use to account for self-reviews in the assignment review grading.
The screenshot of the interface below is the resulting UI from the code implementation above.
Implement Requirement to Review Self before Viewing Peer Reviews
The following screenshots are the files which we implemented booleans so that a student will not be able to see their scores unless they have filled out their self reviews.
Test Plan
Our project will utilize various testing techniques. These methods of testing involve manual testing (black box testing) and RSpec testing (white box testing).
Manual Testing
Credentials
- username: instructor6, password: password
- username: student3000, password: password
- username: student4000, password: password
The steps outlined for manual testing will become clearer upon implementation, but the proposed plan is the following:
Prerequisite Steps
- 1. Log in to the development instance of Expertiza as an instructor6
- 2. Create an assignment that allows for self-reviews. To allow for self-reviews, check the box "Allow Self-Reviews" in the Review Strategy tab.
- 2.1. Make sure the submission deadline is after the current date and time
- 2.2. Likewise, the review deadline should then be greater than the submission deadline
- 3. Add student3000 and student4000 to the newly created assignment (i.e. "Test Assignment")
Must Review Self before Viewing Peer Reviews
This test will assure that the logged in user cannot view their peer-reviews for a given assignment unless they have performed a self-review.
- 1. Sign as student3000
- 1.1. Submit any file or link to the new Test Assignment
- 2. Log back in as the instructor6
- 2.1. Edit the Test Assignment to change the submission date to be in the past, enabling peer reviews
- 3. Log in as student3000
- 4. Attempt to view peer-review scores by clicking on "Your Scores" within the Test Assignment. This button should be disabled
- 5. Log back in as the instructor6
- 5.1. Edit the Test Assignment to change back the submission date to be in the future
- 6. Log in as student3000'
- 6.1. Perform a self-review
- 7. Log back in as the instructor6
- 7.1. Edit the Test Assignment to change the submission date to be in the past, enabling peer reviews
- 8. Log in as student3000'
- 8.1. Go view peer-review scores by clicking on "Your Scores". This button should now be enabled
Viewing Self Review Score Juxtaposed with Peer Review Scores
This test confirms that the the students self-review scores are displayed with peer-review scores. It additionally confirms that self-review scores are considered in the review grading with the calculation of a composite score.
- 1. Sign as student3000
- 1.1. Submit any file or link to the new Test Assignment
- 1.2. Perform a self-review
- 2. Repeat step 1 student4000
- 3. Log back in as the instructor6
- 3.1. Edit the Test Assignment to change the submission date to be in the past, enabling peer reviews
- 4. Log back in as student4000
- 4.1. Perform a peer-review on the submission from student3000
- 5. Log in as student3000
- 6. Go view peer-review scores by clicking on "Your Scores".
- 6.1. Assure that there is a column for self-review scores
- 6.2. Confirm there is a composite score calculation underneath the average peer review score.
- 7. Go back to the assignment view. Click "Alternate View"
- 7.1. Confirm that there is a new column illustrating the self-review average
- 7.2. Confirm that there is a column in the grades table displaying composite score (Final score)
- 7.3. Check is there is a doughnut chart displaying the composite score (Final score)
RSpec Testing
We plan to implement new RSpec tests to verify our implementations of the composite score calculation and the requirement to self-review first. Once written, we will be able to go more in-depth on the details of our testing.
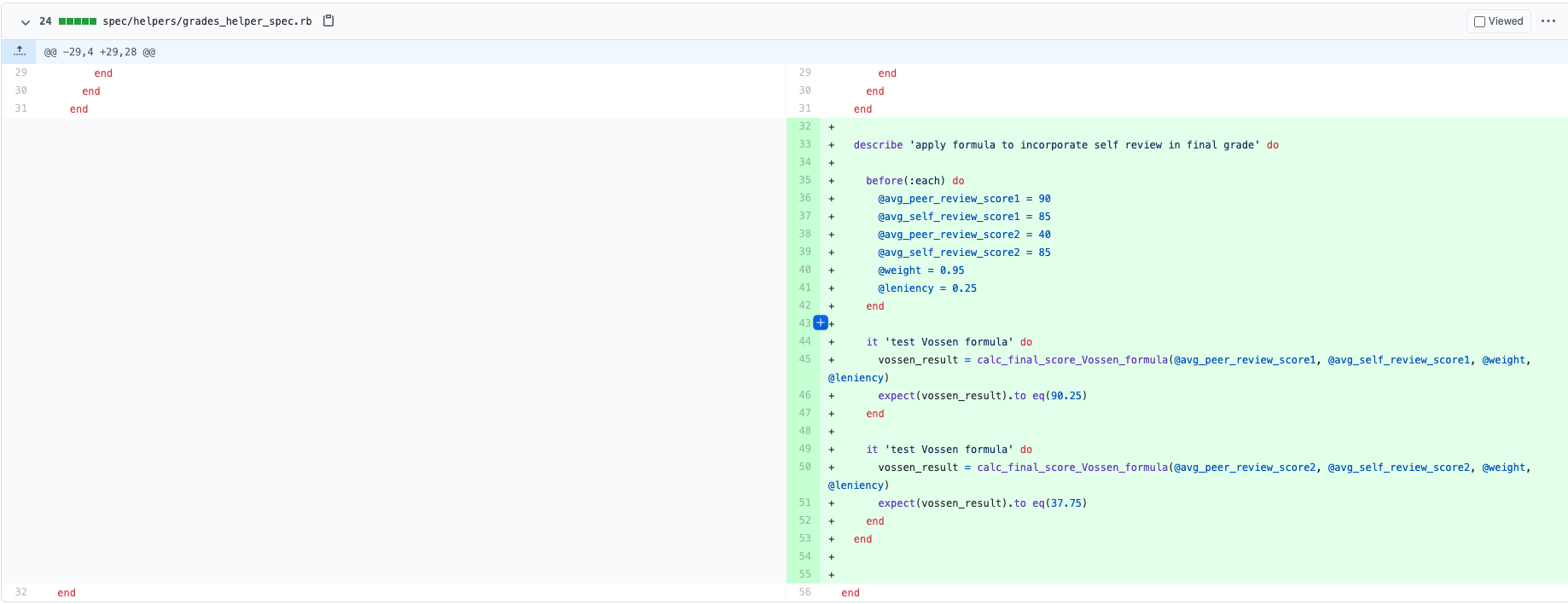
Test Composite Score Derivation
The following screenshot is an rspec test that we added in the grades_helper_spec.rb file. This tested to see if the Vossen formula that we implemented would output the correct score when given a average peer, average self review score, weight, and leniency.
Relevant Links
Our repository: https://github.com/jhnguye4/expertiza/tree/beta
Pull request: https://github.com/expertiza/expertiza/pull/1831
Video demo: https://www.youtube.com/watch?v=BYnhUNOTejs
References
Scoring models for peer assessment in team-based learning projects